선택조립방식의 효율성에 대한 시뮬레이션 검토
Abstract
Purpose
This paper compares the effectiveness of typical selective assembly criteria and suggests the most promising one. Based on the result of a computer simulation, the key issues of selective assembly are examined and the best criterion is recommended from the effectiveness perspective.
Methods
Using JAVA program, production of ten thousand units for each pair of components are simulated for selective assembly of the two types. And the number of mismatching and the fraction nonconforming for each criterion are determined.
Results
The best match criterion appeared to be most promising from the perspectives of both mismatching and nonconforming problems. Its effectiveness appears to be also good even when the precision of one component is different from that of the other.
Conclusion
For designing an optimal method for selective assembly, the best match criterion is recommend-able as the base criterion.
Key words: Selective Assembly, Dimensional Partitioning, Best Matching, Ordered Matching
1. 서 론
선택조립방식은 두 개의 핵심부품을 조립하여 완성되는 제품을 생산할 때 많이 사용되는 제조기법이다. 자동차 엔진이나 연료분사장치 등 제품에 요구되는 가공 정밀도가 높을 경우, 공차의 누적 현상까지 고려하여 요구정밀도를 충족하려면 부품의 가공치수가 극히 정밀해야만 한다. 그러나 치수의 정밀도 향상을 위해서는 기하급수적으로 상승하는 원가 부담을 감수해야 하므로 제품의 가격경쟁력 확보에 지장을 초래하게 된다. 이와 같은 문제를 경제적으로 해결하는 방안으로 산업현장에서는 선택조립방식이 많이 활용되어 왔다. 즉, 일단 생산된 두 종류의 부품을 치수에 따라 적절하게 몇 개의 범주로 분류한 후, 같은 범주에 속한 부품끼리 조립함으로써 조립된 제품 치수의 정밀도를 향상시키는 것이다. 이와 같은 방식은 조립 후 피스톤과 실린더 사이의 간격이 성능에 크게 영향을 주는 내연엔진이나 바디와 니들의 틈이 성능에 영향을 주는 연료분사장치 등의 생산에 널리 사용된다. 선택조립은 상대적으로 정밀도가 떨어지는 부품가공공정이라 하더라도 높은 정밀도의 조립품 생산이 가능하게 해준다. 그러나 선택조립방식을 취할 경우 두 부품의 상응하는 범주에 같은 수량의 부품이 있다는 보장이 없으므로 미조립부품의 문제가 수반되게 된다. 이와 같은 문제는 두 부품 치수의 표준편차에 차이가 있으면 더욱 심각하게 된다.
그동안 산업현장에서는 선택조립 유형별로 여러 연구결과가 있었음에도 불구하고 주로 치수분할방식이 사용되어 왔다. 이것은 측정과 비교를 통해 조립할 부품 쌍을 선택하는 통계적 선택조립 방식이 생산지연을 초래할 수 있기 때문으로 사료된다. 그러나 4차 산업시대가 도래하면서 센서기술, 데이터 통신 기술, 컴퓨터 연산능력 등의 획기적인 향상으로 선택조립 방식의 차이에 따른 생산지연 문제가 해소되게 되었다. 따라서 4차 산업 환경 하에서의 선택조립 문제는 여러 방식들 중 어느 모형이 적합할 것인지 결정하여 생산현장에 구현하는 것이라 하겠다. 본 연구에서는 이와 같은 현실을 고려하여 선택조립의 산업현장 적용에 도움을 주고자 기존의 여러 연구들을 적절하게 분류하여 비교 및 분석하였다. 산업현장에서는 대부분 쌍을 이룬 두 부품으로 구성된 조립제품에 대해서만 선택조립방식을 적용하고 있으므로 연구 범위도 이 경우에 국한하였다. 또한 선택조립은 망목특성을 정밀하게 구현하고자 사용되는 제조공법이므로 부품 품질특성은 정규분포를 따른다고 가정하였다. 또한 부품 특성이 정규분포라고 하더라도 선택조립이 적용된 제품 특성은 정규분포를 따르지 않을 뿐만 아니라 극히 복잡한 형태의 분포가 되므로 시뮬레이션을 통해 데이터를 생성하여 비교 및 분석을 실시하였다. 대표적인 선택조립 방식들의 비교 기준으로 조립 정밀도 향상이라는 기본 목적 달성 정도와 선택조립에 수반되는 잉여부품 혹은 미조립 부품 문제 발생정도를 검토하고 가장 유망한 방식이 무엇인지 제시하였다. 본 논문의 2절에서는 선택조립방식을 분류하여 각 유형별로 개념과 절차를 소개한다. 3절에서 두 부품의 가공정밀도가 같을 경우에 대해 시뮬레이션의 시행방법과 각 유형별 결과를 제시한 후, 4절에서는 두 부품의 가공정밀도가 다를 경우로 확대하여 선택조립의 잉여부품 문제와 조립품 정밀도 향상 문제를 분석하였다. 5절에서 결과를 종합 요약하고 결론을 맺는다.
2. 선택조립방식의 유형
2.1 선택조립의 분류
산업현장에서 선택조립방식은 대부분 쌍을 이루는 두 부품의 조립공정에 적용된다. 예로서 자동차 내연엔진의 연료분사장치의 성능을 결정짓는 핵심부품은 연료 분사량과 형태에 직접적인 영향을 미치는 바디와 니들이다. 즉, 바디의 내경과 니들의 외경으로 정해지는 두 부품의 간격(clearance)이 아주 정밀하지 않으면 연료의 분사가 균일하지 않게 되어 엔진이 기대되는 성능을 발휘할 수 없게 된다. 그러나 제품의 품질특성인 조립된 두 부품 사이의 간격을 정밀하게 구현하기 위해 각 부품을 극히 정밀하게 가공할 경우 초정밀 가공에 따른 원가의 급격한 상승으로 인한 부담을 피할 수가 없게 된다. 이 때 비록 각 부품의 가공정밀도는 불충분하더라도 조립제품의 품질특성인 간격이 목표치에 최대한 가깝게 되도록 해주는 바디와 니들을 선택하여 조립함으로써 부품 가공원가 상승의 부담을 줄이면서 조립제품의 품질특성에 요구되는 규격을 만족시킬 수 있다. 이와 같은 선택조립방식은 상대적으로 덜 정밀한 부품가공공정으로 훨씬 정밀도가 높은 제품을 생산할 수 있다는 있다는 이점이 있으나 조립 대상부품을 고르는 과정에서 미조립 상태로 남게 되는 잉여부품 문제가 수반된다. 잉여부품도 원가상승의 요인이므로 잉여부품의 발생량은 최소화하면서 제품정밀도를 요구수준 이상으로 높이는 것이 선택조립의 목표가 된다고 하겠다. 본 절에서는 이와 같은 목표 달성을 위해 과거에 연구된 여러 가지 선택조립방식들을 적절하게 분류하여 살펴본다.
과거에 연구된 선택조립 방식들은 크게 치수분할방식(dimensional partitioning criterion; DP)과 통계적 매칭 방식(statistical matching criterion)의 두 가지 유형으로 구분할 수 있다. 치수분할방식은 생산된 두 종류의 부품 치수에 의해 각기 여러 범주로 분류한 후 대응되는 범주에 속한 부품들끼리 짝을 맞추어 조립하는 방식이다. 치수분할방식의 대표적인 것으로 등간격분할방식(erqual width partitioning)과 등면적분할방식(equal area partitioning)이 있다. 전자는 치수를 측정하여 범주로 분류할 때 각 범주의 치수 폭이 동일하도록 하는 방식이고 후자는 각 범주에 속할 기대 부품수를 동일하도록 하는 방식이다.
한편, 통계적 매칭 방식은 일련의 생산된 두 종류의 부품들을 사전에 정해진 범주로 분류해 넣지 않고 통계적 방법으로 짝을 맞추어 조립하는 방식이다. 별도로 부품을 선택하는 절차가 없는 임의조립방식도 통계적 매칭 방식이라 할 수 있으나 선택조립방식이라 볼 수는 없다. 기존에 연구된 통계적 매칭 방식으로 최선 매칭(best matching; BM)이 있다. 본 연구에서는 기존에 따로 연구된 논문은 없으나 직관적으로 조립정밀도 향상의 효과를 예측할 수 있는 순서 매칭(ordered matching; OM)을 제시하고 함께 포함하여 분석 결과를 비교한다. 따라서 본 논문에서 고려되는 선택조립방식은 Figure 1과 같이 요약할 수 있다.
Figure 1.
Type of selective assembly 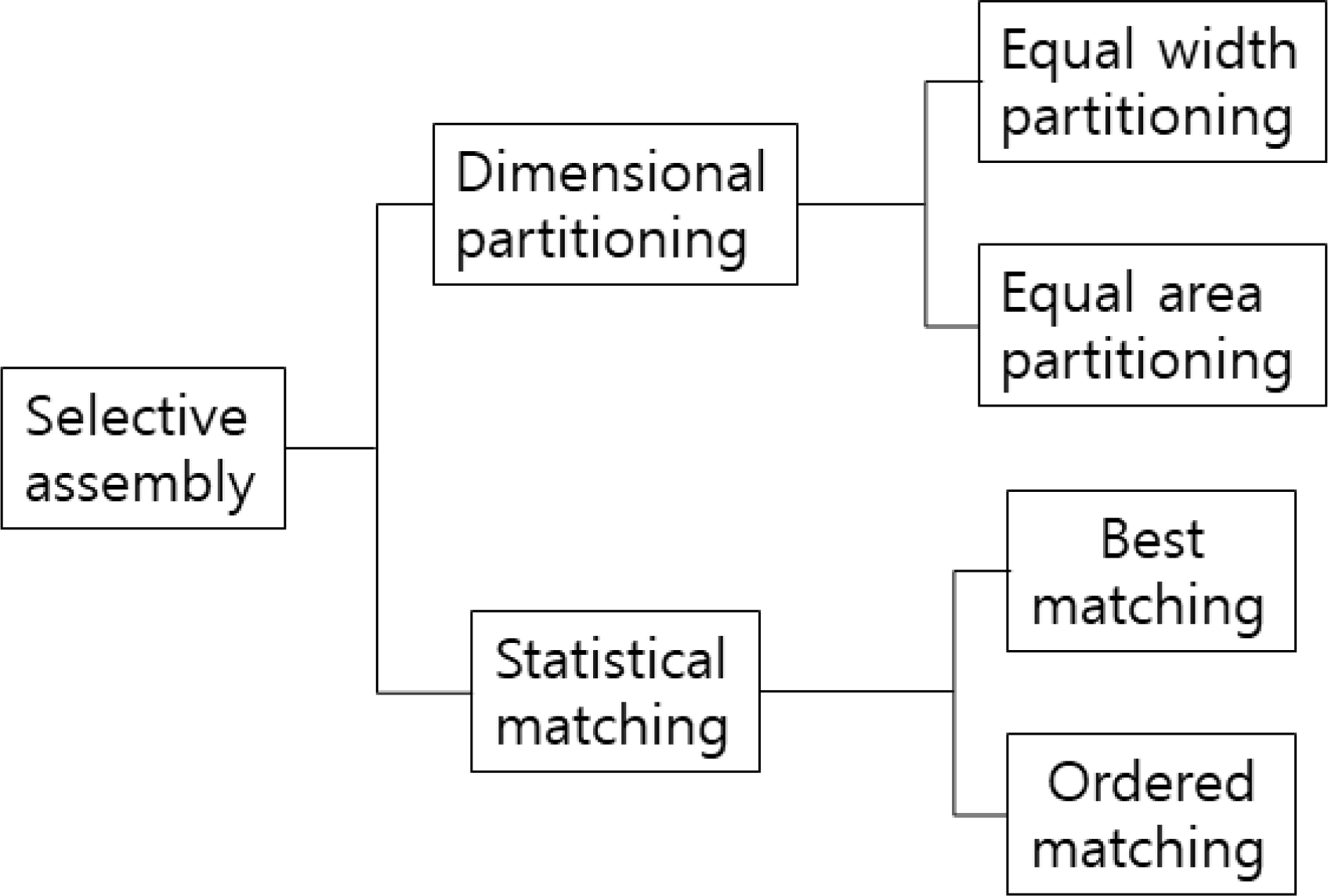
2.2 치수분할방식
치수분할방식은 생산된 부품의 치수를 측정하여 소속 범주로 분류한 후 대응되는 범주에 속한 부품들끼리 짝을 맞추어 조립하는 방식이다. 이 때 기준이 되는 범주의 수와 각 범주의 경계치를 부품별로 사전에 정해 두어야 하며 다음 절차에 따라 실시한다.
① 먼저 조립품에 설정된 허용공차나 규격과 경제적인 면을 고려하여 범주의 수 n과 경계치를 설정해 둔다.
② 조립품을 구성하는 두 핵심부품(부품 A와 B)의 생산라인에서 각 부품들을 독자적으로 생산한다.
③ 각 부품이 생산되는 즉시 치수를 측정하여 해당 범주의 부품 함(bin)에 넣는다.
④ n개의 쌍으로 준비된 부품 A와 B의 부품 함에서 A 부품과 B 부품이 모두 들어 있는 쌍이 있는지 확인한다.
⑤ A 부품과 B 부품이 모두 들어 있는 쌍의 부품 함이 없으면 다음 부품의 생산을 기다린다.
⑥ A 부품과 B 부품이 모두 들어 있는 쌍의 부품 함에서 각각 랜덤하게 한 부품씩 선택하여 조립한다.
Figure 2.
Selective assembly procedure of two components 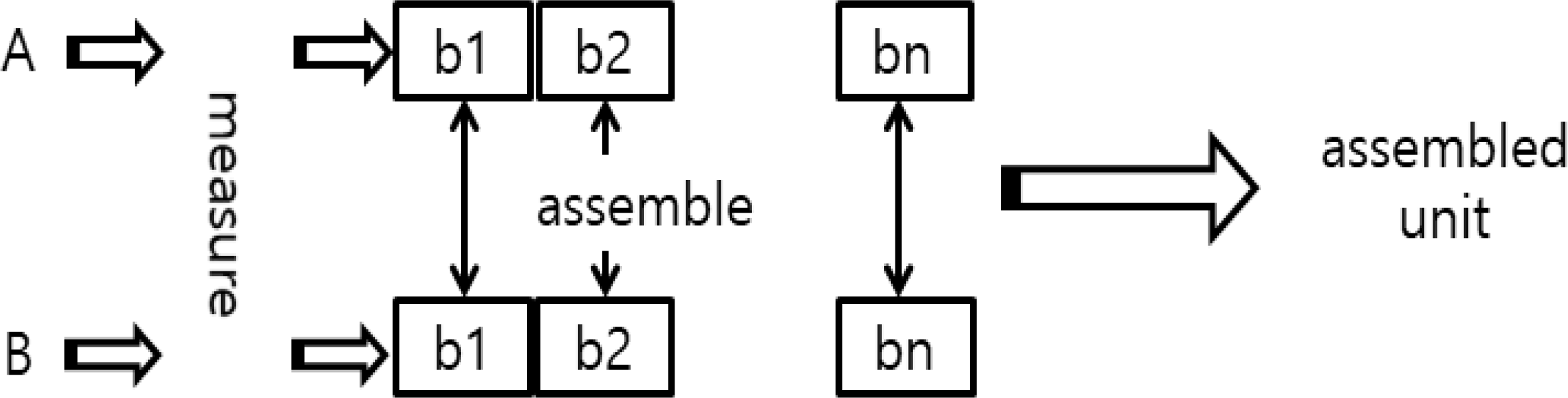
이와 같은 치수분할방식에는 부품 함에 분류해 넣는 치수의 경계치를 어떻게 설정하는가에 따라 등간격분할방식과 등면적분할방식으로 구분할 수 있다. 등간격분할방식은 Figure 3에서 보는 바와 같이 부품 A와 B를 치수 기준으로 분류되는 범주의 폭이 동일하도록 분할하는 방식이다. 이 방식은 조립품의 정밀도는 보증할 수 있으나 대응하는 범주에 속한 부품 A와 B의 수가 일치하지 않는 문제가 있다. 그래서 장기적으로 조립되지 못하고 폐기되어야 하는 부품이 증가하게 되어 생산원가의 상승원인이 된다.
Figure 3.
Equal width partitioning for components A and B 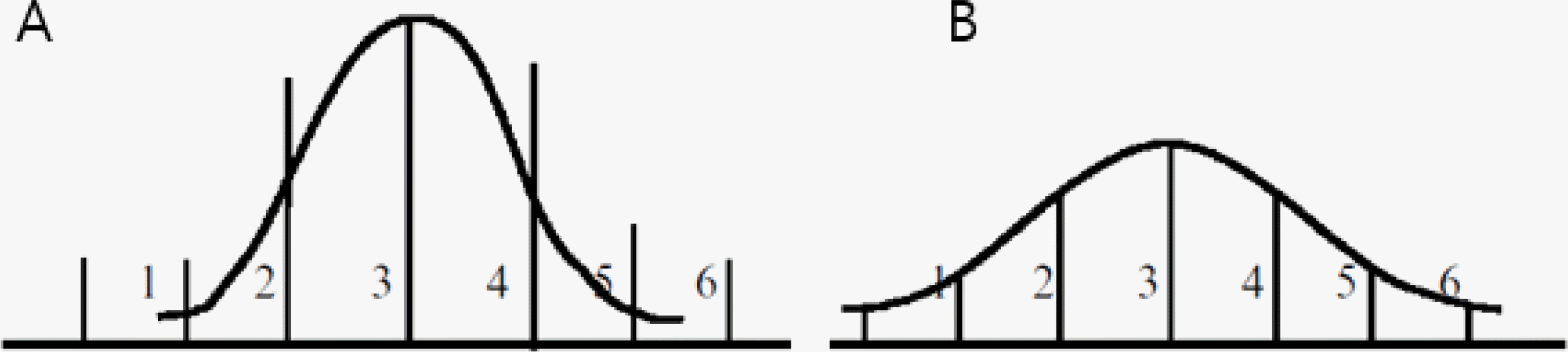
다음으로 등면적분할방식은 등확률분할방식으로 이해할 수 있는데 두 부품이 각 범주에 속할 확률이 동일하도록 분할하는 방식이다. Figure 4에서 확률밀도함수를 각 구간별로 적분하면 확률밀도함수로 결정되는 해당 구간의 면적이 된다. 이것은 부품의 치수를 나타내는 확률변수가 그 구간에 속할 확률과 같다. 이와 같은 등면적분할방식에 의해 선택조립을 실시할 경우 각 범주에 속할 기대 부품수가 같게 되므로 장기적으로는 잉여부품이 발생하지 않게 된다. 그러나 이 경우 등간격분할방식과는 달리 조립제품의 정밀도가 목표수준에 이르지 못할 수도 있으며 경우에 따라 불량 발생도 피할 수 없다.
Figure 4.
Equal area partitioning for components A and B 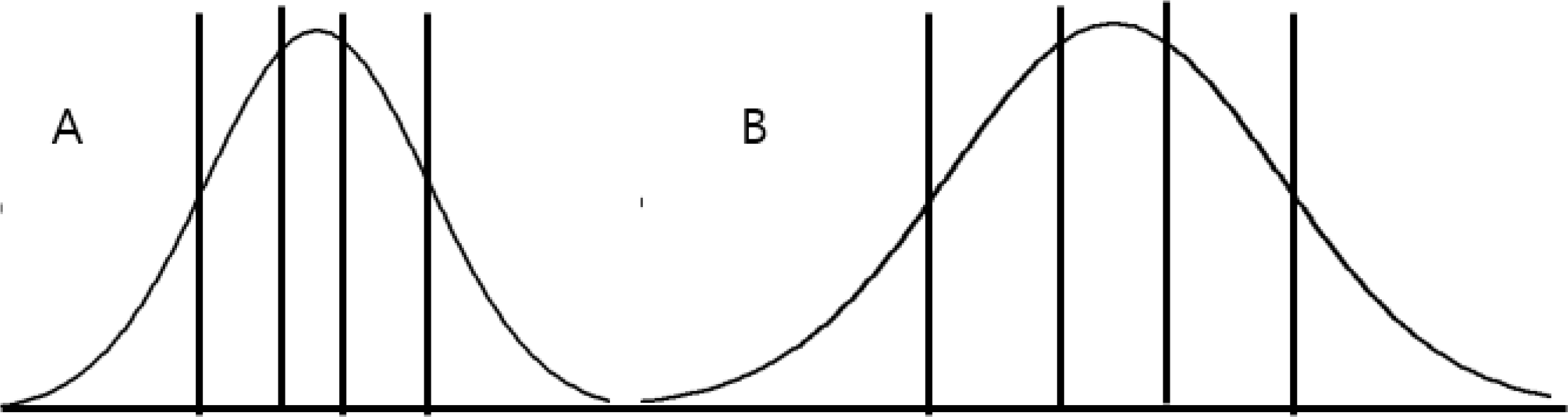
2.3 통계적 매칭 방식
통계적 매칭 방식은 따로 범주를 구분하지 않은 채 생산된 일정 개수(n)의 부품 A와 B를 어떤 방식으로 매칭시켜 조립할 것인가에 관련된다. 여기서는 상식적인 선에서 쉽게 이해되는 최선 매칭 방식과 순서 매칭 방식을 고려한다. 먼저 최선 매칭 방식은 Figure 5에서 보는 바와 같이 부품 A와 B에 대해 n2개의 가능한 매칭을 모두 검토하여 조립품의 치수가 목표 치수에 가장 가깝게 되는 조합을 선택하여 조립하는 방식이다. 이 방식은 현장에 적용할 때 많은 계산과 비교가 요구된다는 단점이 있어 생산속도를 저하시킬 우려가 있다. 그러나 처음 계산이 이루어지고 나면 최선의 조합이 조립되어 빠져 나간 후 n-1개의 남은 A 부품과 B부품의 측정치와 비교 정보들이 남아 있을 것이다. 따라서 새로이 생산된 한 쌍의 부품을 보태어 최선 매칭을 찾는 것은 적절한 알고리즘만 개발되면 시간을 현저하게 단축할 수 있고 컴퓨터의 성능 향상에 따라 최선 매칭 탐색 시간이 크게 문제되지 않을 수도 있다.
Figure 5.
Best matching criterion for components A and B 
다음으로 순서 매칭 방식은 Figure 6에서 보는 바와 같이 생산된 n개의 A부품과 B부품을 치수크기 순으로 배열한 다음 각 순서에 대응되는 부품을 선택하여 조립하는 방식이다. 이 방식은 최선 매칭 방식보다는 조립품의 치수 정밀도가 떨어지겠지만 계산 및 비교 시간은 더 짧게 걸린다.
Figure 6.
Ordered matching criterion for components A and B 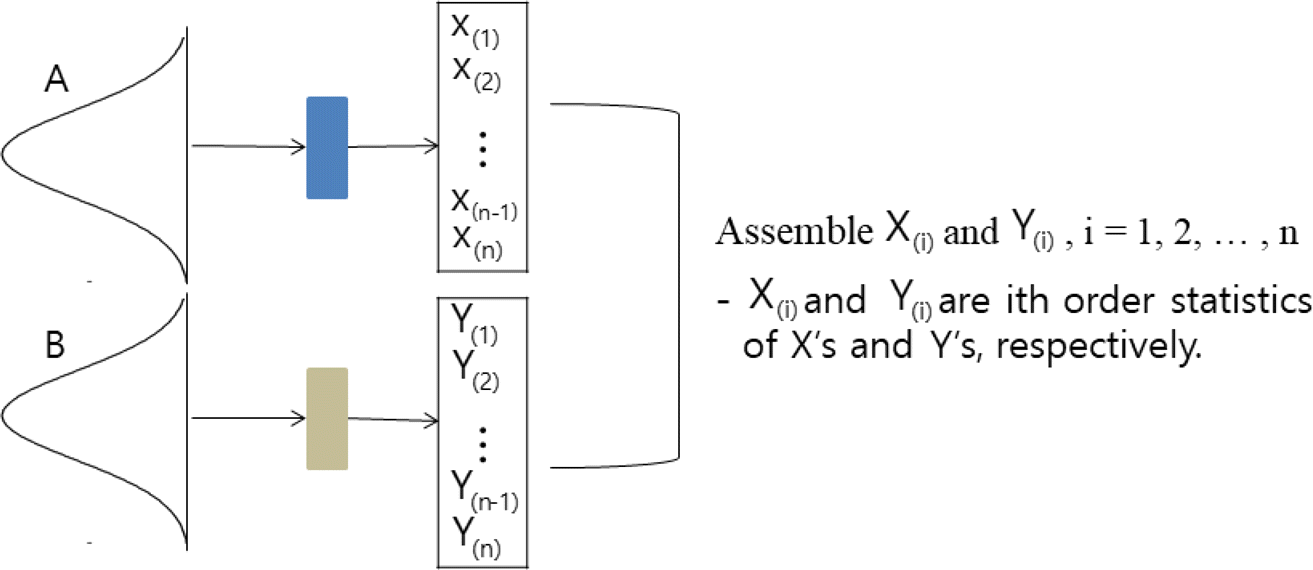
3. 선택조립 시뮬레이션
3.1 시뮬레이션 방법
시뮬레이션을 실시하기 위해 A의 치수와 B의 치수는 서로 독립이고 표준편차가 같은 정규분포를 따른다고 가정하였다. 기본적으로 부품 A와 B는 별개의 라인에서 생산되므로 독립성을 가정하였고 가공치수는 둘 다 망목특성으로 대칭분포를 할 것이므로 정규성을 가정하였다. 또한, 같은 회사에서 가공기술의 수준이 라인마다 큰 편차가 있지 않을 것이므로 등분산 가정을 채택하였다. 따라서 여기서는 표준편차가 같은 경우에 대해서만 시뮬레이션하고 표준편차가 다름으로 인한 영향은 다음 절에서 살펴보기로 한다.
표준편차가 같을 경우 선택조립의 결과에 영향을 미치지 않고 두 부품의 치수를 적절하게 변환하여 표준정규분포를 따르게 할 수 있다. 또한, 조립품의 품질특성치 (Bx치수 Ax치수)도 적절하게 변환하여 조립품 허용공차가 ±δ로 주어진 것으로 단순화할 수 있다. 또 두 부품 치수의 표준편차가 같고 정규분포를 따른다면 등 간격분할방식과 등 면적분할방식은 똑같게 될 것이므로 이들을 묶어 치수분할방식으로 취급하였다. 다만 최선 매칭 방식과 순서 매칭 방식은 부품 치수의 표준편차가 같더라도 조립품 치수의 정밀도에는 차이가 있을 것이므로 따로 취급하였다. 따라서 여기서 시뮬레이션을 실시하여 비교하는 선택조립방식은 치수분할방식, 최선 매칭 방식 및 순서 매칭 방식의 세 가지가 될 것이다.
시뮬레이션은 JAVA 컴퓨터 프로그램으로 하였고 부품별로 10,000 단위를 생산하는 것으로 하였다. 그 이상 생산하는 경우도 시뮬레이션 하였으나 큰 차이가 없었다. 구체적인 시뮬레이션 절차는 다음과 같다.
(i) 두 부품 A, B의 치수에 대해 각각 표준정규분포를 따르는 난수를 10,000개씩 생성한다. -
(ii) n=2,5,10,20에 대해 생성된 순서대로 A와 B에 대해 다음과 같이 선택조립을 실시한다.
-
치수분할방식일 경우
① Figure 2와 같이 생산된 순서에 따라 처음 얻어진 A와 B 치수에 근거하여 각각 n개의 부품 함 중 어느 하나에 분류해 넣는다. ② 쌍으로 대응되는 A와 B의 함에 모두 부품이 있는지 확인하고 있으면 이들을 조립한다. 조립된 부품 A와 B의 치수 차이는 제품 특성치 데이터로 저장한다. ③ 그렇지 않으면 이들은 그냥 두고 다음에 얻어진 A와 B를 치수에 근거하여 각각 n개의 부품 함 중 어느 하나에 분류해 넣는다. ④ ②와 ③의 절차를 생성된 10,000개에 대해 순차적으로 반복 적용한다.
-
최선 매칭 방식일 경우
① Figure 5와 같이 생산된 순서에 따라 처음 얻어진 개의 A 부품과 B 부품의 모든 조합에 대해 치수 차이를 계산한다. ② 계산된 n2 개의 치수 차이의 값들 중 가장 0에 가깝게 되는 A와 B부품을 조립한다. 조립된 부품 A와 B의 치수 차이는 제품 특성치 데이터로 저장한다. ③ 조립된 부품을 제외하고 다음 부품 A와 B를 추가하여 n개의 쌍을 얻는다. ④ 다시 n개의 A 부품과 B 부품의 모든 조합에 대해 치수 차이를 계산한다. ⑤ ②, ③ 및 ④의 절차를 생성된 10,000개에 대해 순차적으로 반복 적용한다.
-
순서 매칭 방식일 경우
① Figure 6와 같이 생산된 순서에 따라 처음 얻어진 n개의 A 부품과 B 부품을 각각 치수 크기에 따라 순서대로 정렬한다. ② 같은 순위의 부품 A와 B를 조립한다. 연료분사장치 예의 경우 n개 중 내경이 가장 큰 바디는 외경이 가장 큰 니들과 조립함으로써 조립 후 두 부품의 간격이 목표 치수에 가깝도록 하는 것이다. 조립된 n쌍의 부품 A와 B의 치수 차이는 제품 특성치 데이터로 저장한다. ③ 다음 n개의 A 부품과 B 부품을 대상으로 각각 치수 크기에 따라 순서대로 정렬한다. ④ ②와 ③의 절차를 생성된 10,000개에 대해 순차적으로 반복 적용한다.
(iii) 선택조립 결과 얻어진 제품치수 데이터를 사용하여 허용공차 δ=0.5,1.0,1.5일 경우에 대해 각 선택조립방식별로 불량률 및 미조립 부품수를 계산하여 비교한다.
허용공차별 불량률의 계산 근거는 다음 절에서 살펴보겠지만, 여기서 조립품 허용공차 δ=0.5 는 불량률이 약 70%에 이르는 공정으로 가공정밀도가 극히 저조한 수준을 나타낸다. 즉, 현재 공정의 가공기술수준으로 제품에 요구되는 높은 정밀도를 충족하기 어려운 상태를 의미한다. δ=1.5 는 δ= 0.5 보다는 정밀도가 높지만 불량률이 약 30%에 달해서 제품의 규격을 만족시키기에는 부족한 공정능력 수준으로서 공정능력의 차이에 따른 선택조립의 효과를 살펴보기 위해 다른 값의 허용공차를 적용해 본 것이다. 다만, 선택조립은 원래 부족한 부품가공기술 수준으로 높은 정밀도의 제품을 생산하기 위해 도입된 공법이므로 δ가 더 큰 경우, 즉, 부품가공공정의 능력이 더 큰 경우는 고려하지 않았다.
또한, n 값과 관련 여러 가지 값에 대해 시뮬레이션을 실시하여 분석하여 검토하여 의미 있는 차이를 보이는 것으로 n=2,5,10,20 을 대표로 선택하였다. 즉, n=3,6,12,30 등 다른 값으로 선택하여도 분석 결과의 경향이나 흐름을 비교하는데 별다른 차이는 없다.
3.2 선택조립방식별 시뮬레이션 결과
먼저 치수분할방식부터 살펴보면 Table 1에서 보는 바와 같이 공정의 가공 정밀도가 매우 부족한 경우에도 범주의 수를 증가시킴에 따라 불량률이 빠른 속도로 감소함을 알 수 있다. 반면에 조립되지 못하고 남는 잉여부품의 수는 증가하지만 n=2,5,10,20 에 따른 잉여부품의 수는 m=152,158,206,432 정도로서 기하급수로 증가하지는 않는다.
Table 1.
% fraction defectives of dimensional partitioning for n = 2, 5, 10, 20
|
n
|
δ = 0.5 |
δ = 1.0 |
δ = 1.5 |
|
2 |
52.12 |
23.06 |
8.15 |
|
5 |
38.86 |
8.45 |
0.00 |
|
10 |
5.33 |
0.00 |
0.00 |
|
20 |
0.01 |
0.00 |
0.00 |
Figure 7.
% fraction defectives of dimensional partitioning for n=2,5,10,20 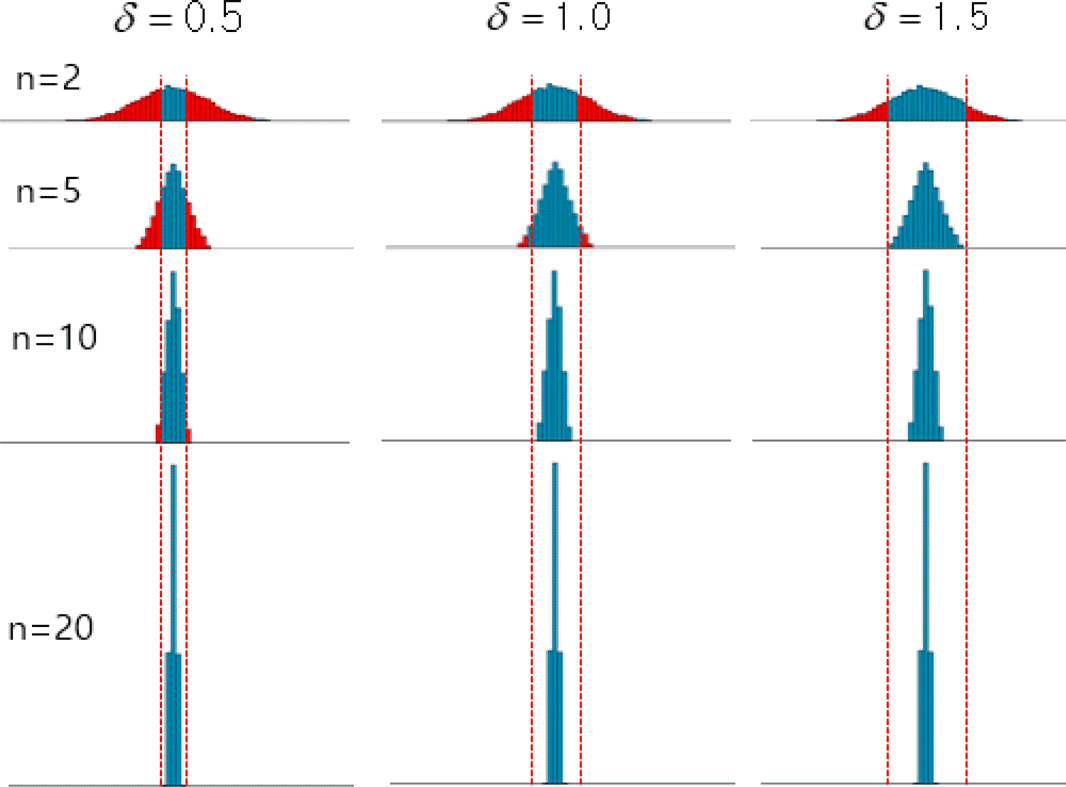
다음으로 최선 매칭 방식을 표로 정리하면 Table 2와 같은데 역시 n의 증가에 따라 불량률이 급격하게 감소함을 알 수 있다. 범주의 수 n이 크지 않을 경우 치수분할방식에 비해 최선 매칭 방식이 더 낫고 n이 증가함에 따라 치수분할방식이 낫게 되지만 잉여부품문제가 증가하게 된다. 최선 매칭 방식은 생산 활동이 진행 중인 경우에는 항상 2n 개의 부품이 재공품으로 있게 된다는 문제가 있다. 마찬가지로 그림으로 변화를 살펴보면 Figure 8과 같다.
Table 2.
% fraction defectives of best match for n = 2, 5, 10, 20
|
n
|
δ = 0.5 |
δ = 1.0 |
δ = 1.5 |
|
2 |
47.97 |
19.63 |
6.75 |
|
5 |
17.84 |
3.46 |
0.73 |
|
10 |
6.34 |
1.03 |
0.15 |
|
20 |
3.44 |
0.48 |
0.05 |
마지막으로 순서 매칭 방식을 표로 정리하면 Table 3과 같은데 역시 n 의 증가에 따라 불량률이 감소하긴 하지만 그 정도가 완만함을 알 수 있다. Figure 8과 Figure 9를 비교해보면 알 수 있듯이 순서 매칭 방식은 최선 매칭 방식에 비해 조립제품의 정밀도 개선이라는 측면에서 효과적이지 못하다. 다만, 이 방식은 잉여부품이나 재공품의 재고를 유지하지 않아도 된다는 장점은 있다.
Figure 8.
% fraction defectives of best match for n=2,5,10,20 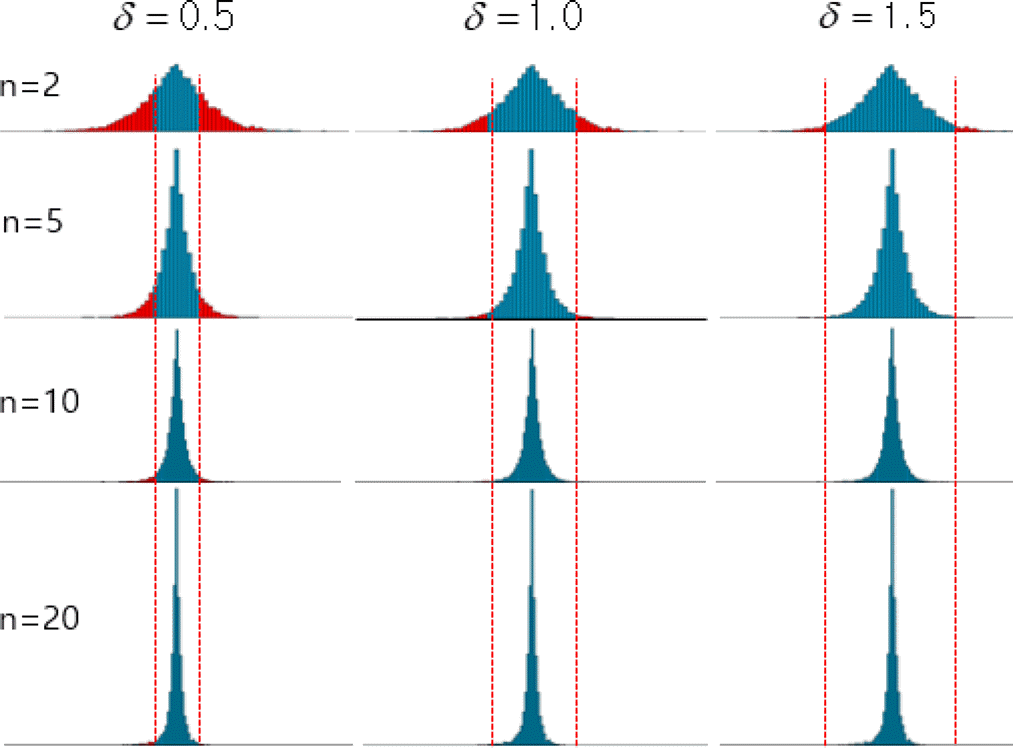
Figure 9.
% fraction defectives of ordered match for n=2,5,10,20 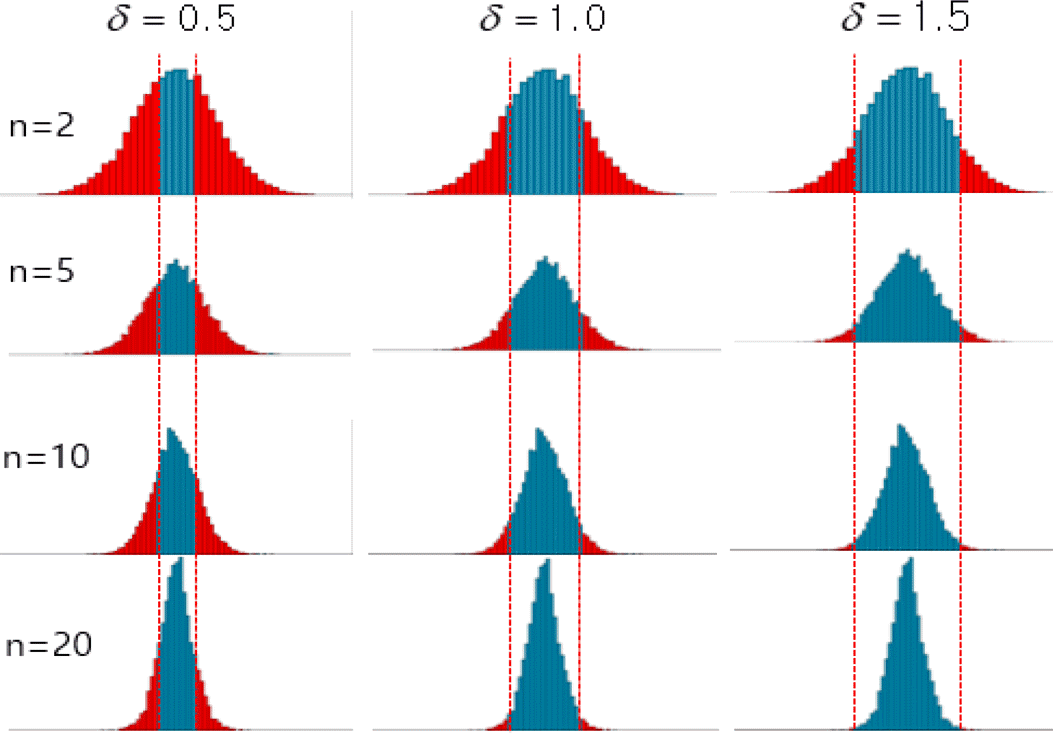
Table 3.
% fraction defectives of ordered match for n = 2, 5, 10, 20
|
n
|
δ = 0.5 |
δ = 1.0 |
δ = 1.5 |
|
2 |
66.99 |
38.73 |
19.30 |
|
5 |
54.73 |
23.66 |
7.68 |
|
10 |
42.48 |
11.92 |
2.28 |
|
20 |
28.65 |
4.41 |
0.52 |
3.3 선택조립방식의 비교
선택조립의 기본적인 목표는 가공능력이 떨어지는 부품 생산라인을 이용하여 큰 비용의 증가 없이 높은 정밀도의 조립제품을 얻고자 하는데 있다. 따라서 여기서는 3.2절의 시뮬레이션 결과를 토대로 이러한 목적에 비추어 효용성이 떨어지는 순서 매칭(OM) 방식은 제외하고 치수분할(DP)방식과 최선 매칭(BM) 방식에 대해서만 비교해보기로 한다.먼저 부품가공공정의 정밀도가 아주 떨어지는 δ=0.5 인 경우를 살펴보자. A 부품의 치수 X와 B 부품의 치수 Y의 분포가 표준정규분포를 따른다고 한다면 두 부품 치수 차이 (X-Y)의 분포는 평균이 0, 분산은 2인 정규분포를 따르게 될 것이다. 따라서, 만약 이 경우에 선택조립을 하지 않고 공정을 진행한다면 조립제품의 불량률은 규격한계인 ±δ±0.5 를 벗어나게 될 확률로서
로서 72.4%에 이를 것이다. 이와 같이 공정능력이 극히 저조할 경우에도 n=10 인 선택조립을 실시하면 Figure 10 (a)에서 보는 바와 같이 불량률을 5% 수준으로 낮출 수 있다. 이때 n 의 증가에 따라 처음에는 최선 매칭 방식이 치수분할방식보다 더 급격한 개선효과를 가진다는 것을 알 수 있다. 그러나 n=10 정도 이상이 되면 치수분할방식의 개선효과가 더 크게 나타난다.
Figure 10.
Comparison of best matching and dimensional partitioning 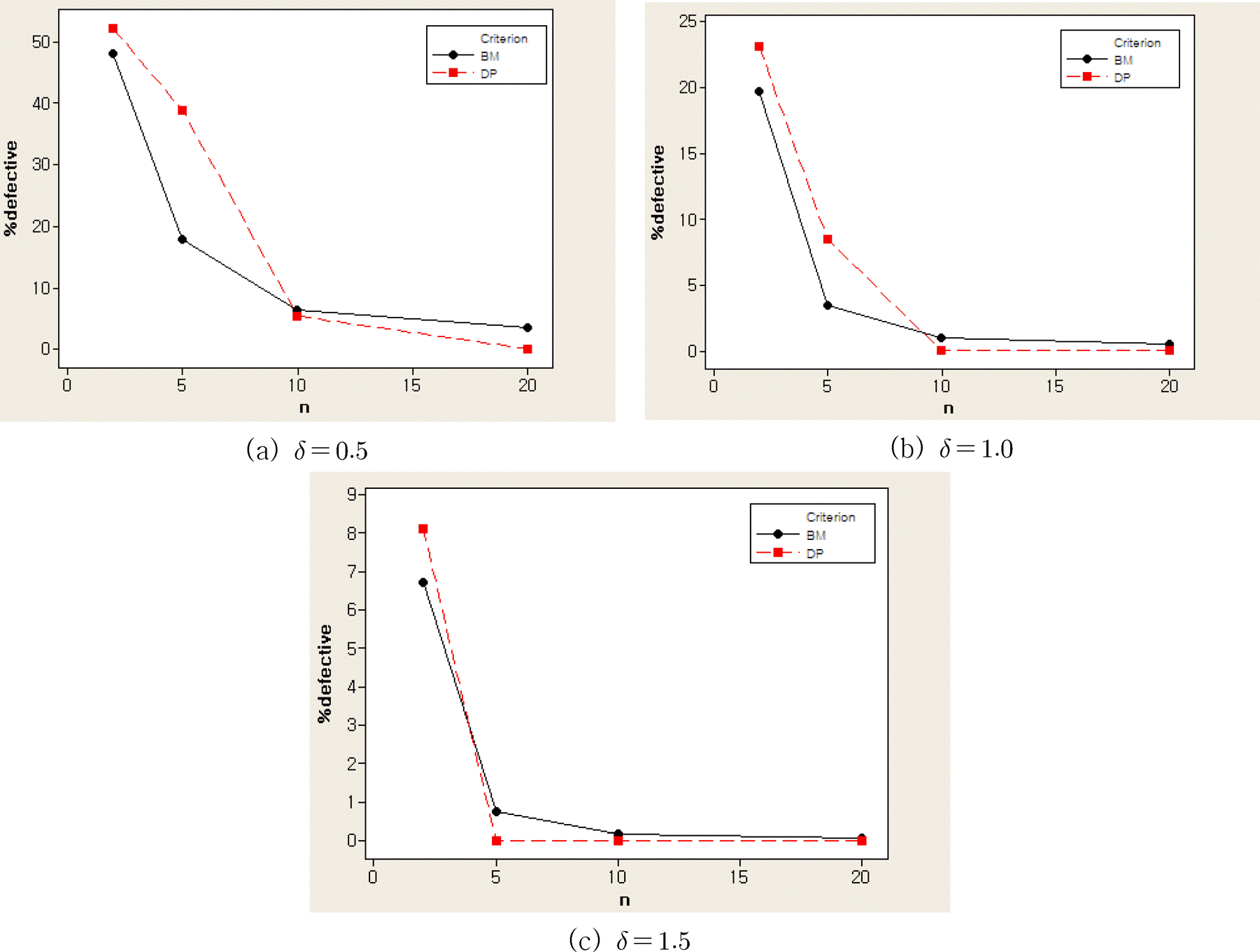
다음으로 δ=1.0 인 경우 선택조립을 하지 않고 공정을 진행한다면 제품 불량률은
로서 48.0%에 이를 것이다. 이 때, n=10 인 선택조립을 실시하면 Figure 10 (b)에서 보는 바와 같이 불량률을 1% 수준으로 낮출 수 있다. δ=0.5 인 경우와 마찬가지로 n 의 증가에 따라 처음에는 최선 매칭 방식이 치수분할방식보다 더 급격한 개선효과를 가진다는 것을 알 수 있다. 그러나 n=10 정도 이상이 되면 차이가 크지는 않지만 치수분할방식의 개선효과가 더 크게 나타난다. 다음으로 δ=1.5 인 경우 선택조립을 하지 않고 공정을 진행한다면 제품 불량률은
로서 28.9%에 이를 것이다. 이 때에는 n=5 정도만 하여도 선택조립을 실시하면 Figure 10 (c)에서 보는 바와 같이 불량률을 1% 미만으로 낮출 수 있다. 이 경우에는 n 의 증가에 따라 처음에 치수분할방식이 최선 매칭 방식보다 더 급격하게 불량률이 감소한다. n=10 정도 이상이 되면 불량이 거의 발생하지 않는다. 종합하여 정리해보면 최선 매칭 방식은 치수분할방식과 거의 대등한 개선효과를 가지면서도 잉여부품 문제를 갖지 않는 유망한 방식임을 알 수 있다. 특히 범주의 수 n이 그리 크지 않을 때는 최선 매칭 방식이 치수분할방식보다 더 효과적이다. 그런데 n이 크면 불량률은 두 방식 모두 극히 작게 되는데 비해 치수분할방식의 잉여부품문제가 커지게 되므로 현실적으로 최선 매칭 방식이 가장 추천할 만한 방식이라 할 수 있다. 또한 Figure 9 (c)의 최선 매칭 방식의 불량률 변화에서 보는 바와 같이 불량률이 29% 정도의 공정일 경우에도 n=10 정도면 선택조립의 불량률이 치수분할방식과 거의 대등한 수준이 된다. 요즈음의 컴퓨터 성능을 고려하면 n=10 정도일 경우 최선의 부품조합을 찾기 위한 계산 시간도 전혀 문제가 안 될 것이다. 이것은 기존에 많이 사용되어 왔던 치수분할방식보다는 최선 매칭 방식을 기반으로 하여 선택조립공정을 설계하는 것이 낫다는 것을 의미한다.
4. 가공정밀도의 영향분석
4.1 잉여부품 문제
측정오차가 없다는 전제 하에서 두 부품의 표준편차가 같기만 하다면 부품의 가공정밀도가 많이 부족하더라도 선택조립에 의해 제품의 정밀도(조립정밀도)를 크게 향상시킬 수 있다. 그런데 두 부품의 표준편차에 차이가 크면 선택조립에 의한 개선효과를 기대할 수 없게 된다. 즉, 선택조립을 실시하기 위해 가장 중요한 기본 전제조건으로 측정오차가 없을 것과 각 부품의 가공정밀도가 동일하거나 비슷해야 한다는 것이다. 산업현장에서는 조립 제품을 구성하는 쌍을 이루는 두 핵심 부품은 같은 공장에서 공정만 달리하여 가공되는 것이 일반적이다. 같은 공장에서 같은 인력이 작업하는 상황이기 때문에 두 부품에 대한 가공기술의 수준도 거의 같을 것이므로 전 절에서는 두 부품치수의 표준편차가 같다고 가정하였다. 그러나 두 부품 치수의 표준편차가 완전하게 일치하기는 어려울 것이므로 여기서는 어느 정도의 차이가 있을 경우 선택조립에 어떤 영향을 주게 되는지 살펴본다.
먼저 선택조립에 치수분할방식 중 등간격분할방식을 적용할 경우, 폐기해야 할 잉여부품의 양이 많아지게 된다. 예로서 A부품의 표준편차가 σ이고 B부품의 표준편차는 1.5σ 라 하고 평균은 0이라고 하자. 또 ±3σ 를 벗어나는 부품은 모두 버리고 범주의 간격을 1.0σ 로 하여 등간격분할방식으로 선택조립을 실시한다고 하자. A부품의 폐기비율은 0.27%이고 B부품 중 ±3σ 를 벗어나는 비율은
이므로 4.55%의 부품은 폐기처분하게 될 것이다. 또 A부품과 B부품의 대응 범주별 소속 확률을 비교하여 잉여부품의 비율을 계산하면 Table 4에서 보는바와 같이 A부품의 경우 잉여부품이 18.76%, B부품의 경우 잉여부품이 14.5%에 이르게 된다. 총 부품 중 조립되지 못하고 폐기되는 비율이 거의 20%에 육박하게 되므로 심각한 손실을 초래하게 된다.
Table 4.
Percentage of mismatched components
|
범주 |
A부품 비율 |
B부품 비율 |
잉여부품 비율 |
잉여부품 |
|
1 |
2.14 |
6.85 |
4.71 |
B |
|
2 |
13.39 |
16.13 |
2.54 |
B |
|
3 |
34.13 |
24.75 |
9.38 |
A |
|
4 |
34.13 |
24.75 |
9.38 |
A |
|
5 |
13.59 |
16.13 |
2.54 |
B |
|
6 |
2.14 |
6.85 |
4.71 |
B |
따라서 이와 같은 잉여부품문제를 해결하기 위해 고안된 방식이 등면적분할방식이다. 이 방식은 A부품과 B부품을 선택하여 조립할 때 상호 대응되는 범주에 속한 부품비율이 동일하게 되도록 범주를 설정하는 방식이다. 예로서 A부품의 표준편차가 σ이고 B부품의 표준편차는 1.5σ 라 한다면 A부품의 첫 번째 범주는 [-3σ,-2σ] 로 설정하고 B부품의 첫 번째 범주는 [-4.5σ,-3σ] 로 설정한다. 이렇게 하면 A부품과 B부품이 각 대응범주에 속할 확률이 동일하게 되므로 장기적으로는 잉여부품 문제가 발생하지 않는다.
한편, 통계적 매칭 방식은 기본적으로 잉여부품이 발생하지 않는 방식이다. 따라서 최선 매칭 방식이나 순서 매칭 방식을 적용할 때는 각 부품의 가공 정밀도가 다르다고 하더라도 잉여부품 문제를 따로 고려할 필요가 없다.
4.2 조립정밀도
여기서는 가공정밀도 차에 따른 치수분할방식과 통계적 매칭 방식의 조립정밀도를 비교해본다. 치수분할방식으로는 잉여부품문제가 발생하지 않는 등면적분할방식을 고려하고 통계적 매칭 방식으로는 이전의 분석에서 보다 나은 결과를 보여준 최선 매칭 방식을 고려하기로 한다. 또, 가공정밀도의 차이는 B부품치수의 표준편차가 A부품치수의 표준편차의 1.25배일 경우와 1.5배일 경우를 고려한다. 그리고 나머지 시뮬레이션의 조건은 3절과 동일하게 하였다.
부품의 가공정밀도에 차이가 있어서 치수의 표준편차가 상이할 경우에도 선택조립을 적용하면 Figure 11에서 보는 바와 같이 조립정밀도가 향상되기는 하지만 그 정도가 다소 둔화된다. 최선 매칭 방식의 경우에는 향상의 정도 면에서는 부품치수의 표준편차가 조금 다르더라도 거의 비슷하고 등면적분할방식은 다소 둔화된 개선을 보여준다. 예를 들어 Table 5에서 δ= 0.5 일 경우 n=2 및 n=5 인 선택조립의 조립불량률을 비교해보면 최선 매칭 방식은 σ ν=1.00,1.25 및 1-50 에 대해 거의 균일하게 30%정도의 개선을 유지하지만 등면적분할방식은 13.26%, 11.7%, 및 10.66%로 조금씩 둔화되는 경향을 보여준다.
Figure 11.
Fraction defective for selective assembly when σY = 1.25 and σY=1.50 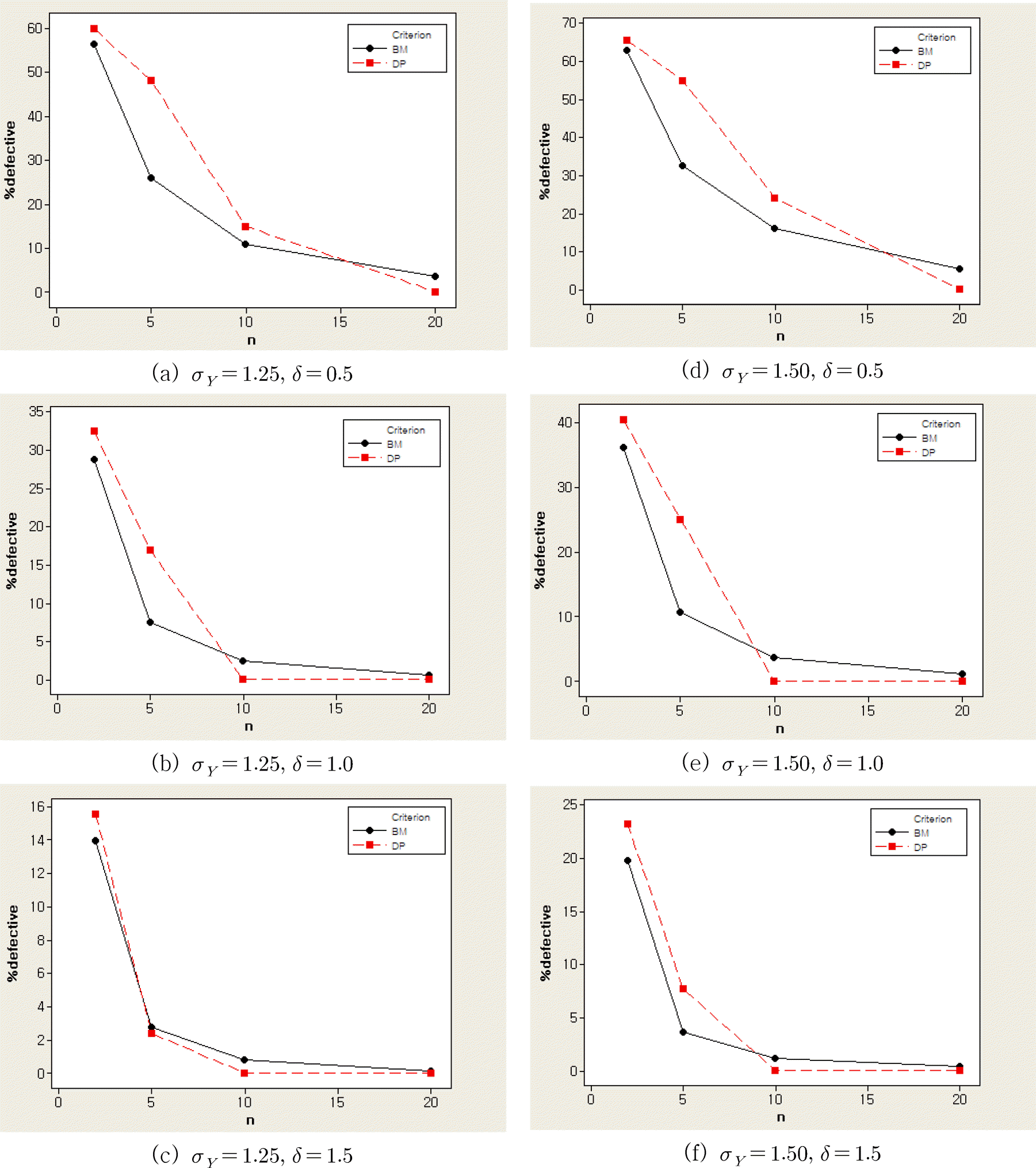
Table 5.
Reduction in fraction defective when σY = 1.00, 1.25 and 1.50
|
σY = 1.00 |
σY = 1.25 |
σY = 1.50 |
|
|
DP |
BM |
DP |
BM |
DP |
BM |
|
n = 2
|
52.12 |
47.97 |
59.86 |
56.32 |
65.50 |
62.72 |
|
n = 5 |
38.86 |
17.84 |
48.09 |
25.92 |
54.84 |
32.52 |
|
difference |
13.26 |
30.13 |
11.77 |
30.40 |
10.66 |
30.20 |
따라서 두 부품의 가공정밀도에 차이가 다소 나더라도 최선 매칭 방식에 의한 선택조립을 하게 되면 비교적 균일한 정도의 개선효과를 기대할 수 있게 된다. 또한 선택조립을 위한 범주의 수가 작을 때에는 Figure 11에서 보는 바와 같이 최선 매칭 방식이 더 급속한 개선을 보여주고 있다.
5. 결 론
선택조립을 위한 방법으로 치수분할방식과 통계적 매칭 방식의 효용성에 대해 시뮬레이션을 이용하여 분석하였다. 치수분할방식으로서는 등간격분할방식이 산업현장에서 널리 사용되고 있으나 표준편차가 다른 경우 조립되지 못하고 남는 잉여부품 문제가 발생하여 이를 보완할 방법으로 등면적분할방식을 생각할 수 있다. 그러나 비록 다른 부품이라 하더라도 같은 공장 내에서 가공될 경우 가공정밀도가 거의 같을 것이므로 표준편차가 같을 경우에 대해서 먼저 시뮬레이션하고, 부품 가공정밀도가 다른 경우로 확장하여 분석하였다.
총 10,000개의 제품을 생산하는 것으로 하여 시뮬레이션하여 치수분할방식, 최선 매칭 방식 및 순서 매칭 방식을 비교한 결과 조립품 정밀도 향상이라는 측면에서는 치수분할방식과 최선 매칭 방식이 거의 대등한 효과가 있음을 보여주었고 순서 매칭 방식은 이 두 방식에 비해 정밀도 향상 효과가 상당히 작았다. 선택조립에서 사용할 범주의 수가 작으면 최선 매칭 방식이 치수분할 방식보다 선택조립의 개선 효과가 대체로 더 컸다. 또 불량률이 30% 이하인 공정의 경우 범주의 수가 10 정도만 되어도 만족할 만한 정밀도 개선 효과가 있는 것으로 나타났다. 부품치수의 표준편차가 다를 경우에 대한 추가 분석 결과는 부품의 가공정밀도가 다를 때에도 이와 같은 경향이 성립한다는 것을 보여주었다.
현실적인 부품 가공능력의 수준을 고려할 때, 잉여부품 문제뿐만 아니라 정밀도 향상이라는 측면에서도 최선 매칭 방식이 가장 유망하다고 하겠다. 다만, 최선 매칭 방식은 부품치수의 비교 횟수가 많기 때문에 최선 매칭을 찾기 위한 연산에 요구되는 시간이 더 길게 된다는 단점은 있다. 그러나 분석결과를 보면 산업현장에서의 현실적인 상황을 상정할 때 10개 정도의 부품 쌍 중에서 최선의 매칭 부품을 사용하더라도 거의 치수분할방식과 같은 수준의 정밀도 개선효과를 기대할 수 있다. 더구나 4차 산업시대로 접어들면서 향상된 컴퓨터 연산능력을 고려하면 102=100 회 정도의 치수비교가 생산속도에 영향을 주지는 않을 것이다. 또한 진보된 센서기술과 데이터 통신네트워크를 기반으로 구축된 스마트공장 환경 하에서는 생산현장 데이터가 전수 실시간으로 수집될 것이다. 따라서 향후의 산업 환경 변화를 고려할 때, 적절한 알고리즘을 컴퓨터 프로그램으로 코딩하는 정도의 투자로써 최선 매칭 방식을 현장에 구현할 수 있을 것으로 사료된다.
본 연구는 실린더와 피스톤으로 구성되는 내연엔진이나 바디와 니들로 구성되는 연료분사장치 등 두 개의 핵심 부품이 짝을 이루어 조립되는 제품의 선택조립을 고려하고 있다. 세 개 이상의 부품으로 조립되는 제품에 적용될 수 있는 치수분할방식과 통계적 매칭 방식에는 훨씬 더 다양한 방법들이 있을 수 있으며 그 중 어떤 방법이 가장 유망할 것인지 검토하는 것도 의미 있는 연구가 될 것이다. 또한 본 연구에서는 측정오차가 없는 것을 전제하고 시뮬레이션을 하였으나 측정오차가 개입될 경우 여러 가지 선택조립 방식의 실효성을 비교해보는 것도 유익한 연구가 될 것으로 기대된다.
REFERENCES
Arai, T., and Takeuchi, K. 1992. A simulation system on assembly accuracy. CIRP Annals –Manufacturing Technology 41(1):37-40.  Babu, J. R., and Asha, A. 2014. Tolerance modelling in selective assembly for minimizing linear assembly tolerance variation and assembly cost by using Taguchi and AIS algorithm. International Journal of Advanced Manufacturing Technology 75: 869-881.  Babu, J. R., and Asha, A. 2015. Modelling in selective assembly with symmetrical interval-based Taguchi loss function for minimizing assembly loss and clearance variation. International Journal of Manufacturing Technology and Management 29: 288-308.  Babu, J. R., and Asha, A. 2015. Minimizing assembly loss for a complex assembly using Taguchi's concept in selective assembly. International Journal of Productivity and Quality Management 15(3):335-356.  Boyer, D.E. 1984. Development and investigation of statistical selective assembly, Thesis, Oklahoma State University.
Boyer, D.E., and Nazemetz, J. 1985. Introducing statistical selective assembly –a means of producing high pre-cision assemblies from low precision components. Annual International Industrial Engineering Conference Proceedings: 562-570.
Burr, I. W. 1958. Some theoretical and practical aspects of tolerances for mating parts. Industrial Quality Control 15: 18-22.
Chen, M. S. 1996. Optimizing tolerance allocation for mechanical components correlated by selective assembly. International Journal of Advanced Manufacturing Technology 12: 349-355.  Desmond, D., and Setty, C. 1962. Simplification of selective assembly. International Journal of Production Research 1(3):3-18.  Fang, X. D., and Zhang, Y. 1995. A new algorithm for minimizing the surplus parts in selective assembly. Computers and Industrial Engineering 28: 341-350.  Jeevanantham, A. K., and Kannan, S. M. 2013. Selective assembly to minimize clearance variation in complex assemblies using fuzzy evolutionary programming method. ARPN Journal of Engineering and Applied Sciences 8(4):280-289.
Kannan, SM., Asha, A., and Jayabalan, V. 2005. A new method in selective assembly to minimize clearance variation for a radial assembly using genetic algorithm. Quality Engineering 17(4):595-607.  Kannan, SM, and Jayabalan, V. 2001. A new grouping method to minimize surplus parts in selective assembly for complex assemblies. Int. J. Prod. Res 39(9):1851-1863.  Kannan, SM., and Jayabalan, V. 2002. A new grouping method for minimizing the surplus parts in selective assembly. Quality Engineering 14(1):67-75.  Kannan, SM., Jayabalan, V., and Jeevanantham, K. 2003. Genetic algorithm for minimizing assembly variation in selective assembly. Int. J. Prod. Res 41(14):3301-3313.  Kannan, S. M., Jeevanantham, A. K., and Jayabalan, V. 2008. Modelling and analysis of selective assembly using Taguchi's loss function. Int. J. Prod. Res 46(15):4309-4330.  Kwon, H.M., Kim, K., and Chandra, M.J. 1999. An Economic Selective Assembly Procedure for Two Mating Components with Equal Variance. Naval Research Logistics 46: 809-821.  Mansoor, E. 1961. Selective assembly –its analysis and applications. International Journal of Production Research 1(1):13-24.  Matsuura, S., and Shinozaki, N. 2007. Optimal binning strategies under squared error loss in selective assembly with measurement error. Communications in Statistics- Theory and Methods 36: 2863-2876.  Matsuura, S., and Shinozaki, N. 2010. Optimal binning strategies under squared error loss in selective assembly with a tolerance constraint. Communications in Statistics- Theory and Methods 39: 592-605.  Mease, D., Nair, V. N., and Sudjianto, A. 2004. Selective assembly in manufacturing: statistical issues and optimal binning strategies. Technometrics 46: 165-175.  Nelson, W. 1967. The truncated normal distribution –with applications to component sorting. Industrial Quality Control 24: 261-271.
Pugh, G.A. 1986. Group formation in selective assembly. SME Ultrtech Conference Proceedings, 2.117-123.
Pugh, G.A. 1986. Partitioning for selective assembly. Computers and Industrial Engineering Conference Proceedings, 175-179.
Pugh, G.A. 1992. Selective assembly with components of dissimilar variance. Computers and Industrial Engineering 23: 487-491.  Rabinovich, L. A. 1968. Improving the characteristics in selective assembly. Russian Engineering Journal 48: 54-59.
Rabinovich, L. A., and Kesoyan, A. G. 1980. Investigating the rational sorting accuracy for selective assembly of precision units. Russian Engineering Journal 60(10):50-53.
Rubenchik, V. Ya, Mentov, K. V., and Novikov, V. V. 1979. Automatic sorting of rings by size prior to selective assembly. Measure Tech 22(1):71-73.  Zhang, Y., Yin, Y., and Yang, M. 2010. A new selective assembly approach for remanufacturing of mating parts. Proceedings of 40th International Conference on Computers and Industrial Engineering, 1-6.
|
|