1.서 론
품질향상을 위한 설계기반 품질고도화(quality by design)는 품질이 제품으로 설계되어야 한다는 최초의 Juran(1992)의 개념이 확대되어 최근에는 실험계획법을 근간으로 하는 실험설계와 수학적 모델에 기반 한 디자인 스페이스(design space)를 개발하게 되었다. 디자인 스페이스 내에서의 제조는 품질 목표 사항(QTPP)과 주요 품질 특성(CQA)이 만족된 제품이 제조 될 수 있도록 보장한다. 즉, 설명변수들의 흔들림이 발생하여 공정조건이 최적조건에서 약간 벗어나도 디자인 스페이스 내에서 제조가 된다면 품질 목표 사항이 만족된 제품이 생산되지만, 디자인 스페이스를 벗어나서 생산된 제품은 품질을 보장받지 못하게 된다. 최근에 의약품 개발에서도 체계적인 의약품 개발을 위한 가이드 라인으로 디자인 스페이스 개념이 적용되고 있다.(ICH Q8)
디자인 스페이스는 품질특성의 허용한계인 공차(tolerance) 개념을 이용하여 생산된 제품의 품질 목표범위 안에 공정 조건에서 제조된 제품의 tolerance 신뢰구간의 포함 여부에 따라서 정의된다. Tolerance 신뢰구간은 신뢰수준 (1-α)에서 모집단의 P%가 신뢰구간에 포함되는 것인데, 보통 P = 0.99로 정의하여 디자인 스페이스에 속한 공정조건에서 제품이 제조되면 제품의 99%는 품질이 보증 받게 된다. 따라서, 2개 이상의 품질관련 반응 변수들이 있을 경우 이들 tolerance 신뢰구간에 대한 교집합으로 구축된 디자인 스페이스가 공집합이 되지 않아야 하며 그 안에 최적조건이 있어야 품질을 보장하는 공정조건들이 생긴다. 이를 위해 산포가 작은 정밀한 tolerance 신뢰구간이 구축되어야 하는데, 이는 실험설계를 할 때 적절한 실험 계획 및 실험의 크기를 결정하여 예측치의 표준편차를 적정수준으로 줄이는 것과 연관이 있다. 정종희 등(2019)은 반응표면분석에서 디자인 스페이스 구축을 위한 효율적인 실험설계를 찾기 위해 FDS(Fraction of Design Space) 그림을 이용하는 방법을 소개했다. FDS 그림은 Zahran 등(2003)이 제안한 방법으로 총 설명변수 영역에서 지정된 예측치의 표준편차보다 작거나 같은 설명변수 영역에 대한 비율을 그린 그래프이다. 정종희 등(2019)에서는 가정된 이차모형에 대한 반응표면분석으로 실용적인 실험계획인 회전가능 중심합성계획의 요인점, 축점, 중심점을 반복하여 각 반복수마다 FDS 비율이 80%이상이 되는 단위 표준편차 크기 당 tolerance 신뢰구간 기준의 최소한의 폭(d2)을 찾고, 그 폭이 4.5이하 일 때를 효율적인 실험계획으로 제안하였다. 효율적인 실험계획의 결과를 보면, 축점보다는 요인점을 반복할 때 d2 값이 작아지고, D-효율성도 좋아지게 됨을 알 수 있었다.
본 논문에서는 혼합물 분석에서 디자인 스페이스 구축을 위해 FDS 그림을 이용한 효율적인 실험을 설계하는 방법에 대해 제안하고자 한다. 혼합물 분석의 설명변수들은 혼합물의 구성 성분의 비율이다. 즉, 반응변수의 평균이 구성 성분의 비율만의 함수가 되고 혼합물의 양에는 영향을 받지 않는 반응표면분석의 특수한 경우이다. q개 성분의 혼합물에 있어서 xi를 i번째 성분의 혼합비율이라고 하면, 혼합비율들은 수식 (1)과 같은 관계식을 만족해야 하기에 혼합물 분석의 실험 공간은 q-1차원 심플렉스(simplex) 공간이 된다.
이러한 혼합물 분석을 활용하는 분야는 제약업에서 지효성 알약의 혼합비율이나 석유화학분야에서 가솔린의 혼합비율, 반도체와 LCD 분야에서의 식각용액의 혼합비, 식음료업에서의 과즙음료의 혼합비율의 결정, 표백력과 세탁력을 최적화하는 세재의 혼합비 등 광범위하다.
본 논문에서는 가정된 이차모형에 대한 정준 다항 회귀 모형(canonical polynomial)에 대해서 디자인 스페이스 구축을 위해 심플렉스 공간 영역에서 꼭지점(Vertex), 모서리점(Centroid of Edge), 축점(Axial), 중앙점(Center)을 반복하여 각 반복수마다 FDS 비율이 80%이상이 되는 단위 표준편차 크기 당 tolerance 신뢰구간 기준의 최소한의 폭인 d2를 찾아 비교하여 d2를 가장 작게 하는 효율적인 실험설계를 찾고자 한다. FDS 비율이 최소한 80%이상이 되도록 선택한 이유는 정종희 등(2019)에서도 언급하였듯이 Whitcomb(2008)이 예측치의 표준편차가 주어졌을 때에 FDS 비율이 최소한 80%이상이 되도록 실험의 설계 및 크기를 결정하라는 실무적 제안에 따라서 이다. 특히, d2가 4.5를 상회하는 실험설계에 대해서 축차적 접근방법으로 d2를 축소하여 4.5이하가 될 수 있는 실험점별 반복수를 찾고자 한다. d2 = 4.5로 선택된 이유은 6 시그마(six sigma) 경영에서 평균이 1.5 시그마 이동이 일어난 경우에 규격 한계 까지의 거리가 4,5 시그마이고, 불량률 0.000679%로 공정능력이 매우 우수함을 나타내는 지표에 해당되기 때문이다.
그래서 2장에서는 혼합물 실험설계에 대해 구체적으로 설명하고, 3장에서는 성분수별 혼합물 실험설계에서 반복에 따른 FDS 비율이 80%이상이 되는 단위 표준편차 크기 당 mean과 tolerance 신뢰구간 기준의 최소한의 폭을 찾아 제시하며, d2가 4.5를 상회하는 경우에 축차적으로 d2를 축소하여 4.5이하가 될 수 있는 반복수를 찾아 제시한다. 4장에서는 사례분석을 통해 디자인 스페이스를 구축하여 그 안에 최적조건이 포함되는지를 살펴보는 일련의 과정을 소개한다.
2.혼합물 실험설계
q개의 성분으로 구성된 혼합물 실험 공간은 q-1차원 심플렉스 공간이 된다. 또한, 수식 (1)과 같은 제약 조건에 따라 가정된 이차모형은 수식 (2)와 같이 정준 다항 회귀 모형이 된다.
예를 들어, q=3개의 성분으로 구성된 혼합물 실험을 가정해 보자. 실험 공간은 Figure 1의 (a)와 같이 2차원의 심플렉스 공간이고, 가정된 이차모형을 위한 실용적인 실험설계는 Figure 1의 (b)와 같이 {3,2} 심플렉스 격자법 설계에 축점 (xi = xj = 1/6, xk = 2/3)과 중앙점 (xi = xj = xk = 1/3)이 추가된 경우이다.
꼭지점, 모서리점, 축점, 중앙점인 4개의 부분으로 이루어진 실험설계로 설계행렬(design matrix)이 결정되고, Figure 1의 (a)에 주어진 2차원 심플레스 공간 내의 한 점 x0를 선택하면 그 점에서 실험의 크기 n에 대하여 조정되지 않은 예측치 분산(UPV: unscaled prediction variance)의 제곱근 U P V
단, X는 설계행렬(design matrix)이다.
정종희 등(2019)에서 U P V
– x0에서의 모평균 반응값에 대한 (1-α)% 신뢰구간 기준
– (1-α)% 신뢰수준에서 모집단의 P%가 신뢰구간에 포함되는 tolerance 신뢰구간 기준
3.효율적인 실험설계
FDS 관점에서 효율적인 실험설계를 제안하기 위해 혼합물 실험설계의 구성성분의 개수인 q가 3, 4, 5 인 경우에 FDS 비율이 80%이상이 되는 단위 표준편차 당 mean과 tolerance 신뢰구간 기준의 최소한의 폭인 d1, d2를 찾아 비교하고, 효율적인 실험설계를 추천하고자 한다. 이를 위해 제 1종 오류의 확률 α는 0.05, 표준편차 s는 1, toler-ance 신뢰구간을 위한 모집단의 비율 P는 0.99로 가정한다. d1, d2의 값이 작을수록 FDS 관점에서 효율적인 실험설계가 된다. 또한 제시되는 실험설계의 효율성을 비교하기 위해 D-효율(scaled D-optimal efficiency) 값도 제시하여 비교하는데, 이때 D-효율성은 수식 (6)에 정의된 것처럼 관측치 1개당 효율성을 정의하고 있고, 작은 값일수록 효율적인 실험설계에 해당한다.
q개의 성분일 경우 가정된 이차모형을 위한 혼합물 실험설계는 {q,2} 심플렉스 격자법을 기본 설계로 한다. q개의 꼭지점, qC2개의 모서리점, q개의 축점, 1개의 중앙점을 형성할 수 있으며 각 점에서 완전(또는 부분) 반복으로 실험의 크기를 증가시킬 수 있다. 축점과 중앙점은 이차모형을 가정할 때 포함하지 않아도 되나, 축점과 중앙점이 추가되면 심플렉스 공간 내부의 정보가 추가될 수 있으며 특별 삼차모형으로 모형 확장이 가능하여 실용적인 실험설계가 가능해진다. 예를 들어, q = 3인 경우, 간결한 실용적인 실험설계는 {3,2} 심플렉스 격자법에 중앙점이 추가된 실험설계로 실험의 크기는 꼭지점 3개, 모서리점 3개, 중앙점 1개로 7개가 된다. 여기서 꼭지점 전체를 한번 반복하면 실험의 크기는 10개가 된다. 물론 모서리점을 한번 반복해도 10개가 된다. 이런 방식으로 각 영역들을 반복하면 동일한 실험의 크기에서도 서로 다른 후보 실험설계들을 찾을 수 있다. 동일한 실험의 크기인 경우 어떤 형태의 후보 실험점을 반복하는 것이 더 효율적인지 찾아보고자 Table 1과 같이 축차적인 방법으로 실험점을 추가하여 효율성을 비교한다. 실험설계는 실험계획에 특화된 소프트웨어인 Design Expert 12를 통해 생성하였으며 FDS 비율 및 d1, d2, D-효율성 지표는 정종희 등(2019)에서 개발한 R 프로그램을 이용하여 산출하였다.
Table 1.
Minimal d1:d2 for mixture designs
Table 1의 (a)에는 성분의 수 q = 3인 경우에 실험의 크기 n, 18 ≤ n ≤ 21 에 대하여 FDS 비율이 80%가 되는 단위 표준편차 당 d2가 가장 작은 실험설계를 찾아 영역별로 반복수를 정리한 실험설계가 ‘Space Type’으로 표시되어 있다. n = 18인 경우는 꼭지점 6개(2회 반복), 모서리점 9개(3회 반복), 중앙점 3개(3회 반복)인 설계의 d2가 4.94로 다른 조합에 비해 가장 작다는 것을 의미한다. n = 19인 경우에는 꼭지점 6개(2회 반복), 모서리점 12개(4회 반복), 중앙점 1개인 실험설계를 추천한다. n = 20, 21인 경우에는 n = 19의 실험설계에서 중앙점의 수를 각각 증가시킨 실험설계이다. 실험의 크기 n = 18인 경우 실험자료의 분석을 생각해 보자. 추천된 d2가 4.94인 실험설계로부터 얻어진 실험자료의 분석 결과, 디자인 스페이스가 공집합인 경우에 해결책의 하나는 이 보다 더 작은 d2값을 갖게 하기 위해 축차적으로 추가 실험을 실시하는 것이다. 이럴 경우 어떤 영역의 점을 반복해야 하는지 알아보기 위해 추가점 3개를 각 영역별로 반복했을 때의 d1, d2와 D-효율성을 찾아 정리하였다. 또한, I-optimal 실험설계로 심플렉스 영역의 4가지 형태의 모든 실험점들을 후보실험점으로 하여 3개의 추가점을 찾은 결과도 같이 보여주었다. 찾아진 I-optimal 실험설계는 모서리점을 3개 추가하도록 나와서 결과값들이 모서리점 추가와 동일하다. 이는 실험의 크기 n = 19,20,21개 일 때도 마찬가지이다. 결론적으로는 현 실험설계에서 모서리점을 한 번 더 반복하는 것이 다른 영역을 반복하는 것보다 d2값이 작아져 FDS 관점에서 더 효율적이라는 것을 알 수 있다. 또한, 꼭지점을 반복하면 d2값이 별로 차이가 없는 반면에 D-효율성 관점에서 가장 효율적이 된다. 따라서 실험자의 선호에 따라서 모서리점 혹은 꼭지점을 반복하는 실험설계를 선택할 수 있다. 축점을 반복하면 FDS 지표인 d2나 D-효율성도 비효율적이 되나 축점으로 부터 얻고자 하는 심플렉스 내부 정보나 특별 삼차모형 확대 등이 가능하다는 장점이 있다.
Table 1의 (b)는 성분의 수 q = 4인 경우에 해당하는 데, 기본설계가 꼭지점과 축점의 수는 4개이지만 모서리점은 6개로 구성되어 있다. 따라서, 추가 실험점을 4개와 6개일 때로 구분하였고, 추가 실험점 4개일 때의 모서리점은 후보 실험점을 6개의 모서리점만으로 제한한 경우에 I-optimal 기준에서 최적으로 하는 모서리점들을 선택하여 모서리 점들의 부분 반복이 되도록 하였다. 마찬가지로 추가점 6개인 경우의 꼭지점과 축점은 후보 실험점들을 각각 꼭지점과 축점으로만 제한한 경우에 I-optimal 기준에서 최적으로 하는 꼭지점과 축점을 선택하여 완전+부분 반복이 되도록 하였다. 또한, I-optimal 설계는 성분의 수 q = 3인 경우와 마찬가지로 모든 후보점들을 대상으로 선택한 결 과이다. 실험의 크기 n, 22 ≤ n ≤ 25에 대하여 d2값이 가장 작은 설계들을 찾은 결과 실험의 크기 n = 22인 실험설계는 꼭지점 4개(1회반복), 모서리점 12개(2회반복), 축점 4개(1회반복), 중앙점 2개이다. 실험의 크기 n = 23인 실험설계는 성분의 수 q = 3인 경우와 유사하게 모서리점 18개(3회반복)로 늘어나는 대신 축점이 없어지고 중앙점은 1개로 선택된다. n = 24, 25인 경우에는 n = 23의 실험설계에서 중앙점의 수를 하나씩 각각 증가시킨 실험설계이다. 성분의 수 q = 4인 경우에 축차적으로 추가 실험점을 찾은 결과, q = 3인 경우와 동일하게 모서리점을 추가하는 것이 FDS 관점에서는 가장 효율적이라는 결과를 얻을 수 있다.
Table 1의 (c)는 성분의 수 q = 5인 경우에 해당한다. 기본설계에서 꼭지점과 축점의 수는 5개이지만 모서리점은 10개로 구성되어 있다. 성분의 수 q=4인 경우와 마찬가지로 축차적으로 실험점을 추가할 때 추가 실험점의 수가 5개인 경우와 10개인 경우로 나누어 부분 또는 완전+부분 반복으로 추가되는 점에 대한 d2를 비교하면 모서리점 추가 실험설계와 I-optimal 설계가 큰 차이가 없음을 알 수 있다. 실험의 크기 n, 26 ≤ n ≤ 30에 대하여 d2값이 가장 작은 설계들을 찾은 결과 실험의 크기 n = 26인 실험설계는 꼭지점 5개(1회반복), 모서리점 20개(2회반복), 중앙점 1개이다. 실험의 크기 n, 27 ≤ n ≤ 30인 경우에는 n = 26의 실험설계에서 중앙점의 수를 하나씩 각각 증가시킨 실험설계이다. 이들에 대하여 축차적으로 추가 실험점을 찾은 결과, q = 3, 4인 경우와 동일하게 모서리점을 추가하는 것이 FDS 관점에서는 효율적이라는 결과를 얻을 수 있다. 단, 추가 실험점의 수가 5인 경우에는 q = 3, 4인 경우와 유사하게 꼭지점을 반복하면 d2값이 별로 차이가 없는 반면에 D-효율성 관점에서 가장 효율적이어서 꼭지점의 반복도 고려할 수 있지만, 추가실험점의 수가 10인 경우에는 모서리점을 추가하는 것이 FDS 관점에서는 효율적이다.
정종희 등(2019)은 반응표면분석에서 d2 ≤ 4.5 인 설계를 최종적으로 효율적인 설계로 추천하였다. 혼합물 분석에서도 동일한 기준을 적용해 보면, 성분 개수 3개인 경우는 실험의 크기 n ≥ 23, 성분 개수 4개는 n ≥ 28, 성분 개수 5개는 n ≥ 33인 경우에 해당된다.
4.simulation 사례
4.1 성분 개수 3개 – 이차모형
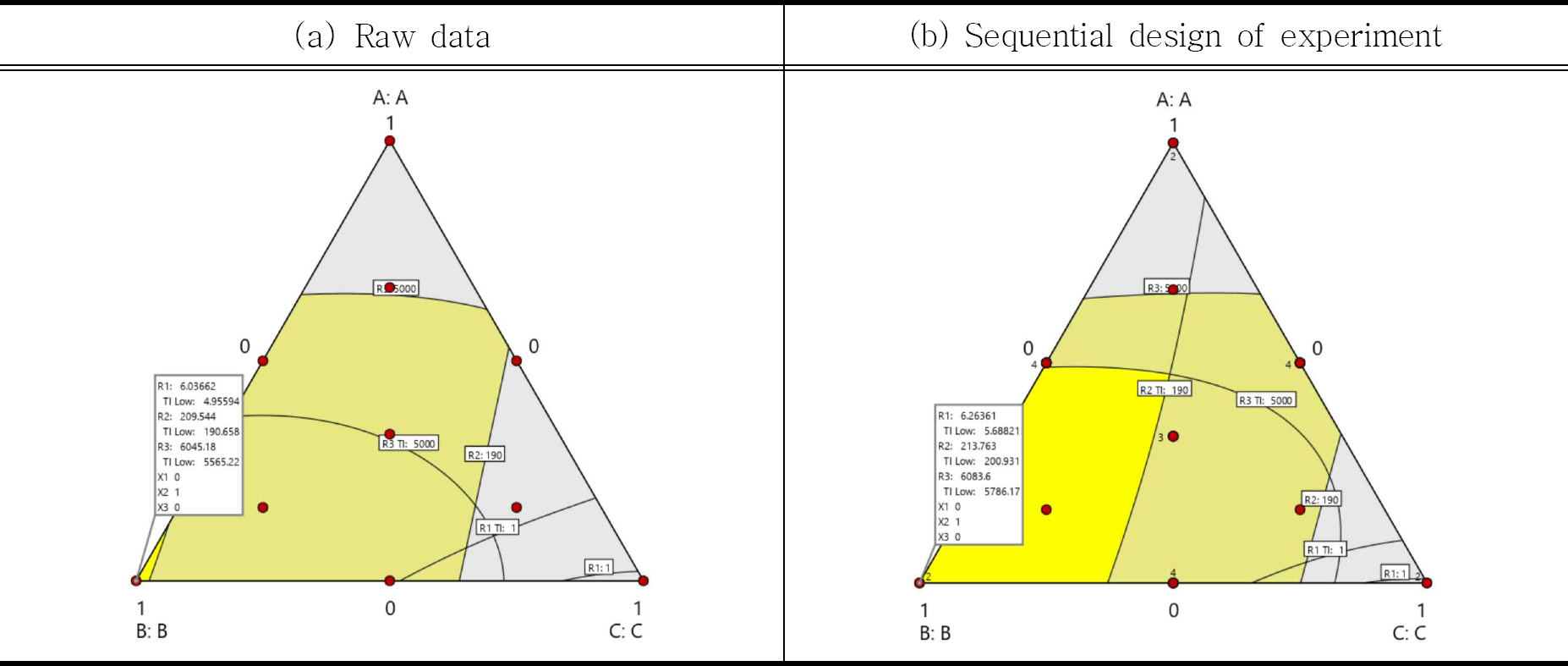
Koons 등(1985)은 플라스틱 파이프를 만드는데 사용되는 물질인 ABS(acrylonitrile butadiene styrene)의 배합과 관련된 실험을 하였다. ABS는 일반적으로 폴리 부타디엔(x1)과 스티렌 아크릴로 니트릴(x2)으로 만들어 지는데, 석탄-타르피치(x3)가 추가되어 ASTM 사양을 충족하는 물리적 특성을 갖는 파이프를 형성할 수 있는지 여부를 결정하기 위해 혼합물 실험을 실행하였다. 반응변수는 y1(Izod impact strength, 범위 >1, 망대특성), y2(deflection temperature under load, 범위 > 190, 망대특성), y3(yield strength, 범위> 5000, 망대특성)로 3개이다. 꼭지점, 모서리점, 축점, 중앙점을 각각 1회 반복한 기본 설계로 하여 총 실험수는 10개이며, 실제 성분비를 0과 1사이의 pseudo-component로 나타내어 표시하면 Table 2와 같이 실험 데이타가 주어진다.
Table 2.
Raw data for example 1
Table 2를 이용하여 각각의 반응변수에 대해서 적절한 모형을 찾은 결과가 수식 (7)에 주어지고, 각각의 반응변수에 대한 모형평가 통계량은 y1 모형은 Adj - R2 = 0.994, MSE = 0.0284 y2는 Adj - R2 = 0.834, MSE = 15.35 y3은 Adj - R2 = 0.975, MSE = 5599.96을 얻었다.
반응변수 목표 범위 안에서 동시 최적화를 해보면, 성분 비율이x1 = 0, x2 = 1, x3 = 0일 때 y ^ 1 y ^ 2 y ^ 3
Table 3.
Additional data for sequential design of experiment
앞서 진행된 방법과 동일하게 이차 모형식을 적합하여 반응변수 목표 범위 안에서 최적화를 해보면, 성분 비율이 x1 = 0, x2 = 1, x3 = 0인 것이 최적의 해가 되고 Figue 2의 (b)와 같이 디자인 스페이스 안에 최적의 해가 포함된다. 또한, 디자인 스페이스 크기가 더 커졌음을 확인할 수 있다. 따라서, 최적의 성분 비율에서 품질을 생성하다가 흔들림이 발생하더라도 디자인 스페이스 내라면 품질의 만족도에는 큰 영향을 주지 않을 것이라 예상할 수 있다.
4.2 성분 개수 3개 – 특수 삼차모형
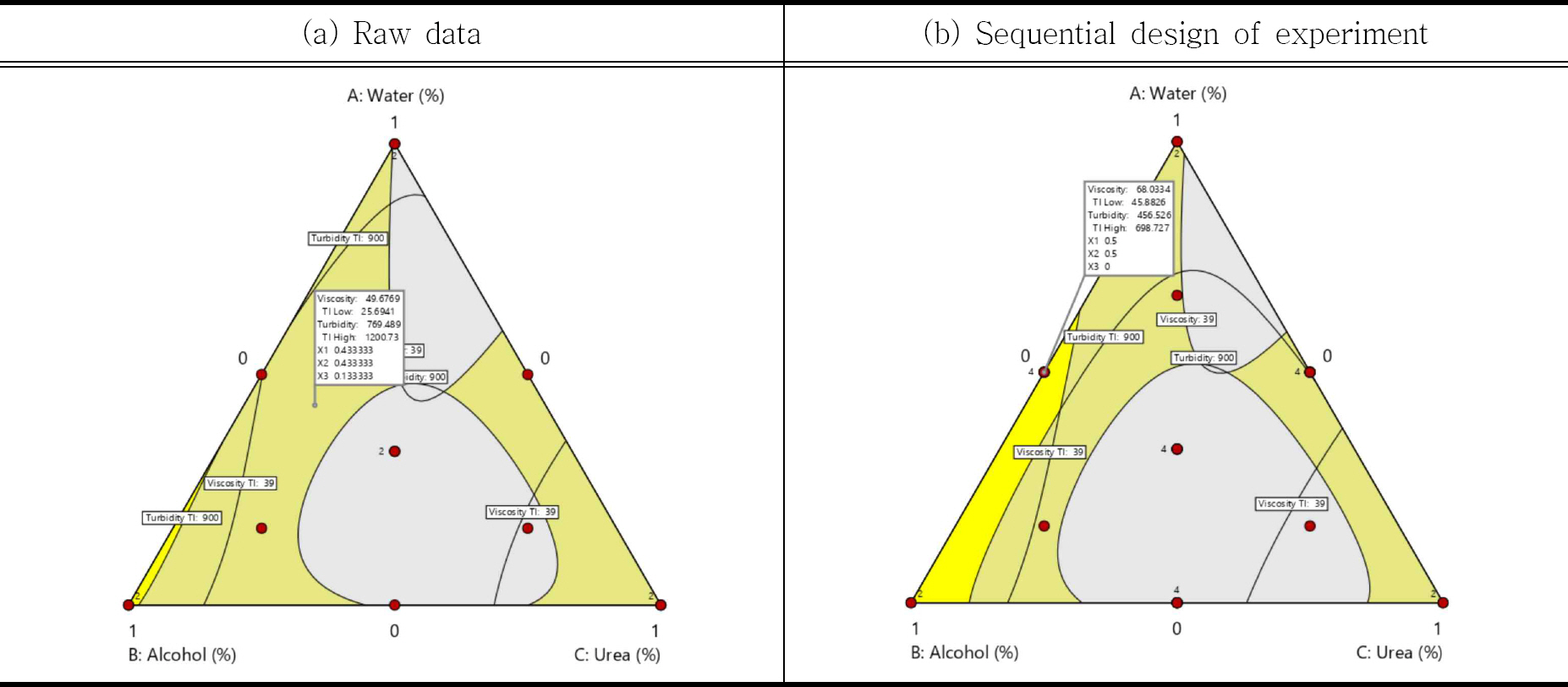
Design Expert 사용 지침서에(Stat-Ease 2019) 예제로 있는 세제의 점도(viscosity, y1, 범위 39∼48, 망대특성)와 혼탁도(turbidity, y2, 범위 800∼900, 망소특성)를 반응값으로 하고 물(x1), 알코올(x2), 요소(x3) 3가지 성분 비율을 설명변수로 하는 혼합물 실험의 경우를 살펴보고자 한다. 꼭지점 6개(2회반복), 모서리점 3개(1회반복), 축점 3개(1회반복), 중앙점 2개(2회반복)로 총 실험수 14개이며 실제 성분비를 0과 1사이의 pseudo-component로 나타내어 표시된 실험 데이터는 Table 4에 정리되어 있다.
Table 4.
Raw data for example 2
Table 4를 이용하여 적절한 모형을 찾은 결과, y1은 이차 모형식에 적합되나, y2는 특수 삼차 모형식(special cu-bic)에 적합되어 수식 (8)과 같은 예측치가 얻어졌다. 이때 y1의 모형 평가 통계량은Adj - R2 = 0.976, MSE = 29.70, y2는 R2 = 0.853, MSE = 8751.45을 얻었다.
반응변수 목표 범위 안에서 동시 최적화를 해보면, 성분 비율이 x1 = 0.433, x2 = 0.433, x3 = 0.133일 때 y ^ 1 y ^ 2
Table 5.
Additional data for sequential design of experiment
축차적으로 얻어진 데이터를 합하여 분석하면 성분 비율이 x1 = 0.5, x2 = 0.5, x3 = 0인 것이 최적의 해가 되고 Figure 3의 (b)와 같이 최적의 해가 포함되면서 더 넓어진 디자인 스페이스를 구축할 수 있다.
5.결론
반응표면분석의 특수한 형태인 혼합물 분석에 있어서 실험의 목적이 품질 고도화에서 디자인 스페이스의 효율적인 구축이라면, 여러 실험설계들의 비교를 위해 FDS 비율을 이용할 것을 제안한다. 잘 알려진 실용적인 혼합물 실험설계는 q개의 구성 성분의 혼합물 실험공간인 q-1차원 심플렉스 공간상의 4가지 형태의 실험점인 꼭지점, 모서리점, 축점, 중앙점으로 구성된 실험 설계이다. 각 형태의 실험점의 반복을 통해 효율적인 실험설계를 선택할 수 있는 여러 후보 실험설계들을 만들어 낼 수 있다. 이들 중에서 가정된 이차모형에 대한 FDS 비율이 80%이상이 되는 단위 표준편차의 크기 당 tolerance 신뢰구간 기준의 최소한의 폭인 d2가 가장 작은 설계를 효율적인 설계라고 제안한다. 다른 영역에 비해 모서리점을 반복할 때 d2값이 작아짐을 알 수 있고, 이는 특수 삼차 모형을 가정할 때도 동일함을 예제를 통해 살펴 보았다. 본 논문에서 축차적인 방법으로 디자인 스페이스를 더 넓게 구축하는 과정을 설명한 예제들을 바탕으로 혼합물 분석이 필요한 연구원들도 품질 고도화 관점에서 효율적인 실험설계를 구축할 수 있을 것이라 기대한다.