1. 서 론
FMEA(Failure mode and effect analysis)는 중요고장원인에 대한 예방조치를 취하기 위해 위험을 평가하고 조치의 우선순위를 결정하는데 효과적인 도구이다. FMEA에서 위험평가에 관련된 기존의 연구들에 대해서는 Liu 등(2013)이 종합하여 정리하였다. 그러나 전통적인 FMEA에서는 하나의 고장원인이 하나의 고장유형에 관련된 경우를 주로 취급하고 있다. 그런데 하나의 원인이 둘 이상의 고장 유형을 일으킨다면 그로 인한 영향이 단일 고장유형을 유발하는 경우보다 더 심각한 결과를 초래하게 될 가능성이 크다. 그럼에도 불구하고 기존의 FMEA 절차에서는 공통고장원인에 대한 처리방안이 구체적으로 제시되어 있지 않다. 또한 기존의 연구 중에도 공통고장원인의 취급방법에 관련된 것은 별로 없고 그 결과에 따른 신뢰도 혹은 위험평가에 대한 연구가 대부분이다.
공통원인고장에 관련된 연구들은 주로 원자력 발전 분야에서 이루어졌으며 FTA(Fault Tree Analysis), RBD(Reliability Block Diagram) 등의 도구들을 이용하여 고장원인보다는 결과에 대한 위험 혹은 신뢰성평가에 초점이 맞추어졌다. Mosleh 등(1988)은 원자력발전시스템의 위험 및 신뢰도 평가에서 공통원인고장의 영향을 포함시키기 위한 기본 골격을 제시하였다. Parry(1991)는 공통원인고장의 정량적 분석절차에 대한 기존의 연구들을 검토하고 더 일관성 있고 구체적인 고장메커니즘 규명의 필요성을 기술하였다. Rasmuson과 Mosleh(2007)은 공통원인고장에 대한 이전의 연구 이력을 정리하였다. Kelly와 Rasmuson(2008)은 원자력 발전 시스템 운영에 따른 확률적 위험평가에 있어서 미국원자력위원회가 채택하고 있는 공통원인고장에 대한 접근방법을 기술하였다. Jones(2016)은 공통원인고장이 있을 경우 신뢰도 평가 모형과 고신뢰도 달성에 주는 영향을 정리하였다. Kreuser와 Johanson(2017)은 공통원인고장 데이터의 국제적인 공유프로젝트를 통해 분석된 결과를 정리하였다.
한편, FMEA에서 공통원인고장에 대해 언급되고 있는 연구는 Childs와 Mosleh(1999), Sankar와 Prabhu(2001) 등 몇 편에 불과하다. 다만, 병원의 진료서비스 분야에서는 FMEA를 적용하여 공통원인분석(CCA: Common Cause Analysis)이라는 주제로 최근 연구된 사례가 발표되고 있다. Clapper와 Crea(2010) 및 McGinley(2010)은 오하이오 주의 18개 병원 그룹인 OhioHealth의 사례를 소개하였고 Browne 등(2018)은 필라델피아의 어린이 병원을 대상으로 한 연구결과를 정리하였다. 이와 같은 사례들은 서비스 시스템에서도 공통원인으로 인한 문제들이 많이 있을 수 있음을 보여준다.
FMEA는 기본적으로 시스템의 개발 혹은 설계 단계에서 있을 수 있는 문제들을 예견하여 그 원인들을 식별하여 사전에 조치함으로써 신뢰도가 높은 시스템을 구현하기 위해 고안된 도구이다. 즉, 고장이나 문제가 발생한 후에 조치를 어떻게 할 것인가가 아니라 사전에 예방하기 위한 방안을 효과적으로 찾기 위한 도구이다. 문제나 고장 발생을 방지하기 위해서는 가능한 원인들을 식별하고 원인에 대한 예방조치를 취해야 한다. 그런데 어느 조직에서나 예산을 포함하여 가용한 인적 물적 자원에는 한계가 있으므로 모든 가능한 원인에 대해 빠짐없이 조치를 취하는 것은 현실적으로 불가능하기 때문에 각 원인에 대해 조치해야 할 우선순위를 평가할 수 있어야 한다. 이와 같이 고장이나 문제의 원인에 대해 사전조치의 우선순위를 부여하는 데 유용한 척도가 FMEA의 RPN(Risk Priority number)이다. 그러나 전통적인 FMEA에서는 공통고장원인에 대한 RPN 평가 방식을 따로 제시하고 있는 것은 아니므로 기존의 방식에 따를 수밖에 없다. 만약, 단일 고장원인과 공통고장원인의 RPN을 기존 방식으로 계산하여 비교한다면 공정한 비교라 할 수 없게 된다. 예로서 단일 고장원인의 RPN이 360이고 두 고장유형을 유발하는 공통고장원인에 대해 두 가지 고장유형의 심각도를 고려하여 RPN을 계산한 결과 336, 240 두 값을 얻었다고 하자. 이 때 360이 336보다 크다고 하여 단일 고장원인의 위험이 더 크다고 판정한다면 항상 올바른 결정이라고는 보기 어려울 것이다. 만약 두 고장유형이 동시에 발생한다면 공통고장원인의 위험이 단일 고장원인보다 더 크게 될 경우가 많기 때문이다.
본 연구에서는 공통고장원인이 존재할 경우 그에 기인된 모든 고장들의 영향을 종합하여 각 공통고장원인에 대해 하나의 RPN을 산출함으로써 모든 원인들에 대해 객관적인 비교가 가능하도록 하는 절차를 제시해보고자 한다. 이 논문의 2절에서 공통원인고장이 있을 때 기존 FMEA 방식을 적용할 경우의 문제점을 살펴보고, 3절에서 공통고장원인에 대한 심각도 결정방법과 수정된 FMEA 실시 절차, 그리고 4절에서 예제와 함께 몇 가지 논점을 제시하고 5절에서 결론을 맺는다.
2. 기존 FMEA 방식의 검토
이 절에서는 종속고장과 공통원인고장을 소개하고 기존의 분석 모형을 검토하고 그 한계점을 살펴본다.
2.1 종속고장과 공통원인고장
둘 이상의 고장 유형이 서로 독립적으로 발생하지 않고 어떤 원인에 의해 영향을 받을 경우 종속고장(dependent failure)이라고 한다. Figure 1의 (a)와 (b)에서 두 고장 유형 F1과 F2가 서로 종속적임을 확인할 수 있다. 즉, (a)와 (b)에서 P ( F 1 ) = P ( F 2 ) = 2 / 5 로서 P ( F 1 ∩ F 2 ) = 1 / 5 ≠ 4 / 25 = P ( F 1 ) P ( F 2 )
Figure 1에서 F1과 F2는 원인 E3를 공유하고 있는데 여기서 E3를 공통고장원인(common failure cause)라 하고 F1과 F2를 공통원인고장(common cause failures)이라 한다. 공통원인고장은 종속고장의 특수한 형태라 할 수 있다. 그런데 (a)의 경우는 공통원인 E3가 일단 발생하고 나면 F1과 F2는 독립적으로 발생하는 상황을 보여주고 (b)는 그렇지 않은 상황을 보여준다. 이와 같이 공통원인고장이라 하더라도 상황에 따라 발생 메커니즘이 다를 수 있으므로 이를 분석하는 모형도 달라야 할 것이다.
2.2 공통원인고장의 분석모형
FTA에서 공통원인고장을 포함하여 PRA(Probabilistic Risk Assessment)가 시작된 것은 1967년 아폴로 1호 화재사건발생 후부터였다. 1979년 드리마일 아일랜드 방사능 누출 사고 후 원자력발전 분야에서도 PRA를 채택하였고 1970년대부터 1980년대에 걸쳐 공통원인고장 분석을 위한 수학적 모형이 개발되었다. 여기서는 Rausand and Hoyland(2004)와 Jones(2016)을 참고하여 대표적으로 베타인자모형, MGL(Multiple Greek Letter) 모형, 알파인자모형에 대해서만 요약하여 설명한다.
(1) 베타인자 모형
전체 고장 중 일부는 공통원인에 의해 발생하고 나머지는 독립적인 원인에 기인된다고 가정한 모형이다. 즉, 전체 고장 중 β의 비율만큼은 공통고장원인에 기인된다고 보고 분석하는 것이다. 병렬중복으로 시스템의 고장확률을 낮추고자 할 때 원 고장확률에 β를 곱한 값 이하로 낮출 수 없게 된다. 예를 들어 고장확률이 0.01인 부품을 병렬중복하면 공통고장원인이 없을 경우에는 0.0001로 낮아지게 되겠지만 β인 공통고장원인이 있다면 0.001보다 작을 수 없게 된다. 이 경우 정상적인 병렬구조에 비해 10배 이상의 고장확률을 갖게 되는 것이다. 중복부품 수가 많아질수록 그 차이가 두드러지게 된다.
(2) MGL 모형
셋 이상 부품의 중복구조로 이루어진 시스템에서 첫 부품 고장이 발생했을 때 두 번째 부품이 고장 날 확률 β, 첫 번째와 두 번째 부품이 고장 났을 때 세 번째 부품이 고장 날 확률 γ등과 같이 조건부 확률을 필요한 만큼 그리스 문자로 나타내어 분석하는 모형이다. 베타인자 모형의 확장된 형태이므로 확장 베타모형 혹은 다중 베타모형이라고도 한다.
(3) 알파인자 모형
다중고장의 모든 가능한 조합을 모형에 포함시켜 분석한다. Q k ( m ) m k m k Q k ( m ) ∑ k = 1 m m k Q k ( m )
알파인자 αk(m)은 m 중 k고장으로 인한 시스템 고장의 비율이다. 만약 세 개의 동일한 부품으로 구성된 병렬구조 시스템을 고려하면, 하나의 부품이 고장 날 확률은 3Q1(3)이고 부품 둘 혹은 셋이 고장 날 확률은 각각 3Q2(3), Q3(3) 이다. 따라서 셋 중 적어도 하나 이상 고장일 확률은 Qss=3Q1(3)+3Q2(3)+Q3(3)이고 α1(3)=3Q1(3)/Qss, α2(3)=3Q2(3)/Qss, α3(3)=Q3(3)/Qss이다. 이 때, α1(3)은 개별적인 독립고장에 대응되고 α2(3), α3(3)두 부품 및 세 부품의 종속적인 공통원인고장이 된다.
2.3 기존의 심각도 및 RPN 산출 방식의 한계
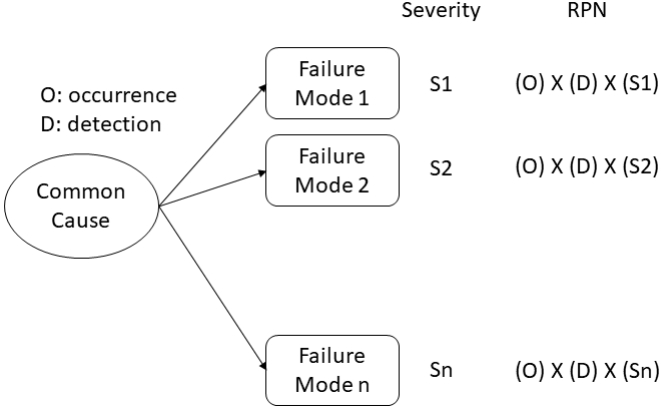
시스템 FMEA는 기본적으로 시스템 기능에 악영향을 고장원인들을 사전에 찾아 조치함으로써 문제를 예방하는데 그 목적이 있으므로 원인에 대한 조치우선순위를 합리적으로 결정하는 것이 중요하다. 그런데 기존의 FMEA 절차를 따르게 되면 공통고장원인이 있는 상황에서는 원인의 중요도를 공정하게 비교할 수 없다. 왜냐 하면 기존의 FMEA에서는 고장유형을 식별하고 그에 대한 원인을 도출하여 RPN을 계산하기 때문에 각 고장유형별 원인에 대한 RPN값이 따로 산출되기 때문이다. 공통고장원인이 있을 경우에는 같은 원인이 여러 고장유형에 관계되므로 고장유형별로 동일원인이 중복해서 표기되며, 같은 원인이라도 어느 고장유형에 소속되어 정리되는가에 따라 서로 다른 RPN값을 가지게 된다. 즉, 하나의 고장원인에 대해 여러 RPN값이 부여된다. 이를 사건 발생 순서를 고려하여 그림으로 도시하면 Figure 2와 같고 하나의 공통원인에 대해 여러 개의 RPN 값이 부여되는 과정을 보여주고 있다.
이 경우 다른 고장원인과 비교할 때 이들 중 최대 RPN 값을 적용하는 것이 타당할 것인가 하는 문제에 직면하게 된다. 즉, RPN 값이 공통고장원인의 최대 RPN값보다 큰 단일 고장원인이 있다고 할 때 과연 이 단일 고장원인이 실제 위험도가 더 크다고 보는 것이 타당할 것인가 하는 문제이다. 예를 들어 2개 부품으로 구성된 병렬구조 시스템을 생각해보자. 한 부품씩 따로 고장이 났을 경우에는 시스템 기능에 별 영향을 주지 않지만 두 부품 동시에 고장난다면 시스템 기능에 중대한 영향을 미칠 수 있다. 이와 같은 상황에서 각 부품이 따로 고장 나는 상황에서 도출된 각각의 심각도를 적용하여 공통고장원인에 대해 두 개의 RPN 값을 얻었다고 하자. 그런데 하나의 고장만 유발하는 독립적인 원인에 대해 RPN을 계산하여 그 값이 공통원인의 두 RPN값보다 크다고 하여 위험도가 더 크다고 판단한다면 타당하다고 볼 수 없을 것이다. 이런 문제를 해결하기 위해서는 공통고장원인에 관련된 여러 심각도의 값을 적절하게 통합하여 하나의 값으로 나타낼 필요가 있을 것이다.
3. 수정된 FMEA
3.1 공통고장원인의 심각도 평가
앞 절에서 논의한 바와 같이 하나의 공통원인에 의해 여러 유형의 고장이 발생할 경우, 단순히 영향의 심각도가 가장 큰 고장유형을 기준으로 RPN을 산출하는 것은 문제가 있다. 현실적으로 공통고장원인의 심각도는 최소한 결과 고장들의 심각도 중 최대값 이상이 될 것이며 현실적으로는 이보다 훨씬 더 클 것이다. 베타인자모형의 예에서 살펴본바 있듯이 두 개의 동일부품이 병렬구조로 연결된 시스템일 경우 공통고장의 비율에 따라 고장확률은 10배 이상이 될 수도 있었다. 그런데 Lilleheier(2008)에 의하면 전자장비에 대한 과거 데이터에 분석 결과 베타인자모형에서 β값이 최대 0.3까지 가능하다. 이 경우 두 개의 동일부품이 병렬구조로 연결된 시스템의 고장확률은 독립적인 병렬구조에 비해 30배 이상 크게 될 것이다. MGL모형이나 알파인자모형은 부품 간 의존도가 최소한 베타인자모형 이상인 모형이므로 공통고장원인이 시스템 고장에 미치는 영향은 이보다 더 심각한 경우도 있을 것이다.
어떤 공통고장원인 CFCi이 발생하면 그에 따라 ni개 유형의 고장 F 1 , F 2 , ⋯ , F n i L 1 , L 2 , ⋯ , L n i F 1 , ⋯ , F n i p 1 , ⋯ , p n i
이 된다. 어떤 고장유형이 조합으로 발생하는가에 따라 손실 혹은 위험의 정도가 다르다고 하면 모두 2 n i - 1
Figure 3의 공통원인의 심각도는 각 조합별 발생확률을 고려하여 손실의 기대값을 취하여 다음 식으로 구한다.
단, P1=p1-p1p2-p1p3+p1p2p13, P2=p2-p1p2-p2p3+p1p2p3, P3=p3-p2p3-p1p3+p1p2p3, P12=p1p2-p1p2p3, P13=p1p3-p1p2p3, P23=p2p3-p1p2p3, P123=p1p2p3.
즉, 공통원인의 심각도는 그로 인해 유발되는 상호배반적인 고장유형 조합의 손실 혹은 위험의 크기를 발생확률을 가중치로 하여 평균한 값으로 볼 수 있다. 여기서 L1,L2,...,L123 의 값은 분석 대상 시스템의 성격이나 환경적인 여건에 따라 달라질 수 있으므로 해당 시스템 관련 전문가들의 의견을 토대로 결정하여야 한다. 예를 들어 원자력발전에 관련된 시스템을 분석 대상으로 하고 있고 고장 유형 F1과 F2의 조합이 방사능 누출을 초래한다면 이 조합에 대한 손실이나 위험의 크기 L12는 아주 크게 될 것이다.
3.2 FMEA 실시 절차
일단 공통고장원인에 대한 심각도가 하나의 값으로 통합되어 결정된다면 그에 따라 RPN 값도 하나로 결정할 수 있다. 공통고장원인에 대한 심각도를 평가하는 과정을 반영하여 수정된 FMEA의 실시 절차를 정리하면 다음과 같다.
1) 분석 대상 시스템의 모든 기능을 식별한다.
2) 기능별 고장 유형을 식별한다.
3) 고장 유형별로 고장의 영향으로 입게 될 손실 혹은 위험의 크기를 평가한다.
4) 고장유형별 원인을 식별한다.
5) 고장원인별로 고장을 유발하게 될 확률을 추정한다.
6) 고장원인별 발생도를 평가한다.
7) 단독 고장원인일 경우 그 고장원인이 고장을 유발할 확률과 고장의 영향으로 입게 될 손실 혹은 위험의 크기를 곱하여 심각도를 계산한다.
8) 공통고장원인이 있을 경우 관련된 고장유형의 상호배타적인 발생조합을 식별한다.
9) 상호배타적인 고장유형의 조합 별로 발생할 경우 입게 될 손실이나 위험의 크기를 평가한다.
10) 공통고장원인으로 인해 고장유형의 상호배타적인 조합이 발생할 확률을 계산한다.
11) 공통고장원인의 심각도를 결정한다.
12) 고장원인을 검출하기 위한 현재의 관리방법을 확인하고 검출도를 결정한다.
13) 고장원인별로 수정된 RPN을 산출한다. 이 때 수정된 RPN은 고장원인의 심각도가 어떻게 결정되었는가에 따라 1000보다 클 수도 있다.
14) RPN을 토대로 고장원인별 개선 대책을 마련하여 실시한다.
4. 예제와 논점
4.1 냉각시스템 예
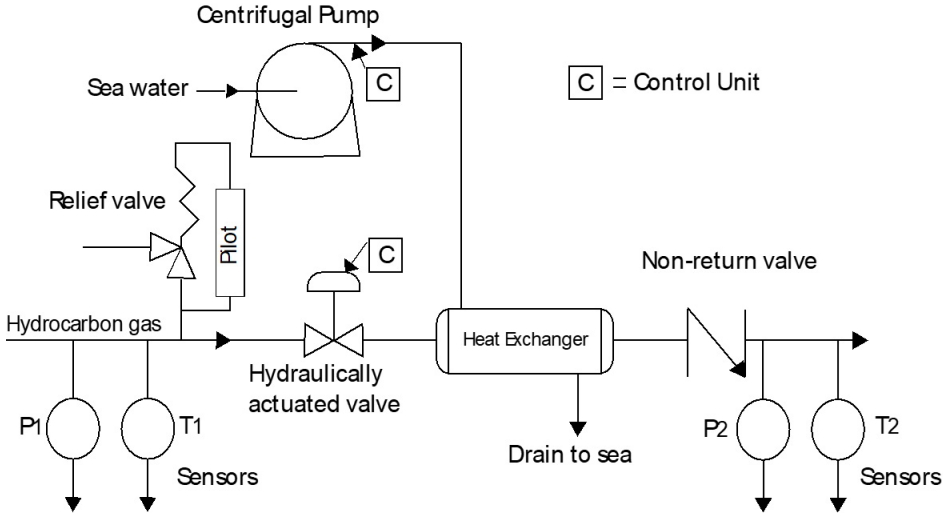
이 절에서는 예를 통하여 수정된 FMEA 실시 과정을 살펴보고 분석 결과를 비교함으로써 몇 가지 논점을 제시한다. Figure 4는 Sankar와 Prabhu(2001)가 예시한 해안 플랜트의 하위시스템인 냉각시스템의 구성을 보여주고 있다. 이 냉각시스템은 해수를 끌어올려 열교환기(heat exchanger)를 통과시키면서 냉각기능을 수행하고 다시 바다로 내보낸다.
FTA를 이용하여 냉각시스템을 분석한 결과 원심펌프(centrifugal pump)의 고장률이 가장 높아서 이 펌프에 대해 상세 FMEA를 실시하였다. 원심펌프는 해수를 퍼 올려 열교환기에 공급함으로써 탄화수소 가스를 냉각시키는 기능을 한다. 이 원심펌프의 고장 유형으로 펌프 작동불능(F1), 간헐적이고 불충분한 공급(F2), 소음 및 진동(F3), 과열 및 정지(F4), 누수(F5) 등이 식별되었다. 고장원인으로는 총 23개 단독고장원인과 7개 공통고장원인이 식별되었으나 이들 중 설명을 위해 필요한 부분만을 발췌하여 Table 1에 정리하였다. 원인 중 C4는 잘못된 회전방향, C5는 규격보다 작은 직경의 날개바퀴, C14는 베어링 마모로 인한 축의 중심 이탈, C26은 윤활부족이다.
Sankar와 Prabhu(2001)는 새로이 제시한 RPR(Risk Priority Rank)과 기존의 위험평가지표인 RPN을 함께 보여주고 전자의 유용성을 설명하고 있다. Table 1에서 C4와 C26은 단독고장원인, C14 및 C5는 공통고장원인임을 알 수 있다. Sankar와 Prabhu(2001)는 Table 1의 RPR 값인 784를 근거로 C4가 가장 중요한 원인으로 제시하고 있다. 그런데 C14의 경우 F3와 F4의 두 가지 고장을 유발할 수 있으며 어느 고장에 관계되는가에 따라 RPR 값이 각각 578, 732이다. 이 경우 둘 중 RPR이 큰 732만 고려하여 이보다 큰 RPR을 가진 C4가 더 중요하다고 판단하는 것이 타당할 것인지 의문의 여지가 있다.
고장원인의 심각도는 두 요소로 나누어 생각해볼 수 있다. 하나는 고장원인이 실제로 임무수행기간 동안 그 고장을 유발하게 될 확률이 어느 정도인가이고 또 하나는 고장이 발생했을 때 입게 될 손실이나 위험의 크기가 어느 정도 인가이다. 3절에서 이 두 가지 요소를 곱하여 고장원인의 심각도를 산출하는 것으로 제안하였다. 고장원인 C4에 의해 고장 F1이 유발될 확률이 0.5이고 실제 F1이 발생했을 때 감수해야 할 위험의 크기가 784라고 하자. 또, C14가 고장 F3와 F4를 유발할 확률이 각각 0.3, 0.5이며 단독으로 고장이 발생할 때 감수해야 할 위험의 크기가 각각 578, 732라고 하자. F3와 F4가 동시에 발생할 경우의 손실은 대부분 각각의 손실의 합보다 크게 될 것이므로 위험의 크기를 1500이라고 하자. 그러면 C4의 심각도와 수정된 RPN은
이다. 또한 C14의 심각도와 수정된 RPN은 P 1 = 0 . 3 - ( 0 . 3 ) ( 0 . 5 ) = 0 . 15 , P 2 = 0 . 5 - ( 0 . 3 ) ( 0 . 5 ) = 0 . 35 , P 12 = ( 0 . 3 ) ( 0 . 5 ) = 0 . 15
이 된다. 따라서 공통고장원인인 C14의 위험우선순위가 더 높은 것으로 판단하게 된다.
4.2 RPR과 수정된 RPN의 비교
기존의 RPN을 발생도, 검출도, 심각도의 곱으로 구할 때 1000가지의 다른 값을 가질 수 있는 것이 아니라 단지 120 개의 다른 값을 가질 수 있을 뿐으로 우선순위를 부여하는데 한계가 있다. 즉, 동일한 RPN 값을 갖는 (발생도, 검출도, 심각도)의 조합이 많이 있으므로 위험평가지표로서 우선순위부여에 사용하기에 미흡하다. 이와 같은 점을 보완하여 전문가들의 의견을 토대로 각 (발생도, 검출도, 심각도) 값의 조합에 따라 1000가지의 다른 값을 가질 수 있도록 수정된 지표가 RPR이다. Sankar와 Prabhu(2001)는 (발생도, 검출도, 심각도)의 각 값에 대응되는 유일한 RPR값을 전문가의 의견을 토대로 사전에 정해 표로 정리해두었다. 따라서 (발생도, 검출도, 심각도)의 값이 주어지면 그에 대응되는 RPR값을 표에 의해 정할 수 있다. 예를 들어 (발생도, 검출도, 심각도) = (4, 5, 6)일 경우 표를 참조하여 RPR = 492라고 정하는 것이다. 이 방법은 각 고장원인별로 관련된 고장유형이 하나로서 RPR값이 하나만 있다면 그다지 문제가 없을 것으로 보인다. 그런데 하나의 고장원인에 둘 이상의 고장유형이 관련되어 있어서 RPR이 둘 이상인 고장원인이 있다면 RPR에 의한 비교가 합리적이라고 볼 수 없을 것이다. 예로서 Table 1에서 RPR값이 732인 단독 고장원인이 있다면 RPR이 732 및 578의 두 값을 갖는 C14와 똑같은 우선순위를 갖는 것이 타당하다고 보기 어려울 것이다.
3절에서 제시된 개정된 RPN은 예시에서 살펴본 바와 같이 기존의 RPN과 RPR의 단점을 보완할 수 있는 위험평가척도이다. 그렇지만 똑같은 문제를 분석하기 위해서 더 많은 정보와 계산을 요구한다는 단점이 있다. 만약 하나의 원인에 n개 고장이 관련되어 있다면 이 원인으로 인해 각 고장이 유발될 확률 p1,p2,...,pn 을 알아야 한다. 또한 각 고장의 상호배반적인 2n-1개 조합에 대한 손실 혹은 위험의 크기를 알아야 하고 발생확률도 계산해야 한다. 만약, 공통원인이 여러 개 있으면 훨씬 더 많은 정보와 계산과정이 필요하게 된다. 더구나 여기서는 Figure 1의 (a)에서와 같이 일단 공통원인이 발생하고 나면 그 이후의 고장발생이 서로 독립적이라고 가정하고 있다. Figure 1의 (b)와 같이 공통원인이 주어지더라도 관련된 고장들이 서로 종속적으로 발생한다면 상황은 훨씬 더 복잡하게 될 것이다. 다만, 현실적으로는 냉각시스템의 예시에서 보듯이 대부분의 경우에 있어서 하나의 공통원인에 관련된 고장의 수는 그다지 많지 않다. 또한, 최근 들어 센서기술의 발전으로 고장 관련 데이터들이 많이 축적되고 있는 추세로서 필요한 정보들의 확보가능성이 높아지고 있다. 고장메커니즘에 대한 지식의 축적과 함께 컴퓨터의 연산능력 및 학습능력의 향상도 전술한 문제들을 해결하는데 도움이 될 것이다.
일단 우선순위가 높은 원인이 공통고장원인인 것으로 결정되면 기능적, 공간적, 인간적, 환경적 요인 등 공통원인으로 묶어주는 결합요인(coupling factor)들 중 가장 중요한 요인이 무엇인지 조사하여 조치 방향을 설정하는 것이 좋을 것이다.
5. 결 론
FMEA에서 공통원인고장이 있을 경우 고장원인에 대한 개정된 위험우선순위 평가지표를 제안하였다. 개정된 RPN은 기존의 RPN 산출방식을 보완하여 고장원인의 발생도와 검출도는 그대로 사용하되 심각도는 원인이 고장을 유발하게 될 확률과 여러 고장이 한꺼번에 발생할 경우의 위험 증가를 함께 고려하여 산출하였다. 그 결과 개정된 RPN은 기존의 RPN과 달리 최대값이 1000으로 제한되지 않고 위험의 크기에 따라 더 큰 값을 가질 수 있도록 허용하였다.
개정된 RPN은 기존 RPN이 취급할 수 없는 공통고장원인에 대한 위험을 보다 합리적이고 객관적으로 처리할 수 있다는 장점이 있다. 그동안 기존 RPN의 단점을 보완하기 위한 연구는 많이 이루어졌으나 공통고장원인에 대한 위험평가지표를 제시한 연구는 거의 없다. 조사된 바로는 한두 편 정도만이 공통고장원인에 대해 언급하고 있으나 위험평가에 있어서 다른 고장원인과 공정한 비교를 하고 있다고 보기 어렵다. 이 연구에서는 한 걸음 더 나아가 공통고장원인에 대한 체계적인 위험평가절차와 개정된 RPN을 도입함으로써 공통고장원인에 대한 위험평가의 공정성과 객관성을 확보할 수 있도록하였다.
개정된 RPN은 FMEA에서 기존의 위험평가지표들이 가진 몇 가지 단점들을 보완하였지만 사용을 위해 많은 정보와 연산이 필요하다는 단점이 있다. 또한 공통원인이 발생된 이후 관련 고장들의 발생과정이 독립적으로 진행되는 것으로 가정하였는데 현실적으로는 그렇지 못한 상황도 흔하다. 이와 같은 한계점들은 향후의 연구에서 해결방안이 나올 것으로 기대한다.