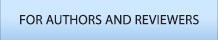1. 서 론
자원제약이 존재하는 프로젝트 일정에서 선행활동 품질수준이 후행활동의 시간과 비용에 미치는 영향에 대한 문제는 현대 시대의 거의 모든 산업분야에서 수행하고 있는 프로젝트의 활동들에 많은 영향을 주고 있다(Yoon and Jo, 2022). 따라서 본 연구는 프로젝트 활동들의 일정문제에 대하여 분석하고, 의사결정에 반영하는 알고리즘을 제공하고자 한다.
1.1 문제의 배경
일반적으로 프로젝트 활동은 “기획 → 분석 → 설계 → 개발 → 통합 → 검수 → 납품” 등으로 진행하는데 있어서, 모든 활동들의 시간과 비용이 정해진 상태에서 진행되고 있다(Ahn and Min, 2008). 그러나, 본 연구에서 프로젝트 활동의 시간과 비용은 선행활동의 결과에 따라서 후행활동 들에게 영향을 미친다는 것이다. 예를 들어, “기획활동” 보다 나중에 수행되는 “분석활동”은 선행활동인 “기획활동”의 결과에 따라 “분석활동”에 영향이 있다고 판단할 수 있다. 이러한 프로젝트 일정문제에 대한 연구는 <Figure 1>과 같이 선행활동의 수행 결과에 따라 후행활동의 시간과 비용이 달라진다. 프로젝트 활동에서 후행활동의 시간과 비용을 감소시키려면, 선행활동의 완성도를 높여야 하므로 시간과 비용이 증가할 것이고, 그의 역도 성립될 것이다. 프로젝트 일정에 대한 대부분의 연구들은 이미 정해진 시간과 비용만이 적용되고 있으며, 정해진 시간과 비용을 선택적으로 변경하여 목적함수 값을 찾는데 그 목적이 있었다. 본 연구에서는 Kim(2016) “자원제약을 고려한 프로젝트 일정문제에서 품질과 시간, 비용간의 트레이드오프 문제”의 품질지수 선정에 대한 추가적인 연구에 목적이 있다. 따라서, 선행활동의 품질수준이 자신 및 후행활동의 시간과 비용에 영향을 미치는 연구는 매우 미흡하여, 이를 다루고자 하였다.
이를 위해, 프로젝트 활동의 품질지수(Quality Index, QI)를 제안하였다. QI는 활동 i와 모드 m, 품질수준 q가 존재한다고 가정하면, QI(i,m,q)이다. 여기서, QI가 1.0보다 크면 후행활동의 시간과 비용이 감소됨을 의미하고, 1.0이면 변동 없음을 1.0보다 작으면 시간과 비용이 증가함을 의미한다. 활동의 품질수준(Quality Level, q)은 고품질, 보통품질, 저품질로 구분되며, 결정되는 시간(Applied Time, at)과 비용(Applied Cost, ac)은 사전에 알려진 시간(Make Time, MT), 비용(Make Cost, MC) 에 QI를 적용하여 결정되는 것이다.
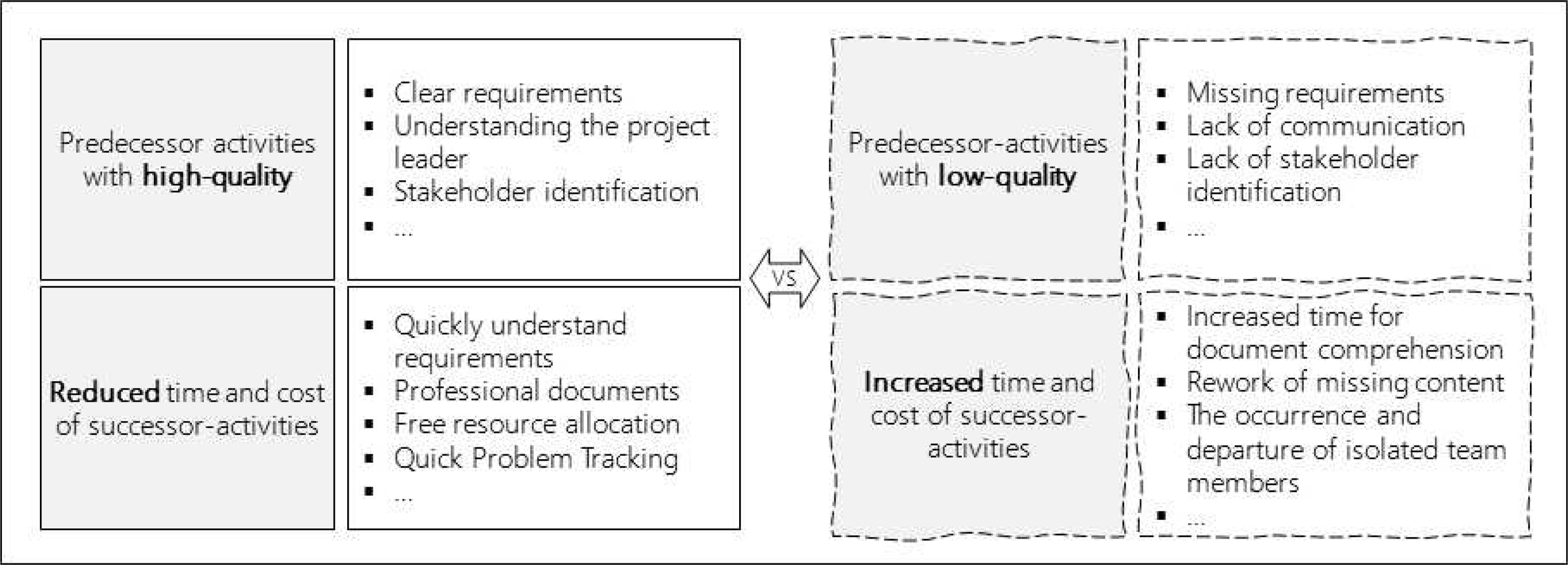
<Figure 4>에서 사전에 알려진 선행활동 [MT, MC]=[12, 1200]이 고품질(QI=1.1)로 수행될 경우 [at, ac]=[13.2, 1320]으로 증가된다. 이는 자신의 활동에 선행활동이 존재하지 않으므로 자신의 [MT, MC]에 QI를 곱하여 결정된다. 그리고, 후행활동의 [MT, MC]=[9, 900]이라면, at=9÷1.1=8.2, ac=900÷1.1=818.2로 수행된다. 여기서, 선행활동의 QI는 q에 의해 적용된다. 프로젝트의 모든 활동에 고품질의 QI를 적용하거나, 저품질의 QI를 적용하여, 정해진 종료시간 안에서 프로젝트를 수행해야 한다면, 모든 활동들을 대입하여 적용해야 최적해(Optimal-solution)를 찾을 수 있을 것이다.
이러한 프로젝트 활동은 “선행활동의 품질수준에 따라서 선행활동과 후행활동은 시간과 비용의 Trade Offs 문제”가 성립되며, 선행활동의 QI가 높은 수준으로 진행되었다면, 후행활동의 시간과 비용은 감소하고, 반대로 선행활동의 QI가 낮은 수준으로 진행되었다면, 후행활동의 시간과 비용은 증가한다는 특징이 있다. 본 연구에서는 높은 QI라 하더라도 활동들의 특성에 따라 1.1~1.3사이의 QI를 달리하여 수행된다는 가정에서 문제를 해결하고자 하였고, 보통수준의 QI는 0.9~1.1 사이로, 낮은 수준의 QI는 0.7~0.9사이로 구성하여 프로젝트가 수행되도록 하였다. 그리고, 사전에 알려진 QI는 다음과 같이 표현할 수 있다. x ¯ i ¯ , m ¯ , q ¯
또한, 현재 진행활동의 선행활동이 다수 존재하는 경우 QI의 산출방식은 “산술평균”과 “기하평균”으로 산출할 수 있다.
(1) 가중 산술평균일 경우: QI=1.3w1+1.1w2+0.9w3
(2) 가중 기하평균일 경우: Q I = 1.3 1 w + 1.1 2 w + 0.9 3 w
본 연구에서는 데이터에 대한 산정 문제이므로 산술평균(w i = 1 n
1.2 품질지수 산정방법
프로젝트 활동들이 <Table 1>과 같이 진행된다면, 프로젝트 활동 중 개발활동(a4)은 선행 분석활동(a2;)과 설계활동(a3)이 종료되어야만 시작할 수 있다. 예를 들어, 사전에 정해진 프로젝트 종료시간(Due Time, DT)는 [95]이고, 모든 활동의 m은 [1]로 설정하고, 활동들의 QI을 고품질로 적용한다면, 프로젝트 총 수행시간(Total Time, tt)과 수행비용(Total Cost, tc)은 [99, 9589]로 계산할 수 있다. 반대로 모든 활동들의 QI을 저품질으로 적용한다면, [tt, tc]=[93.3, 9972.6]으로 계산할 수 있다. 여기서, 고품질 tt=[99]와 저품질 tt=[93.3]으로, 저품질일 경우 프로젝트를 조기에 종료할 수 있을 것이다. 또한, 총 수행비용은 고품질 [9589]와 저품질[9972.6]으로, 고품질일 경우 수행비용은 더 저렴하게 수행할 수 있을 것이다. 따라서, min(tt)가 목적일 경우에는 저품질로 프로젝트를 수행하여야 하고, min(tc)가 목적인 경우 고품질로 수행되어야 한다는 의사결정이 될 수 있을 것이다.
본 연구에서는 총 수행비용 최소화를 목적함수로 하는 해를 탐색하고자 하는 것이므로 고품질 프로젝트 수행이어야 하지만 고품질의 경우 종료시간이 [4]만큼 지연되었으므로, 종료시간 단위마다 패널티 비용(Penalty Cost,PC)를 부과 한다면 의사결정변수는 저품질로 프로젝트가 수행되는 것을 허용할 수 있을 것이다. 이러한 프로젝트 일정은 <Table 1> 바탕으로 tt와 tc를 <Table 2>와 같이 계산될 수 있다.
이러한, 프로젝트 활동들의 품질지수 산정은 다음과 같다.
(1) 선행활동이 존재하지 않을 경우: at(i) = MT(i) × QI(i),
ac(i) = MC(i) × QI(i)
(2) 선행활동이 존재할 경우: at(i) = MT(i) ÷ QI(pre Act),
ac(i) = MC(i) ÷ QI(pre Act)
※ pre Act(직접적인 선행활동)
1.3 문제의 차별성
“자원이 제약되고, 활동별로 복수의 모드가 존재하는 프로젝트 일정문제”에서 기존 연구들은 ac와 ac가 선정되는 m에 의해서 결정되었다. 즉, ai가 aj의 선행활동인 경우, ai의 at와 ac는 aj의 at와 ac가 서로 독립적으로 진행된다는 것이다. DT와 선정된 비용 내에서 수행한다는 조건이 존재하고, 각 활동의 QI가 다르게 적용된다면, 모든 프로젝트 활동들에 QI를 대입하여 문제를 해결할 필요가 있을 것이다. 따라서, 본 연구에서 프로젝트 활동의 at와 ac는 선정된 m이 존재하고, 선정된 m에 대한 QI가 있으며, 현재활동의 at와 ac는 선행활동의 q에 의해 결정된다는 것이다. 즉, ai가 aj의 선행활동인 경우, ai의 QI에 따라 aj의 at와 ac이 결정되는 Trade-offs 문제로써 기존 연구들과 차별점이 있다.
2. 이론적 고찰
본 연구는 자원제약을 고려한 활동별 복수모드와 품질지수가 존재하는 프로젝트 일정문제에서 선행활동 품질수준이 후행활동 시간, 비용에 미치는 영향에 대한 일반화한 알고리즘 문제이다.
Icmeli-Tukel and Walter(1997)는 프로젝트 품질을 최대화할 때 얻어지는 총 소요시간이 최소화되고, 프로젝트 가치가 시간과 비용 측면에서 기존의 일정계획보다 효과적인 것을 설명하였다. Vikram et al.(2009)은 선택 가능한 모드가 복수인 경우, 주어진 자원들이 사용되는 기술수준에 품질차이가 존재하여 자원들에 대한 훈련이 필요함을 설명하였다. 이러한, 프로젝트 일정문제의 연구에서 활동에 대한 at와 ac은 선택 가능한 m에 의해서 결정되었다. 이것은 ai가 aj의 선행활동인 경우, ai의 at와 ac, 그리고 aj의 at와 ac가 서로 독립적으로 수행된다.
본 연구에서는 an의 at와 ac는 선택 가능한 m과 q에 의해서 결정된다는 것이다. 즉, ai가 aj의 선행활동인 경우, ai의 q에 의해 aj의 at와 ac이 결정된다는 것이다. 따라서, aj의 at와 ac는 ai의 q에 독립적이지 않고, 매개로써 존재하므로 독립적인 경우를 포함하고 있다.
2.1 시간-비용 트레이드-오프 문제
프로젝트 활동의 시간과 비용의 Trade-offs 문제는 활동에 적용되는 추가 비용에 의해 감소되고, 활동들의 선행과 후행에 대한 관계는 고려되지만 요구되는 자원제약은 고려하지 않는다(Ahn and Erenguc, 1998). 그리고, 활동들간 시간과 비용 Trade-offs 문제의 기본적인 개념은 특정한 활동의 일정문제가 아니라 실행 가능한 모든 활동들의 일정에 대한 문제들이다(Kelley, 1961). 프로젝트 일정문제에서 시간과 비용의 최소화 문제를 다룰 수 있는 동적(Dynamic) 프로그램 알고리즘과 불연속적인 시간과 비용 Trade-offs 문제를 위한 분기한정기법(Branch and Bound Method)들을 사용하여, 시간과 비용의 최소화 문제를 해결할 수 있다(Robinson, 1975; Sprecher, 2002).
따라서, 프로젝트 시간이 지연될 위험이 존재하는 경우, 더 많은 비용 혹은 자원을 증가시켜 시간을 단축시킬 수 있다. 이러한 프로젝트 시간과 비용 문제에서는 최적의 시간과 비용이 존재한다(Tormos and Lova, 2003). 이러한, 단일목적함수는 시간과 비용의 최소화 또는 최대화를 의미하며, 연산의 난이도는 선형계획법보다 수월한 문제라 할 수 있다(Carolin and Helber, 2015). 본 연구에서는 프로젝트 활동들의 선ㆍ후행관계에서 품질수준을 적용한 시간과 비용의 최소화 문제를 다루고자 하였다.
2.2 단일모드에서 자원제약을 고려한 프로젝트 일정문제
단일모드에서 자원제약을 고려한 프로젝트 일정문제는 사전에 알려진 자원과 목적함수의 완료시간 최소화에 대한 문제이다. 이러한 일정문제에 대한 일반적인 가정은 활동기간, 비선점(Non-preemptive)활동, 자원제약, 활동간의 선ㆍ후행 관계를 포함한다(Ahn and Min, 2008).
이러한 프로젝트 일정에 대한 문제는 각각의 활동들의 가장 빠른 시작시간을 선정하고, 이를 만족하는 해가 존재하면 활동들의 시작시간 배정은 종료된다. 만약, 그렇지 않으면 활동의 시작시간을 한 단위씩 뒤로 이동하며 실행 가능한 해를 찾을 때까지 반복한다. 이러한 배정과정을 통하여 최적해(Optimal-solution)를 찾는 것이다. 여기에서 목적함수는 비용 최소화 문제로 자원충돌(Resource-conflict)이 발생할 때마다 어떠한 활동을 지연할 것인지 혹은 어떠한 활동을 우선 진행할 것인지에 따라서 활동들의 시작시간은 달라진다.
※ tc(프로젝트 총비용), ac(적용된 각 활동들의 비용), PC(프로젝트 패널티 비용), pt(프로젝트 종료시간), DT(사전에 알려진 프로젝트 종료시간)
따라서, 활동들에 대한 배정 우선순위 결정에 의해서 시작시간이 결정되는 것으로 활동의 수가 n개일 경우 우선순위를 결정해야 한다면 n!의 문제로 매우 큰 경우의 수가 발생하게 되는 것이다(Taha, 2016).
2.3 복수모드에서 자원제약을 고려한 프로젝트 일정문제
프로젝트 일정문제에서 각 활동들의 수행을 위해 허용 가능한 모드에 의해 지정할 수 있다. 각 모드는 특정한 자원의 유형에 따라 처리시간과 비용으로 구성되어 있는 특징이 있다. 따라서, 다양한 목적함수를 가지고 있고, 일정하거나 변화되는 자원의 수준을 가지는 문제에 활용되고 있다(Madjid et al., 2014). 또한, 복수 모드를 가지는 프로젝트 일정문제에서는 어떠한 모드를 선택하느냐에 따라서 일정이 변화되는 특징을 알 수 있다(Masanori and Suzuki, 2010).
목적함수는 단일모드를 적용한 프로젝트 일정문제와 동일하며, 의사결정 변수는 각 활동의 모드와 시작시간이 되고, 시간과 비용, 종료시기는 종속적으로 결정된다. 이러한 복수모드의 연산 난이도는 n!개와 조합된 모드 경우의 수 mn을 곱한 것과 같다(Elham et al., 2014). 이러한, NP-Hard Class의 문제는 다항식으로 표현할 수 있는지 여부가 알려져 있지 않는 매우 어려운 문제라 할 수 있다(Yim, 2011).
2.4 기타 주요연구 내용
입자 군집 최적화 방법을 활용하여 다층 구조 시스템이 중복되는 최적 할당 방법에서, 신뢰도가 높은 부품을 사용하거나, 비슷한 기능의 부품을 사용함으로써 향상시킬 수 있다. 비슷한 기능을 가진 부품은 다양하게 존재하며, 어떠한 부품을 적용하느냐에 따라 시스템의 기능성, 신뢰성, 시간, 비용, 크기 등이 달라질 수 있다(Chung, 2019).
좋은 품질을 확보하기 위하여 초기 단계에서 설계에 대한 적합성을 검토하여 프로젝트 일정 및 제조공정에서 발생 가능한 품질저하 등 고장, 결함 및 불량에 대한 사전 검토와 대책으로 대비하는 것이 매우 중요하다(Kim et al., 2007). 제품의 초기 설계 단계에서부터 생산 단계에 이르기까지 의도한 대로 기능을 발휘하는가를 평가하고, 만족하지 못할 때는 개선 활동을 통해 설계 단계로 개선 사항이 전달될 수 있도록 수행하는 신뢰성 및 효율성 평가 활동이 필요하다(Cho et al., 2022).
자원제약을 고려한 프로젝트 일정문제를 다루기 위해 참고한 주요연구는 <Table 3>의 정리내용과 같다.
3. 수학적 수식(Mathematical Formulation)
3.1 주요 가정
본 연구에서의 주요 가정은 10가지로 설정하였다. (1) 프로젝트의 활동과 활동에 대한 선ㆍ후 관계는 확정적이다. (2) 프로젝트에서 활동들은 선택 가능한 복수의 모드가 존재한다. (3) 활동별 모드 내에 품질수준이 존재한다. (4) 활동별(모드, 품질수준) 조합에 따라 활동의 수행 시간과 비용이 결정된다. (5) 위의 시간과 비용은 해당 활동의 선행활동들의 품질수준에 따라 조정된다. (6) 활동별 모드에 따라 필요한 자원의 종류 및 수량은 확정적이다. (7) 프로젝트의 모든 시간에 걸처 자원의 종류별 가용량은 확정적이다. (8) 프로젝트 일정에 의한 자원의 요구량은 가용량을 초과할 수 없다. (9) 한번 시작한 활동은 다른 활동에 의해 중단될 수 없다(Non-preemptive). (10) 프로젝트는 종료시간이 존재한다. 종료시간 보다 일정이 지연되면, 지연된 시간에 따른 지체보상금이 발생하는 것이다.
3.2 문제의 수식화
본 연구에서 수학적 수식은 다음과 같다.
Minimization:
Subject to:
여기서, (1)은 목적함수를 의미한다. 목적함수는 [활동 비용의 합 + 프로젝트 지체보상금]으로 계산한다. 프로젝트 지체보상금 pc는 첫째, 활동들 중에서 종료시간이 가장 큰 종료시간 pt와 사전에 알려진 프로젝트 종료시간 DT를 감산한 기간 중 큰 값을 선정한다. 둘째, pt와 DT를 감산한 큰 값을 사전에 알려진 시간단위 지체보상금PC로 곱한 값이다. 여기서, 프로젝트 지체보상금 pc =PC × max[pt(i + 1)- DT,0]로 표현할 수 있고, 활동들 중 종료시간이 가장 큰 종료시간은 pt = max[at(i)]로 표현할 수 있다. (2)는 각 활동별로 모드의 품질수준은 하나만 선택한다. 여기서, M(i)는 활동 i가 모드 m으로 진행될 때 품질수준의 집합이다. (3)은 활동 i에 적용되는 시간의 품질지수 qit(i)는 활동 i의 선행활동들 pre Act(i)의 선정된 시간에 대한 품질지수 가중평균이다. (4)는 활동 i에 적용되는 비용의 품질지수 qic(i)는 활동 i의 선행활동들 pre Act(i)의 선정된 비용에 대한 품질지수 가중평균이다. (5)는 활동 i의 기준 시간 bt(i)와 비용 bc(i)는 이미 알려진 자신의 시간 MT(i)와 비용 MC(i)에 선행활동 품질지수 가중평균 qit(i)와 qic(i)를 곱한 값이다. (6)은 활동 i에 적용된 기간 at(i)와 비용 ac(i)는 기준 시간 bt(i)와 비용 bc(i)에 이미 알려진 자신의 품질지수 QI(i)로 나눈 값이다. (7)은 st(i)는 활동 i의 배정되는 시작시간이다. 활동 j가 활동 i의 후행활동이면, 활동 j의 시작시간은 활동 i의 종료시간보다 앞설 수 없다. (8)은 st는 시점 t에 진행 중인 활동의 집합을 의미한다. 이러한 표기는 개념적 서술로써, 일정이 확정된 이후에 파악되는 집합이다. 그렇지 않으면 표기가 너무 방대해진다. LP나 IP로 문제를 푸는 경우, 명시적 표현이 필수지만, 다른 알고리즘을 사용하는 경우 개념적 서술로도 충분하다. rink는 활동 i가 모드 m으로 진행될 때 요구하는 자원 k의 수량을, bk는 자원 k의 가용량을 의미한다. 위 식은 일정에서 요구하는 자원의 수량이 매 시점별로 가용량을 초과할 수 없음을 나타낸다.
4. 알고리즘의 약술 및 실험 결과
본 연구에서의 사용한 최적화 알고리즘은 Kim(2016)에서 제시한 최적화 기법의 탐색기법과 효율성 제고 방식을 사용하였다. 문제의 크기가 증가하고 그로 인한 최적해를 구하는 시간이 현실적으로 허용할 수 없는 범위를 벗어나는 경우 최적해가 아니더라도 최적해에 가까운 해를 찾기 위해 메타-휴리스틱 절차(Meta-heuristic Procedure)를 사용하였다.
4.1 최적화 기법
최적화 기법은 모든 제약조건을 충족하는 실행가능해(Feasible-solution)가 하나라도 존재한다면, 반드시 최적 실행가능해(Optimal Feasible Solution)를 찾아내는 기법이다. 이러한 최적화 기법은 NP-Hard Class의 경우, 문제가 커지면 최적해를 찾는데 소요되는 시간이 급증하여, 현실적인 시간 내에 최적해를 제시하는 것이 불가능하다.
이러한 최적화 기법을 본 연구에서 제시하는 이유는 작은 크기의 문제일 경우 최적해를 찾는데 사용하고, 제시할 메타-휴리스틱 기법에서 제시하는 해(Solution)가 얼마나 최적에 근접하는지를 검증하고자 하였으며, 본 연구에서 사용되는 최적화 기법은 Kim(2016)의 전체 열거법(Total-enumeration)을 기반으로 하였다. 전체 열거법은 가능한 모든 해를 순서적으로 나열하면서 각 활동의 가능 여부(Feasibility)를 탐색하고, 실행 가능한 해 중에서 목적함수 결과 값이 가장 좋은 것을 최적해 값(Optimal-solution Value)으로 하였다.
4.1.1 해(Solution) 영역
본 연구에서 문제의 해(Solution)는 각 활동별 모드와 품질수준 그리고 시작시간으로 구성된다. 문제의 수식에서 xii,m,q는 0 또는 1의 값을 갖는데, x i ¯ , m ¯ , q ¯ = 1 i ¯ m ¯ q ¯
4.1.2 전체 열거법(Total Enumeration)과 경우의 수
전체 열거법이(Total Enumeration)란 가능한 모든 해를 체계적으로 나열하면서 각 해의 실행 여부(Feasibility)를 탐색하고 실행 가능한 해(Feasible Solution)이면 그 해의 목적함수 값을 탐색한다. 가능한 해를 모두 탐색한 후 실행 가능한 해가 하나도 없으면 실행 가능한 해가 하나도 없다고 보고한다. 하나라도 있으면 실행 가능한 해 중 목적함수 값이 가장 좋은 것을 최적해로 하고, 그 목적함수 값을 최적해 값(Optimal Feasible Solution Value)으로 한다(Sprecher, 2002).
본 연구의 해 영역에서 활동별 선정 모드와 품질수준은 유한한 경우의 수를 갖는다. 예를 들어, ai의 선택 가능한 m = 3이고 각 모드 별로 선택 가능한 q = 4라면, ai의 m과 q의 가능한 조합은 총 12개가 된다. 프로젝트를 구성하는 활동의 수가 N이므로, 활동 별 가능한 m과 q의 조합이 총 12개씩이라면 프로젝트 전체 활동의 조합 수는 N12가 된다. 즉, N이 커질수록 N12의 값은 급증하지만, 이 수는 여전히 유한한 값이다.
4.1.3 최적화 기법 알고리즘
전체 가능한 모든 해를 체계적으로 나열하기 위해 Sprecher(2002)의 선행나무 개념을 바탕으로 적용하였다. 따라서, 모든 해는 활동의 배정순서에 따라 표현한다. 이러한 활동은 오름차순으로 정렬한다. 여기서 aimq는 활동, 그 활동에 배정된 모드와 품질수준을 의미한다. 활동들의 st조합중에서 활동 간의 선행관계를 위배하는 순서조합은 제거되어야 한다. 예를 들어 ai는 aj의 선행활동이라 하자. aj의 배정순서가 ai의 배정순서보다 앞서 있다면 그 순서조합은 실행가능한 해를 만들 수 없다.
최적화 알고리즘에서 l은 활동의 배정순서를 말한다. 예를 들어 l = 3이란 이미 두 활동이 배정(시작시기, 모드와 품질수준 배정)되었고, 세 번째로 활동이 배정되는 단계임을 의미한다. cAs란 이미 배정된 활동들의 집합, nAs란 아직 배정되지 않은 활동들의 집합을 나타낸다. 알고리즘에서 배정 고려중인 활동은 cActi로 배정되었다. 제거되는 활동은 oActi로 표현했다. cAs, nAs, cActi와 oActi는 l이 변경될 때마다 값은 변경된다. 활동 cActi는 (1) stcActi는 이전 l에 배정된 활동의 시작시기보다 앞설 수 없다. (2) stcActi는 자신 선행활동들의 종료 시점보다 앞설 수 없다. (3) cActi가 [stcActi, etcActi]에 배정되어도 자원이 부족하지 않는 조건을 모두 충족시키는 가장 빠른 시점에 배정한다. 최적화 알고리즘은 Kim(2016)과 Ryu(2017)에서와 같이 다음의 과정을 수행한다.
Step 0. 초기화
Step 1. Forward l의 값을 1단위 증가시킨다. 현재 l에 i를 배정하고, i의 첫 번째 m, q 조합을 배정하고, Step 5로 이동한다.
Step 2. 모드/품질수준 증가
현재 l에 배정된 m, q이 배정된 활동의 마지막 m, q이 아니면, 다음 번 m, q 조합을 배정하고 Step 5로 이동한다. 그렇지 않으면 Step 4로 이동한다,
Step 3. Forward에서 배정할 활동 선정
nAs에 속한 활동 중 인덱스가 가장 낮은 활동을 cActi로 한다. Step 1로 이동한다.
Step 4. Backtracking
현재 l에 배정된 활동을 oActi라 하자. 다음 l을 1단위 감소 시킨다. 여기서, l = 0이면 종료하고, 그렇지 않으면 Step 6으로 이동한다.
Step 5. Solution 완성 여부 확인
l = N이면 Solution은 완성되었다. Step 2로 이동한다. 그렇지 않으면 Step 3으로 이동한다.
Step 6. 선행 관계를 고려한 다음 번 배정 활동 선정
(1) nAs에 oActi보다 큰 인덱스의 활동이 존재하면, 그 활동집합에서 인덱스가 가장작은 활동들을 cActi이다. 만약 cActi의 선행활동이 nAs에 포함되어 있으면, oActi = cActi로 치환한다. 그리고, Step 6으로 이동한다.
(2) (1)에 해당되지 않으면 Step 2로 이동한다.
본 연구에서 적용한 최적화 기법의 전체 열거법은 소요되는 연산시간을 단축하기 위해 Sprecher(2002)가 소개한 5개의 규칙 중 중복 제거에 관한 규칙만 적용하었다.
4.2 이웃탐색 휴리스틱 기법
자원제약을 고려한 프로젝트 일정문제는 최근 복수의 모드를 지닌 문제(Resource Constrained Project Scheduling Problem with Multi-Modes, RCPSPMM)가 가장 많이 연구되고 있다. 앞서 서술한 Ryu(2017)의 문제도 이 부류에 속한다. 이 문제의 해는 각 활동별 선정 모드와 시작시기로 구성된다. 이런한 문제들은 전형적인 NP-Hard Class 문제로써 최적해를 구하는 데 소요되는 연산시간이 급증하므로, 메타-휴리스틱 기법에 대한 다양한 연구가 진행되어 왔다(Ahn and Erenguc, 1998). 메타-휴리스틱 알고리즘은 오래전부터 개발되어 왔으며, 현대에는 선형계획법(Linear Programming, LP) 문제를 대용량 컴퓨터로 연산하고 있다(Debels and Vanhoucke, 2007). 본 연구에서 RCPSPMM과 차별되는 점은 선행활동의 품질수준이 후행활동의 수행기간이나 비용에 영향을 끼친다는 것이다. 그러므로 이웃탐색 휴리스틱 기법은 각 활동의 품질수준에 초점을 맞추었다.
4.2.1 이웃탐색 알고리즘
이웃탐색 알고리즘(Neighborhood-search Algorithm)은 반복적으로 연산되는 과정을 임의로 선정한 가능해로부터 시작하여 이웃에 있는 더 좋은 해가 있는 곳으로 이동을 시도한다. 즉, 주어진 해보다 더 좋은 해를 찾기 위해서 이웃에 있는 모든 가능해를 탐색하고, 더 이상 개선이 불가능할 경우 종료한다(Hillier and Lieberman, 2015). 본 연구에서 제안하는 이웃탐색 알고리즘은 다단계 알고리즘(Multiple Pass Algorithm)으로써 초기 실행가능 해 생성과 이웃탐색 알고리즘을 통한 개선의 과정을 주어진 시간 동안 반복한다.
Step 1. 초기해 생성
연산시간이 미리 설정한 시간을 경과했으면, 지금까지 발견된 가장 좋은 해를 휴리스틱의 해로 제시하고, 종료한다. 그렇지 않으면, 실행가능해(초기해)를 생성하고 Step 2로 이동한다.
Step 2. 이웃탐색
(1) 각 ai의 m, q 조합 변경 테스트
ai의 m, q 조합 변경시 목적함수 값이 개선되면 해를 업데이트 한다.
(2) 이웃탐색
각 ai의 st를 앞으로 전진시킬 수 있다면 해를 변경한다.
(3) 이웃탐색 반복 여부 테스트
(1)과 (2)의 수행에서 해가 변경되었다. Step 2로 이동한다. 그렇지 않으면 Step 1로 이동한다.
4.2.2 초기 실행가능해 생성
본 연구에서 문제의 해는 각 ai의 m, q 그리고 st로 구성한다. 이러한 구성은 aimq의 부분해와 st(i) 부분해로 구분할 수 있다. 초기 실행가능해에서 aimq의 부분해를 결정하는 방법은 다수 존재한다. 프로젝트 마감일이 촉박하고 지체 보상금이 클 경우 활동별로 수행기간이 가장 짧은 모드와 높은 품질수준을 배정할 수 있고, 프로젝트의 수행기간보다 비용이 문제인 경우 활동별로 가장 저렴한 모드와 품질수준을 배정할 수 있다. 프로젝트 자원제약이 존재하는 문제인 경우에는 활동별로 자원 요구량이 가장 작은 모드를 배정하고 품질수준은 임의로 배정할 수 있다. 프로젝트에서 가장 중요한 요소가 시간인지, 비용인지 아니면 자원인지가 불분명할 때는 활동별 모드와 품질수준을 임의로 설정하는 것도 하나의 방법이다.
Phase 1. 최초의 초기 실행가능해 생성
프로젝트 활동들의 특성 중 하나는 어떤 요소가 가장 중요한 것인지 불분명하다. 따라서, 이웃탐색 알고리즘의 초기해는 프로젝트를 수행하는 모든 aN의 m, q을 무작위로 설정하였다.
Phase 2. m, q의 무작위 배정
m, q은 무작위(Random)로 배정하였다. 여기서, M(i)란 활동 i의 선정 가능한 모드의 수이고, Q(i,m)은 활동 i의 모드로 m이 선정될 때 선정 가능한 품질수준의 수를 나타낸다. m = [z(random × 10000)mod M(i)] + 1, q = [z(random × 10000)mod Q(i,m)] + 1 m이나 q는 무작위로 생성된 큰 정수 값을 M(i), Q(i,m)으로 나누었을 때의 “나머지+1”로 배정하였다. random은 0~1 사이의 실수인 난수이다. 큰 값으로 만들기 위해 난수에 10000을 곱했다. z(A)는 A를 정수로 변환하는 것이다. B modC는 B를 C로 나누었을 때의 나머지를 의미한다.
Phase 3. ai의 시작시기 배정
ai에 대한 시작시기를 배정하기 위해서 “어떤 활동 순으로 배정할 것인가?”를 먼저 정한다. 예를 들어, aA, aB, aC가 시점 0에 배정될 수 있고 각 활동을 수행하기 위해서는 특정 자원(R)이 2단위씩 매 기간 필요하다고 하자. 만약 프로젝트에서 사용 가능한 자원이 기간 1에 4단위만 있다면, 활동들은 시점 0에 동시에 시작하는 것은 불가능하다. 그러므로 활동들 중 하나는 시점 0이 아닌 이후 시점으로 시작시기가 되어야 한다. 또한, 어떤 활동의 시작시기를 연기해야 하는가에 대한 역은 “어떤 활동을 먼저 배정할 것인가?”이다. 프로젝트에 가능한 활동들의 배정순서는 다수 존재한다. 따라서, 초기 실행가능해에 적용될 활동들의 배정순서는 난수로 생성하였다.
Phase 4. ai의 배정순서는 무작위로 생성
Step 0. 초기화
cAs = (), nAs = (0,1,2,...,N)
Step 1. 활동들의 배정순서 적용
cAs에 포함된 순서를 활동들의 배정순서로 한다. 그리고, 종료한다.
그렇지 않으면,
(1) nAs생성
nAs에 포함된 활동들 중 선행활동들이 모두 cActi에 포함되어 있는 활동들로 cAs를 생성한다.
(2) cAs에 포함된 활동 둘 하나를 임의로 선택한다. 선택된 활동이 ai라 한다면, cAs = cAs + ai, nAs = nAs - ai를 적용하고, Step 1로 이동한다.
여기서, 선정될 활동들의 순서는 Rank = [z(random × 10000)mod |cAs|] + 1로 선정한다. Rank는 cAs의 활동들을 오름차순으로 정렬할 때의 순위를 의미하고, |cAs|는 cAs에 포함된 활동들의 수를 의미한다. 예를 들어, cAs = (4, 5, 6)이라 하면, |cAs| = 3이고, a4의 Rank = 1이다. 만약, Rank = 2이면, 현재 단계에서 a5를 배정순서에 포함한다. Step 1이 반복될 때마다 하나의 활동이 배정순서에 포함되므로, Step 1이 N번 반복되면 활동의 배정순서는 완성된다.
Phase 5. ai의 배정순서에 따른 활동의 시작시기 배정
aimq가 결정되었고, 배정순서 또한 결정되었으므로 실행 가능한 초기해를 생성시킬 수 있다. 배정순서에 따른 활동별 시작시기 배정은 최적화 기법에서 Step 1 중 활동 cActi의 시작시기 배정과 동일하다.
Phase 6. 이웃탐색 실행 순서 이후의 초기 실행가능해 생성
4.2.1 이웃탐색 알고리즘의 Step 2에서 더 이상 개선이 이루어지지 않는다면, 현재의 해 영역에서 다른 해 영역으로 이동하여 해의 개선을 시도하여야 한다. 이를 위한 초기 실행가능해는 직전 이웃탐색의 결과를 무시하고 완전 새로운 해를 생성하거나 아니면, 직전 이웃탐색에서 구한 해를 약간 수정하여 생성할 수도 있다.
Phase 7. 이웃탐색 실행 순서 이후의 m과 q의 무작위 배정
ai별로 직전 이웃탐색에서 배정된 m, q를 변경할 것인지 아니면 그대로 둘 것인지를 결정한다. 이 결정은 미리 설정한 변경확률과 0∼1 사이의 난수를 사용하여 결정한다. 만약, 발생한 난수가 변경확률 이하이면 cActi의 m과 q를 변경하고, 아니면 직전 이웃탐색에서 배정한 m과 q를 그대로 사용한다. m과 q의 변경 방식은 초기해를 구할 때와 동일하고, ai의 배정순서 생성과 초기해 생성과정은 초기 실행가능해를 생성할 때와 동일하다.
4.2.3 aimq의 조합 변경
각 Step에서는 cActi의 실행가능해 중 일부만을 변경하여 해가 향상될 수 있는 지를 검토한다. 만약 향상된다면, 해를 변경하여 향상된 실행가능해로 만든다. 예를 들어, Step 1에서 생성된 초기 실행가능해의 목적함수 값을 sVal라 하여 다음의 과정을 실행한다.
Phase 1. aimq의 조합 변경 알고리즘
aimq의 조합 변경은 a1~aN별로 m, q를 변경하는 방법이다.
Step 0. m과 q를 변경하는 활동이 ai일 경우, ai = 1로 변경하고 Step 1로 이동한다.
Step 1.
(1) 현재 실행 가능한 해의 활동별 시작시기를 기초로 활동들의 배정순서를 작성한다. 단, ai와 동시에 시작하는 활동이 존재하면, 그 활동 중 ai의 배정순서를 가장 먼저 수행한다.
(2) 현재 실행 가능한 해에서 ai의 m과 q를 각각 1로 변경하고, Step 2로 이동한다.
Step 2. m과 q가 변경된 해 작성(이하 변경해)
(1) ai를 포함하여, ai보다 늦게 배정된 활동들의 시작시기를 미정으로 한다.
(2) ai부터 aN까지 배정순서에 따라 시작시기를 배정한다. 마지막 활동까지 배정되면 변경해가 완성된다.
(3) 변경해의 목적함수 값 sVal보다 향상되었으면, 변경해를 현재 실행가능해로 등록하고, sVal를 변경한 후 Step 4로 이동한다. 반대로 향상되지 않았으면, Step 3으로 이동한다.
Step 3.
현재 m, q가 마지막 조합 M(N), Q[N,M(N)]이면, Step 4로 이동한다. 그렇지 않으면, 활동의 오름차순에서 current(m, q)를 later(m,q)로 변경한 후 Step 2로 이동한다.
Step 4. ai = aN이면, 종료한다. 그렇지 않으면, ai를 1증가한 후 Step 1로 이동한다.
Phase 2. ai의 시작시기 변경
여기서는 ai~aN까지 각 활동의 시작시기를 앞당길 수 있는지 검토한다. 어떤 활동의 m, q를 그대로 유지하고 다른 활동들의 시작시기도 그대로 유지한 채, 자신의 시작시기만 당길 수 있다고 하자. 배정순서 상 뒤에 배치되었던 활동이 다른 활동에 영향을 미치지 않으며 전보다 앞쪽에서 수행된다면, 해의 목적함수 값이 나빠질 수 없다.
Step 0. 시작시기를 앞당겨 배정하려는 ai = 1로 하고 Step 1로 이동한다.
Step 1. ai의 시작시기를 앞당길 수 있는지 검토하고 다음의 조건을 충족하여 새로운 시작시점이 존재하는지 확인한다.
(1) 새로 시작되는 시점은 ai의 선행활동들의 종료시점보다 빠르게 배정할 수 없다.
(2) 새로운 시작시점에서 시작해도 ai를 수행하는 데 필요한 자원은 부족하지 않다.
(3) 새로운 시작시점은 기존 ai의 시작시점 보다 최소한의 기간 앞이다. n 세 가지 조건이 모두 충족하고 시작시점이 존재하면, 현재의 실행가능해에서 ai의 시작시점을 새로운 시작시점으로 수정하고 sVal를 다시 계산한다. 그렇지 않으면 Step 2로 이동한다.
Step 2. ai = an이 성립하면, 종료한다. 그렇지 않으면 ai+1 증가하고, Step 1로 이동한다.
Phase 3. 이웃탐색 반복 여부 확인
위의 “Phase 1. aimq의 조합 변경 알고리즘”에서 (1)과 (2)를 거치는 동안 한 번이라도 실행 가능한 해가 개선되었다면, 다시 (1)과 (2)에서 해가 개선될 가능성이 존재한다. 만약, (1)과 (2)에서 개선되지 않았다면, 다시 (1)과 (2)를 반복하여도 해가 개선될 가능성이 없다. (3)은 이웃탐색으로 더 이상, 해의 개선이 불가능하면 Step 1로 이동하여 새로운 초기해를 생성시키고, 해 개선이 가능하면 이웃탐색을 반복한다.
4.3 모의실험 결과
모의실험의 목적은 본 연구에서 제시되는 모형이 정합성이 있음을 증명하고, 알고리즘에서 소개하는 개선규칙들의 효율성을 입증하는 것이다.
4.3.1 모의실험 조건 설정
모의실험을 위하여 다음 <Table 4>와 같이 데이터를 구성하였다. QI는 m에서 선택 가능한 Q = 3이다. q =1의 품질영향계수는 0.5~0.8, q = 2의 품질영향계수는 0.9~1.1, q = 3의 품질영향계수는 1.2~1.5 사이의 값을 임의로 설정하였다. 자원의 종류와 aim에 대한 자원 요구량(rink)은 rink = random(0 ... 5)으로 설정하였다. 그리고, 프로젝트 마감시간(DT)와 지체 보상금(PC)을 설정하였다.
4.3.2 최적화 알고리즘 실험결과
본 연구에서는 문제의 크기가 작은 경우(N = [6, 8, 10]) 최적화 알고리즘을 적용하여 시험결과를 도출하였다. 이는 문제가 크면 컴퓨터 연산시간에 한계가 있기 때문이다(Carolin and Helber, 2015). 최적화 알고리즘의 최적해를 도출하는데 소용되는 탐색시간을 문제의 크기별로 조사하였다. 각 샘플 프로젝트의 파라메타는 N = [6, 8, 10], M = 2, Q = 3 그리고, 샘플의 수P = 10으로 실험하였다.
<Table 6>의 경우 비용에 대한 표준편차는 N = 6인 경우 537, N = 8인 경우 451, N = 10인 경우 391로 나타났다. N의 크기가 증가하면서 비용의 크기는 크게 되지만, 표준편차는 점점 작아지는 것으로 나타났다.
4.3.3 이웃탐색 휴리스틱 알고리즘 실험결과
본 연구에서는 휴리스틱 알고리즘 효율성의 척도로 해의 정확성(최적해 값으로부터의 오차율)을 기반으로 4.2.2의 최적화 알고리즘 실험 중 N = 10인 결과를 사용하였다.
이웃탐색 휴리스틱 알고리즘은 3가지 Case로 구성되었다. (1) 활동별 모드, 품질수준 그리고 배정순서를 임의로 정한 뒤 해를 구하는 것이다. (2) 실행가능해에서 모드, 품질수준을 변경시켜 해를 개선해서 해를 구하는 것이다. (3) 실행가능해에서 시작시기를 앞당겨 해를 개선해서 해를 구하는 것이다. 여기서, Case[1]은 (1)을 반복한 후 가장 좋은 해 값을 구하는 방법이다. Case[2]는 (1)과 (2)를 포함하여 해를 구하는 방법이다. Case[3]은 (1)과 (2), (3)을 포함하여 해를 구하는 방법을 의미한다.
(1) 최적화 알고리즘과 휴리스틱 알고리즘의 비교 실험결과
최적화 알고리즘과 휴리스틱 알고리즘의 정합성 분석을 위해 프로젝트 샘플은 10개로 선정하였고, 활동의 수는 N = [6, 8, 10]으로 최적 알고리즘과 휴리스틱 알고리즘을 비교할 수 있도록 하였다. 여기서 휴리스틱 알고리즘의 연산시간은 10(sec)로 설정하여 휴리스틱 알고리즘 해를 도출하였다.
<Table 6>에서 최적해와 Case간의 평균은 Case[1]에서는 13,658으로 0.38(%) 차이를 보였다. Case[2]에서는 10,391으로 0.06(%) 차이를 보였다. Case[3]에서는 10,315으로 0.05(%) 차이를 보였다. 표준편차 또한, Case[1]은 3826.60로 0.37(%), Case[2]는 614.09로 0.04(%), Case[3]은 502.82로 0.03(%)의 차이를 보였다.
여기서, 최적해와 Case간 비교한 결과, 유효한 조건이 늘어날수록 그 차이는 축소되고 있음을 보여주고 있다. 무엇보다도 유효한 조건이 1개인 Case[1]과 유효한 조건이 3개인 Case[3] 간의 평균차이는 (-3,343)로 확연한 차이가 존재함을 알 수 있다. 이러한, 차이는 최적해의 33.96%에 해당하므로 유효한 조건을 발견하여, 적용하는 것이 필수임을 증명하는 것이다. <Figure 3>은 그 차이의 확실함을 보여주고 있다. 따라서, 휴리스틱 알고리즘 기법의 유효한 조건이 많을수록 최적해에 수렴되는 값을 얻을 수 있다는 것이다.
(2) 이웃탐색 알고리즘의 Case적용 실험결과
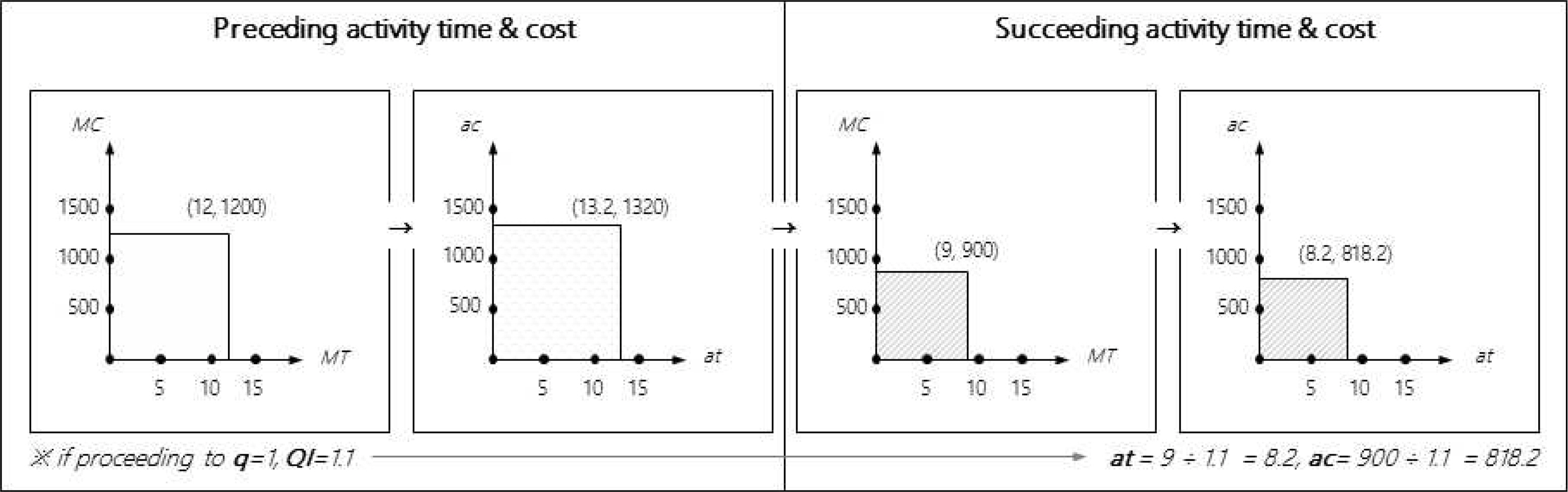
이웃탐색 알고리즘에 대한 정합성 검증을 위해 위의 3가지 Case을 적용하여 실험하였다. 프로젝트 샘플은 각각 10개로 선정하였으며, 활동의 수 N = [20, 30, 40, 50, 60, 70]으로 6가지의 프로젝트로 구성하였다.
이웃탐색 알고리즘의 Case적용 실험결과 <Table 7>과 같이 Case[3]의 결과가 가장 우수하게 나타났다. 특히, Case[1]의 해와 Case[3]의 해 차이는 N의 수가 증가할 수록 점점 증가되는 것을 알 수 있다. 무엇보다도 N = 20에서 Case[1]과 Case[3]의 차이는 25%에서 N = 70일 경우 73%의 차이가 나타났다. 이러한 결과는 <Figure 4>에서 그 차이를 확인할 수 있다.
따라서, 휴리스틱 알고리즘의 실험결과는 알고리즘의 모델을 어떻게 설계하고 적용하는가에 따라 알고리즘에서 제시하는 목적함수 값이 변경되는 것을 알 수 있다. 즉, 알고리즘 설계의 중요성을 시사하는 결과라 하겠다. 이것은 본 연구에서 적용한 프로젝트 일정에서 활동들의 품질 문제의 중요성을 증명하는 결과라 하겠다.
5. 결론
본 연구에서 모의실험을 통하여, 최적화 알고리즘의 경우 고품질 적용에 의한 효율성 결과를 얻을 수 있었고, 휴리스틱 알고리즘의 경우 알고리즘 모델 설계에 따라 최적해와 차이를 보이는 결과를 얻을 수 있었다.
최적화 알고리즘의 경우 N = 6일 경우 평균 탐색시간은 6.74초 소요되었고, N = 8일 경우 평균 탐색시간은 277.53초 소요되었다. N = 10의 평균 탐색시간은 10,807.37초로 나타났다. 이는 활동의 수와 모드, 품질수준의 수가 증가되면 활동들의 선ㆍ후행관계가 매우 복잡한 형태로 구성되기 때문에 탐색시간이 크게 증가되는 특징이 있음을 알 수 있었다.
특히, 최적화 알고리즘과 휴리스틱 알고리즘 모의실험 결과는 <Table 8>과 같이 휴리스틱 알고리즘에서 제시된 해와 최적해의 차이에 대한 결과로, 활동의 수가 증가되면서 최적해와 차이가 커지는 것을 알 수 있었다. 그러나, 이웃탐색 휴리스틱 알고리즘에 적용된 Case중에서 Case[3]이 우수한 결과를 얻었다. 이는 알고리즘에 적용되는 연산시간 증가와 알고리즘 모델을 어떻게 설계하느냐에 따라서 제시되는 해가 변경됨을 알 수 있었다.
최적화 알고리즘에서는 Blazewicz(1978), Duggan et al.(2004)의 연구와 같이 활동의 수가 증가됨에 따라 문제의 크기가 매우 큰 문제(NP-hard class)라는 것을 증명하였고, 모드와 품질영향계수의 수에 따라서 그 경우의 수 또한, 급증한다는 것을 증명하였다. 휴리스틱 알고리즘에서는 이웃탐색 알고리즘을 통해 연산시간의 증가로 인해 최적해 값에 가까운 해의 값을 얻을 수 있었고, 문제의 수를 증가함으로써 분석의 효율을 확인할 수 있었다. 이는 Masanori and Suzuki(2010), Carolin and Helber(2015)의 연구와 같이 모든 알고리즘 모델이 어떠한 모델을 어떻게 설계하는가에 따라 그 모델에서 제시되는 해의 신뢰는 변경될 수 있음을 시사한다. 또한, Icmeli-Tukel and Walter(1997), Elham et al.(2014), Madjid et al.(2014)의 연구와 같이 개별 프로젝트 일정문제의 활동에 품질수준을 적용하고, 분석하여, 전체적인 프로젝트 일정에 영향이 미친다는 것을 증명하였다. 따라서, 본 연구는 프로젝트 일정문제에서 다루지 않았던 선행활동의 품질이 자신 및 후행활동의 기간과 비용에 미치는 영향을 최적화 알고리즘과 휴리스틱 알고리즘에 적용한 모의실험으로 분석하였다는 것이 연구적 의의라 하겠다. 무엇보다도 원전 등 대형 프로젝트에서 예상하지 못한 위험요인이 발생이 되고 있다. 최고의 안전성을 가치로 여기는 산업의 특수성으로 인하여 설계, 구매, 건설과 시공 및 시운전까지 엄격한 품질 기준과 기술 요건이 필요하다(Yu et al., 2019). 따라서, 프로젝트를 진행하면서 품질의 중요성을 적용한다면 이러한 위험인자 등을 사전에 분석할 수 있을 것으로 기대된다.
최적화 알고리즘에서 실행 가능한 해를 빠르게 탐색하도록 할 수 있다면, 최적화 알고리즘의 성능은 매우 향상될 것이다. 본 연구에서 제시한 이웃탐색 알고리즘을 포함하여 타부탐색 알고리즘, 모의실험담금질 알고리즘, 유전자 알고리즘 등을 추가적으로 개발하고, 새로운 모델 설계를 적용하여 효율적인 알고리즘을 제시할 수 있을 것이다.
본 연구에서 최적화 알고리즘 모의실험은 N = [6, 8, 10]으로 제한하였다. 이는 실험을 위해 하드웨어 성능이 높은 컴퓨터를 사용한다면 활동의 수를 더 증가하여 실험 할 수 있을 것이고, 다양한 활동들에 대한 결과를 분석할 수 있을 것이다. 그러나 매우 큰 문제(NP-hard class)에 대한 연산부담은 여전히 해결해야 할 과제로 남는다. 본 연구에서 실험을 위해 사용된 모의데이터는 현실과 차이가 있을 수 있다. 따라서 보다 현실적인 데이터를 수집ㆍ분석하고 적용해야 하는 한계가 있다. 이는 알고리즘 모델에서 가능해를 어떻게 설정하는가에 따라 탐색부분이 결정되기 때문에 이를 보완하는 알고리즘 모델이 지속적으로 개발되어야 하겠다.