기동화력장비 관성항법장치의 효과적인 위치정확도 시험방법 개발
Development of Effective Test Method for Positioning Accuracy of Armed Vehicle Inertial Navigation System
Article information
Trans Abstract
Purpose
The main function of INS (Inertial Navigation System) is to measure the position of an armed vehicle and its performance is confirmed through the positioning accuracy test of Korean Defense Standards (KDS). The current standards, however, do not provide clear test methods and the conditions for performing positioning accuracy tests. Accordingly, the purpose of this study is to develop a new method for positioning accuracy test which would be effective.
Methods
In this study, a new INS positioning accuracy test method is suggested based on the analysis of test data collected through a statistical experiment known as central composite design. For the positioning accuracy experiment of K105A1, a self-propelled artillery, two factors of driving velocity and driving distance are considered.
Results
Based on the analysis of experimental data, a regression model for the positioning error is fitted and the positioning accuracy test of INS is so developed to maximize the positioning error. The standard proximity rate is used as an additional test criterion to evaluate the performance level of INS.
Conclusion
The proposed new positioning accuracy test for INS has the advantage of finding the nonconforming items effectively. It is also expected to be utilized for the other similar INS positioning accuracy tests.
1. 서 론
관성항법장치는 무기체계의 위치와 자세를 측정하는 중요한 역할을 한다. 특히 위치측정과 관련된 성능 항목은 국방규격에서 중요한 검사 항목으로 다루어진다. 그러나 현재 기동화력장비에 장착되는 관성항법장치의 성능평가와 관련한 규격은 위치정확도의 성능을 평가하기 위한 시험방법과 조건이 명확하지 않고 합격, 불합격 판정기준만 명시되어 성능평가에 있어 논란의 소지가 존재하고 있다.
일반적으로 시험평가 규격에는 시험설비, 시험방법 및 조건, 시험 결과에 대한 판단 기준 등이 상세하게 명시되어 있고, 정해진 성능시험 항목에 따라 제품에 대한 성능평가를 수행하게 된다. 자주포 주요 품목 중 하나인 계기판 내부 습기 발생 현상을 개선하기 위한 연구에서도 기존에 정해져 있는 성능 항목으로 성능을 평가하고 개선 방안을 입증(Nam et al., 2020)하였으며, 자주포용 장전 장치 밸브류를 국산화한 연구(Ko et al., 2020)에서도 시제품 성능을 확인하기 위해 정해진 규격 항목을 적용하였다. 또한 궤도차량의 변속 오류를 개선하기 위한 품질개선 연구(Yun et al., 2023)에서도 변속기의 문제를 정확하게 파악하기 위해 정해진 규격 항목을 토대로 시험을 실시하였다.
이처럼 규격 항목은 명확하고 성능평가에 있어 미리 정해져 있어야 논란의 소지를 줄일 수 있으며 성능평가 기준 뿐만 아니라 품질개선 활동에서도 기존 제품과의 비교 기준으로도 활용될 수 있다.
관성항법장치의 경우, 성능평가를 위한 다양한 시험 방법들이 연구되었으며 특히 항공 분야에서 많은 연구가 이루어졌다. 관성항법장치의 위치정확도를 평가하기 위해 항공 분야에서는 1시간이 넘는 비행 후 제자리로 돌아와 관성항법장치의 위치정확도 성능을 평가하는 RER(Radial Error Rate) 방식을 권장(Baek et al., 2016) 하였으나, 한정된 시간에 많은 장비를 검사해야 하는 기동화력 분야에 적용하기에 한계점이 존재한다. 또한 관성항법장치와 관련된 대부분의 연구는 관성항법장치 초기정렬 설계 및 평가 관련 연구(Yu et al., 2015), 관성항법장치 회전주기 선정 관련 연구(Kim et al., 2018) 등과 같이 개발 초기에 관성항법장치 단품을 다루거나 관성항법장치에서 필연적으로 발생하는 오차에 대한 특성을 분석하고 이를 보정하기 위한 설계적인 연구(Choi et al., 2023)가 다수이며, 양산성 및 검사, 성능평가 관점에서의 연구는 찾아보기 힘들다.
이 연구에서는 기동화력장비에 장착된 관성항법장치의 위치정확도 성능 확인을 위한 시험 평가 방법을 설계하고자 하며, 이를 위해 중심합성계획법을 이용하여 실험 후 구한 데이터로부터 위치정확도와 위치정확도에 영향을 미치는 인자와의 관계식을 구하고 위치정확도의 오차를 최대로 하는 시험조건을 도출하였다. 또한 규격근접률이라는 새로운 측도를 도입하여 기존의 모호한 시험방법을 대체할 수 있는 효과적인 관성항법장치 위치정확도 시험방법을 제시하였다.
2. 관성항법장치 주요 구조 및 위치정확도 시험
2.1 관성항법장치 주요 구조 및 작동원리
이 연구에서 다루고자 하는 관성항법장치는 Talin 4000 INS로 주로 자주포에 사용되고 있으며 외관은 Figure 1과 같다. Talin 4000 INS는 3차원 관성 공간에 위치한 물체의 각속도를 측정하는 자이로스코프와 선형 가속도를 측정하는 가속도계로 구성되며 측정된 신호를 처리하는 집적회로, 외부 하우징 등으로 구성된다.
Talin 4000 INS (Inertial Navigation System)
자이로스코프는 관성 공간에 위치한 물체의 회전각을 측정하기 위한 센서이다. 기본형태는 중심축과 무게중심을 고정 후, 중심축이 공간의 어느 방향으로도 자유롭게 회전할 수 있도록 하는 구조이다. 이에 물체의 움직임에 의해 각속도량이 측정 가능한 전압의 형태로 변환될 수 있도록 주변 장치들을 장착한 것이 관성항법장치에 적용된 자이로스코프이다. 가속도계란 물체에 동력이 작용 될 때 가속력과 방향을 이용하여 중력가속도를 기준으로 움직임의 변화를 측정하는 센서이다. 가속도계가 장착됨으로써 물체가 이동하는 정도를 신호형태로 인식할 수 있게 되며, 이를 토대로 물체가 어떠한 속도로 얼마만큼 이동했는지에 대한 정보를 얻을 수 있다. 이 연구에서 다루고 있는 위치정확도는 가속도계의 성능에 영향을 받는 성능이며, 가속도계가 정확하지 않을 때 오차가 크게 발생한다.
관성항법장치의 기본원리는 관성 센서를 통해 물체의 각속도와 가속도에 대한 정보를 측정하고 이를 좌표변환, 적분 등의 수학적인 연산을 통해 거리와 자세 등의 항법 정보를 제시하는 것이다. 적도를 횡축, 자오선을 종축으로 하는 국제 평면 직각 좌표계(UTM)의 개념에 따라 기준점으로부터의 동쪽 방향을 동거, 북쪽 방향을 북거라 하며 물체가 이동했을 때의 동거와 북거를 측정하고 시간 및 가속도 토대로 적분 연산하여 속도를 산출한다. 이렇게 산출 된 속도를 다시 적분하여 이동 거리를 알 수 있다. 결론적으로 동쪽과 북쪽에 대한 방향, 속도, 시간에 대한 정보가 모두 존재하므로 실제 물체의 이동 거리를 계산할 수 있는 것이다. 더불어 각속도를 측정하고 물체의 회전 정보를 획득하여 속도, 거리 정보와 종합되어 최종적으로 물체의 항법 정보로 제시된다.
2.2 관성항법장치 위치정확도
2.2.1 위치정확도 정의 및 중요성
위치정확도란 특정 위치의 이미 알고 있는 정확한 좌표값(측지점)을 기준으로 관성항법장치가 그 위에 위치할 때 얼마나 그 위치를 정확하게 인식하느냐에 대한 개념이며 발생 오차를 산출해 합격 여부 판정에 활용한다. 관성항법장치는 연속적으로 물체의 관성을 측정하며 움직임을 계산하는데 측정된 가속도 적분을 통한 위치 산출 방식이므로 연산이 반복적으로 수행될 경우 필연적으로 오차가 발생하고 누적된다. 체계장비 기준으로 설명하면 운용시간이 길어져 이동 거리가 증가할 경우 연산 횟수가 증가하며 오차가 발생할 수 있다.
자주포 및 전차는 자신의 현재 위치를 사격지휘소에 보고하고 사격지휘소에서는 적의 위치 정보를 토대로 정확한 사격제원을 계산한다. 이처럼 사격제원이 계산 및 하달되는 과정이 있기 때문에 관성항법장치의 위치 정보는 사격에 가장 중요한 정보이다. 당연하게도 위치정확도는 높은 수준을 유지하여야 하고 K9자주포를 비롯 자주포계열 장비에 사용되는 관성항법장치는 위치측정의 정확도가 높다.
2.2.2 현재의 위치정확도 시험방법
앞서 언급한 바와 같이 관성항법장치가 현재 위치를 정확하게 측정하는가에 대한 시험을 위치정확도 시험이라 하며 오차는 측정된 위치 값과 Figure 2의 측지점과의 차이로 산출한다. 측지점의 세부 좌표는 Eastern/Northern Point 값으로 주어지나 군 보안상 구체적인 수치는 명시하지 않았다. 이렇게 산출된 오차가 규격에 명시된 기준 안에 있을 때 합격 판정을 받는다. 위치정확도 시험은 군으로 납품하기 전에 시험장 환경에서 실시하며, 이때의 시험 절차는 다음과 같다.
Geodetic Point at Test Site
1) 먼저 관찰자는 위치 좌표값을 정확히 알고 있는 Figure 2의 측지점을 최초 출발점으로 삼고, 이 위에 자주포 앞바퀴를 위치시켜 관성항법장치가 현재의 위치를 인식하도록 위치 보정한다.
(측지점 좌표값과 사격통제장치에 전시된 위치보정 후 값이 일치하도록 조정한다.)
2) 위치보정이 완료되면 주행 시험로를 수차례 반복하여 주행한다. 이때의 자주포의 주행거리와 주행속도는 시험 수행자 및 검사자 간의 협의에 따르며 10km 이상의 주행을 권장한다.
3) 자주포의 주행이 완료된 후, 최초 출발점으로 돌아와 동일한 위치에 자주포 앞바퀴를 위치시킨다.
이때 사격통제장치에 전시된 위치 좌표값을 기록한다.
4) 최초 출발점인 측지점의 좌표와 시험 후 기록한 위치 좌표값의 차이를 통해 오차값을 산출한다.
그러나 현재 규격에는 명확한 주행거리 및 주행속도가 명시되어 있지 않아 실무적인 협의로 거리와 속도가 결정된다. 또한 규격에는 오차범위를 기준으로 위치정확도의 판단 기준만 명시되어 품질검사 및 관리 측면에서 어려운 점이 존재한다.
3. 위치정확도 실험설계 및 결과 분석
3.1 중심합성계획법을 활용한 위치정확도 실험설계
실험계획법은 다양한 분야에서 한 개 이상의 설계 변수와 반응변수 사이의 함수관계를 추정하고 최적 조건을 구하는 데 많이 사용되며, 실험계획법을 이용한 연구는 국방 분야에서 활발히 수행되었다. 직교배열표를 이용한 실험을 토대로 자주포 궤도 트랙슈의 충격 인성에 대한 강건설계를 다룬 연구(Kim et al., 2015), 포의 내부 강선설계 최적화를 위해 실험계획법을 활용한 연구(Kang et al., 2012), 전투차량의 지뢰 방호 구조설계가 폭압충격 특성에 미치는 영향을 파악하기 위하여 실험계획법을 통해 시험 방식을 설계하고 획득한 데이터에 대하여 분석을 수행한 연구(Park et al., 2018) 등 문제해결 및 최적화 등을 위해 실험계획법을 활용한다. 국방 분야 이외에도 중심합성계획법을 이용한 PoN 블록체인 시스템의 분산합 알고리즘의 성능 최적화 연구(Choi et al., 2021) 등이 활발하게 이루어지고 있다.
이 연구에서도 자주포의 관성항법장치 위치정확도와 설계 변수와의 함수관계를 파악하고 최적 조건을 구하기 위하여 실험계획법의 일종인 중심합성계획법을 적용하였다.
3.1.1 실험 목적 및 대상
체계장비를 기준으로 효과적인 위치정확도 시험방법과 조건을 도출하기 위해 중심합성계획법(Montgomery, 2020)을 활용하여 성능을 확인하되 검사자 입장에서 가장 오차값이 크게 발생하는 조건을 찾고자 하였다. 즉, 관성항법장치의 위치정확도 최적화는 위치정확도 오차가 최대가 되는 시험조건을 찾는 것이며 이를 바탕으로 위치정확도 시험방법을 설계하는 것이다. 오차가 가장 큰 설계변수 및 조건을 찾아낸다면 그 설계변수와 조건들은 제품을 검사하고 성능의 합격, 불합격을 판단하는데 적은 시험횟수로도 판정을 내릴 수 있는 효과적인 시험조건으로 간주할 수 있기 때문이다. 실험에 활용한 관성항법장치는 미국 Honeywell 사에서 제작한 Talin 4000 모델로 링레이저 자이로 방식이며 정격전압은 18-32Vdc, -46℃~71℃의 온도 조건에서도 작동이 가능하며, MTBF는 50,000시간, 크기는 14×19×22cm이며 중량은 약 6kg으로 자주포 계열 무기체계에 활용 중이다.
본 실험에서 활용된 체계 장비는 K105A1자주포이다. K105A1자주포는 1960년대 활용되던 105mm 견인 곡사포의 포를 일부 개조하여 군용차량에 탑재한 무기체계로서, 자동사격통제시스템, 관성항법장치 등이 적용되어 사격 및 신속한 진지변환이 가능하며 2010년대 말부터 야전에 배치되기 시작하였다. 주행실험은 자주포 생산업체의 주행시험장에서 실시하였으며 총 주행로 길이는 1바퀴가 약 1.6km, 폭은 00m, 포장도로이며 연속 주행이 가능하도록 양쪽 끝에 반환점이 있는 환경이다.
3.1.2 설계 변수 및 반응변수 선정
설계 변수는 주행거리(x1), 주행속도(x2)로 하였고, 반응변수(y)는 주행 후 위치정확도 오차값으로 선정하였다. 주행거리가 증가할수록 관성항법장치에서 계산되는 오차가 누적되고 주행속도가 빠를수록 변화량이 심해져 위치정확도 오차가 크게 발생할 것으로 예상하였기 때문이다. 위치정확도의 오차가 크게 발생할 수 있는 조건을 찾아내기 위하여 GPS는 미연동하고 변속기 출력단에 위치한 속도센서(VMS)만 연동하였다.
3.1.3 설계 변수의 수준 설정
주행거리(x1)는 주행이 끝나면 최초의 측지점으로 돌아와 오차를 산출하는 실험방법을 고려하여, 시험장 1바퀴의 거리를 기준으로 주행거리를 구분하여 6.4-16.0km(4-10바퀴)로 범위를 선정하였다. 또한 자주포의 최고속도 및 주행 간 안전 확보 등을 고려하여 주행속도(x2)는 32.0-48.0km/h의 구간으로 선정하였다. 최종 실험설계 조건은 중심점에서 3회 반복 시험을 포함한 Table 1과 같으며, 주행로 거리 1.6km를 고려하여 각 실험 조건에서의 거리는 1.6km의 배수로 선정하였다. 중심합성계획법에서 설계 변수가 2개인 경우에 일반적으로 중심점에서 5회의 반복 실험을 진행하지만, 이 연구에서 다루고 있는 자주포 관성항법장치 사례에서는 현장의 제약조건, 방산업체의 업무적인 특성 등을 고려하여 중심점에서의 반복 실험을 3회로 설정하였다.
Driving Test Conditions for Central Composite Design
3.1.4 실험 절차
위치정확도 실험을 위해 실험 절차를 수립하여 각 조건마다 동일한 실험방법을 적용하여 오차값을 확인하였다. 먼저 실험 대상인 K105A1자주포를 측지점에 좌측 앞바퀴를 위치시킨다. 주행 전후로 자주포가 일정한 장소에 위치할 때 관성항법장치가 인식하는 위치를 기준으로 모든 데이터를 작성하기 위함이다.
그 이후, GPS 통신케이블을 분리하여 GPS와 관성항법장치가 연동되지 않도록 한다. 앞서 설명했듯이 오차가 크게 발생하는 주행속도와 주행거리를 알기 위한 실험조건을 구성하기 위함이다. 통신케이블을 분리할 경우, 차량의 변속기 출력단에 위치한 속도 센서(VMS)만 연동되는 상태가 구현되며 위치정확도 측정은 2.2.2의 시험방법을 따르되 Table 1의 주행 실험 처리조합에 따라 주행거리와 주행속도를 변경하며 주행하였다.
하나의 실험 조건에 따라 주행을 마친 후에는 다시 최초 출발점인 측지점으로 돌아와 주행 시작점에 위치시킨 후, 통제장치에 나타나는 좌표 값을 결과지에 기록하였다. 동거, 북거 좌표를 기록하고 오차 산출식에 따라 오차값을 계산하였다. 해당 과정을 모든 실험 조건에 따라 반복하였다. 축점에서 4회, 꼭지점에서 4회, 중심점에서 3회로 총 11번의 실험을 수행하였다.
3.2 위치정확도 실험 결과 분석
3.2.1 관성항법장치 위치정확도 실험 결과
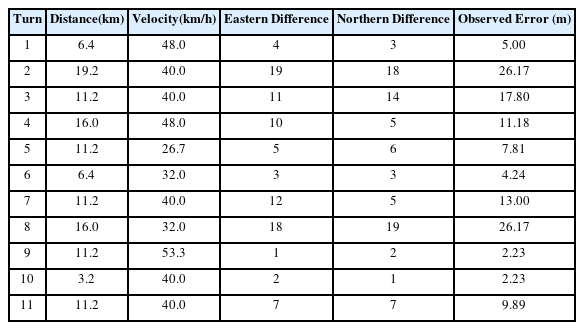
앞서 결정된 실험 조건별 주행 실험 처리조합에 따라 주행한 후, 각 조합에 관측한 관성항법장치 위치정확도 오차 값은 Table 2와 같다.
Driving Test Results for Positioning Error
위치오차가 가장 크게 발생한 조건은 설계 변수인 주행거리가 19.2km, 주행속도가 40.0km/h인 경우와 주행거리 16.0km, 주행속도가 32.0km/h인 경우이며, 이때의 위치정확도 오차값은 26.17m로 나타났다. 또한 주행거리 11.2km, 주행속도 53.3km/h 조건과 주행거리 3.2km, 주행속도 40km/h 조건에서 위치정확도 오차는 2.23m로 오차 값이 가장 작은 것으로 나타났다. 중심점인 주행거리 11.2km, 주행속도 40km/h에서의 3회 실험값은 오차가 차례로 17.80m, 13.00m, 9.89m로 확인되었다. 전체 11회의 주행실험에서 확인된 위치 오차값은 모두 규격 이내인 것으로 확인되었다. 아울러 기대했던 대로 주행거리가 길어질수록 발생하는 위치정확도 오차값이 커지는 경향을 보였으나 주행속도의 경우에는 이차곡선 형태의 오차값 변화가 나타났다.
3.2.2 위치정확도 오차값 반응모델 추정 및 적합성 평가
실험데이터를 바탕으로 반응변수인 위치오차 y 에 대해 적합한 회귀모형은 식(1)과 같이 도출되었으며, 유의수준 5%에서 유의하지 않은
ANOVA for Positioning Accuracy
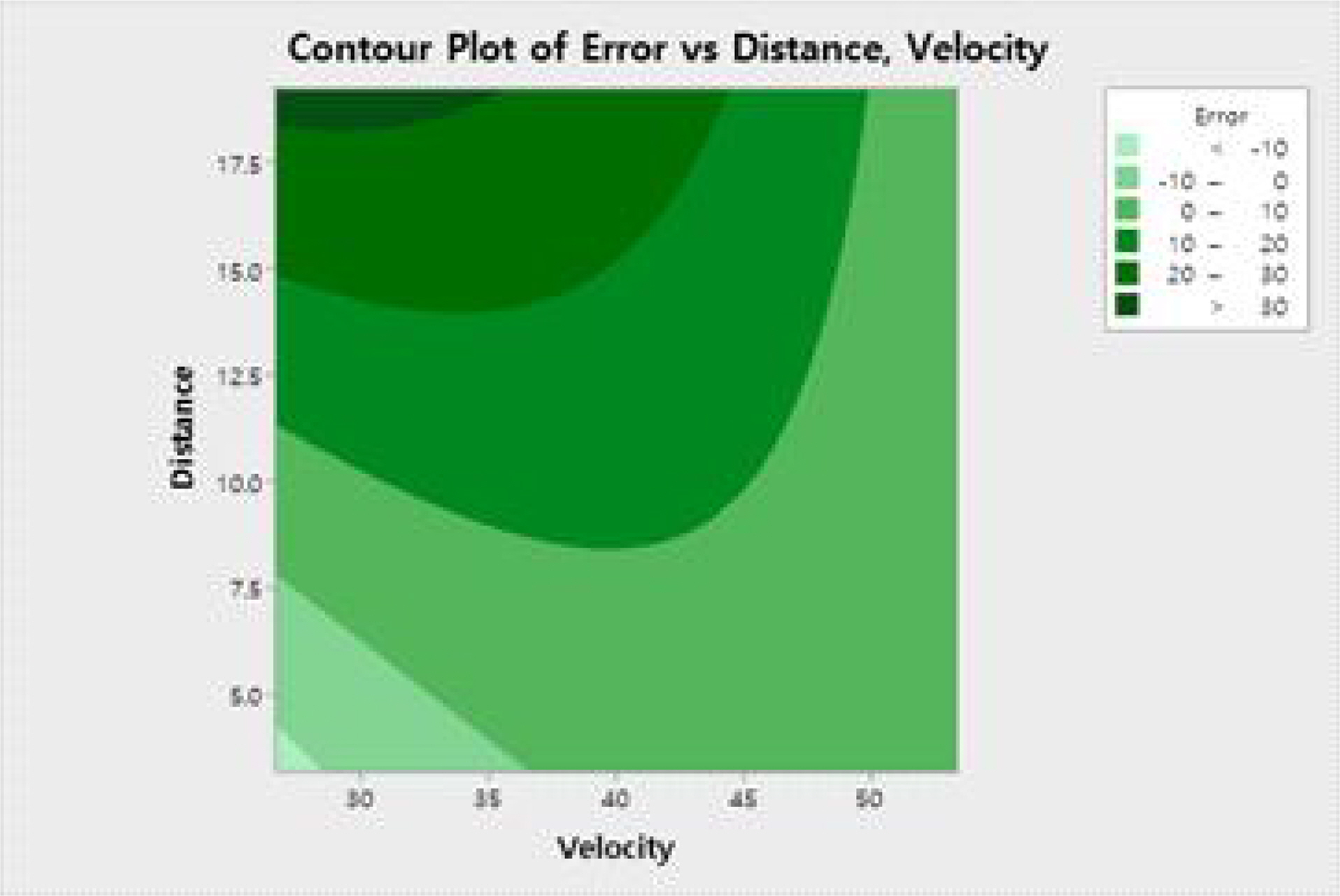
아울러 이 회귀모형의 R2 값은 94.3%이며 적합 결여 검정의 P-값은 0.931로 유의수준 5%에서 현재 회귀모형이 적합함을 확인할 수 있다. 위의 분산분석 결과를 함께 고려할 때 식 (1)을 이용하여 반응변수 y에 대한 예측을 수행함에 충분하다고 판단된다. 반응변수 y에 대한 회귀식을 이용한 등고선도와 반응표면 그림은 Figure 3, 4와 같으며 주행거리가 길수록, 주행속도가 느릴수록 위치정확도 오차가 증가하는 경향을 보인다.
Contour Plot of Positioning Error
Surface Plot of Positioning Error
4. 관성항법장치의 효과적 위치정확도 시험방법 설계
4.1 위치정확도 최대오차 발생 시험조건 도출
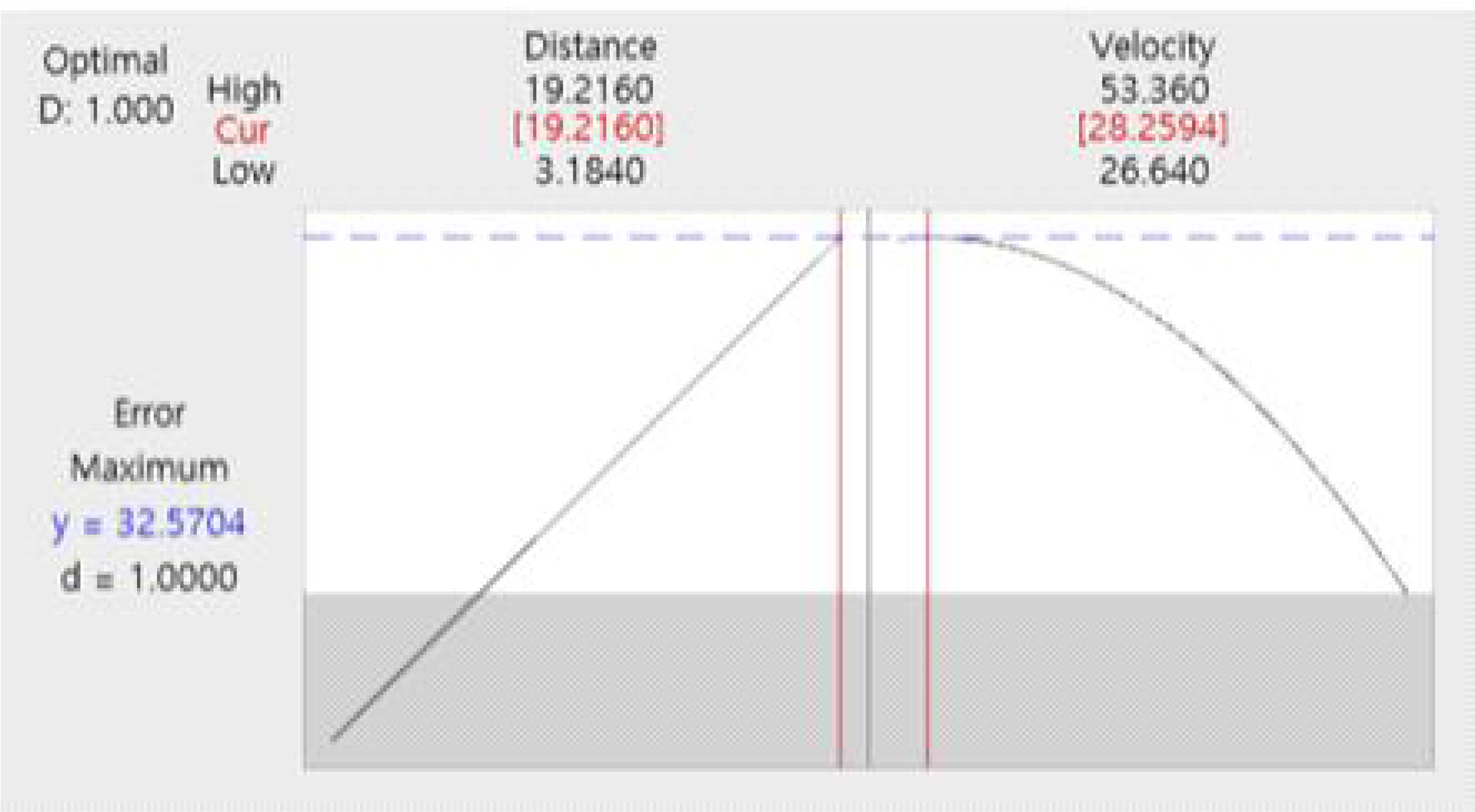
이 연구에서는 위치정확도의 최대오차 발생 조건을 찾고 이를 바탕으로 관성항법장치의 위치정확도 시험조건을 설계하고자 한다. 이는 품질검사 및 관리 측면에서 오차가 크게 발생하는 조건으로 시험하는 경우 관성항법장치 성능에 대한 판별력이 증가하기 때문이다. 이에 따라 Figure 5와 같이 최대오차가 발생하는 최적조건을 Minitab 21의 망대특성에 대한 반응 최적화를 활용하여 도출하였다. 위치정확도 실험 결과 분석에서 도출된 회귀모형을 기준으로 주행거리가 19.2km이고 주행속도가 28.3km/h일 때 위치정확도 오차값이 가장 크게 발생할 것으로 예상되었다.
Optimal Condition for Maximum Positioning Error
4.2 위치정확도 최대 규격근접률 발생 조건 도출
실제 자주포의 위치정확도는 주행거리가 길어질수록 오차가 크게 발생하는 것은 가속도계의 신호처리 메커니즘 상 당연한 결과라고 판단된다. 그러나 이 연구에서는 품질검사 및 관리의 관점에서 살펴봄으로 실제 오차값이 얼마나 큰 값이 나오느냐에 대한 부분과 더불어 실제 규격에 명시된 값과 얼마나 차이 나는지도 확인하고자 하였다.
그 이유는 현재 규격에 명시된 오차의 허용범위 값이 특정한 거리 00m가 아닌 주행거리의 0.00% 이내로 명시되어 있어 주행거리에 따라 오차값의 판단 기준이 계속 변하기 때문이다.
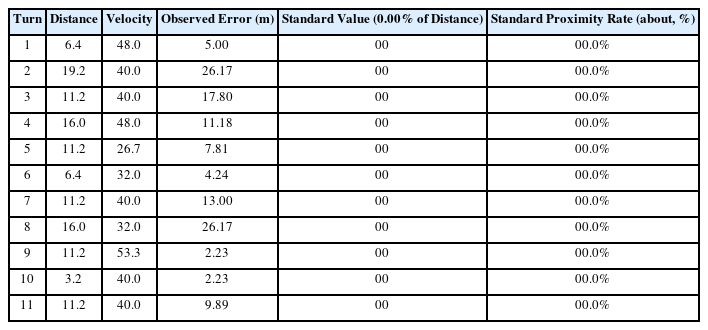
이에 따라 이 연구에서는 규격과 결과값의 비율인 규격근접률이라는 새로운 개념을 도입하고 규격근접률의 최대 발생 시험조건을 구하였다. 규격근접률을 산출하는 계산식은 식 (2)와 같으며 실제 주행을 통해 도출되는 오차값과 규격을 비교하여 규격에 얼마나 근접하느냐를 고려하여 0~100%의 값으로 산출한다. 100%에 가까운 규격근접률일 때는 규격과 오차값이 상당 수준 근접하므로 규격을 벗어날 위험성이 높아지는 것으로 판단할 수 있으며 이를 낮추기 위한 활동이 필요함을 알 수 있다. 반대로 규격근접률이 낮을수록 규격과 오차값은 많은 차이가 나며 이는 품질변동에 대한 여유가 확보된 것으로 판단할 수 있다. 주행 실험 결과 얻어진 규격근접률 관측값은 Table 4와 같다(군 보안상 규격근접률의 구체적인 수치는 명시하지 않았다).
Driving Test Results and Standard Proximity Rates Calculated
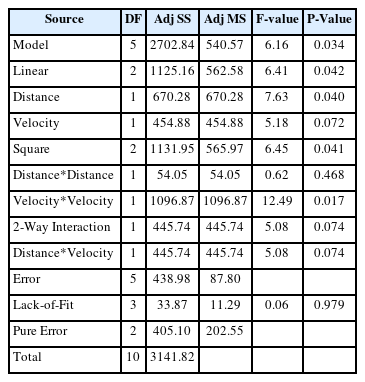
Table 4의 결과를 바탕으로 규격근접률에 대한 회귀모형을 식 (3)과 같이 도출하였고, 분산분석 결과는 Table 5와 같다.
ANOVA for Standard Proximity Rate
분산분석을 수행한 결과 규격근접률에 대한 회귀모형의 R2값은 0.860으로 나타났으며, 유의수준 5%에서 주행거리, 주행속도*주행속도 항만이 통계적으로 유의한 것으로 나타났다. 그러나 규격근접률에 대한 회귀모형은, R2값을 고려하여 주행속도, 주행거리*주행거리, 주행거리*주행속도 항을 모두 포함하였다. 또한 모형에 대한 적합 결여 검정의 P-값은 0.979로 추정한 회귀모형의 적합함을 확인하였다.
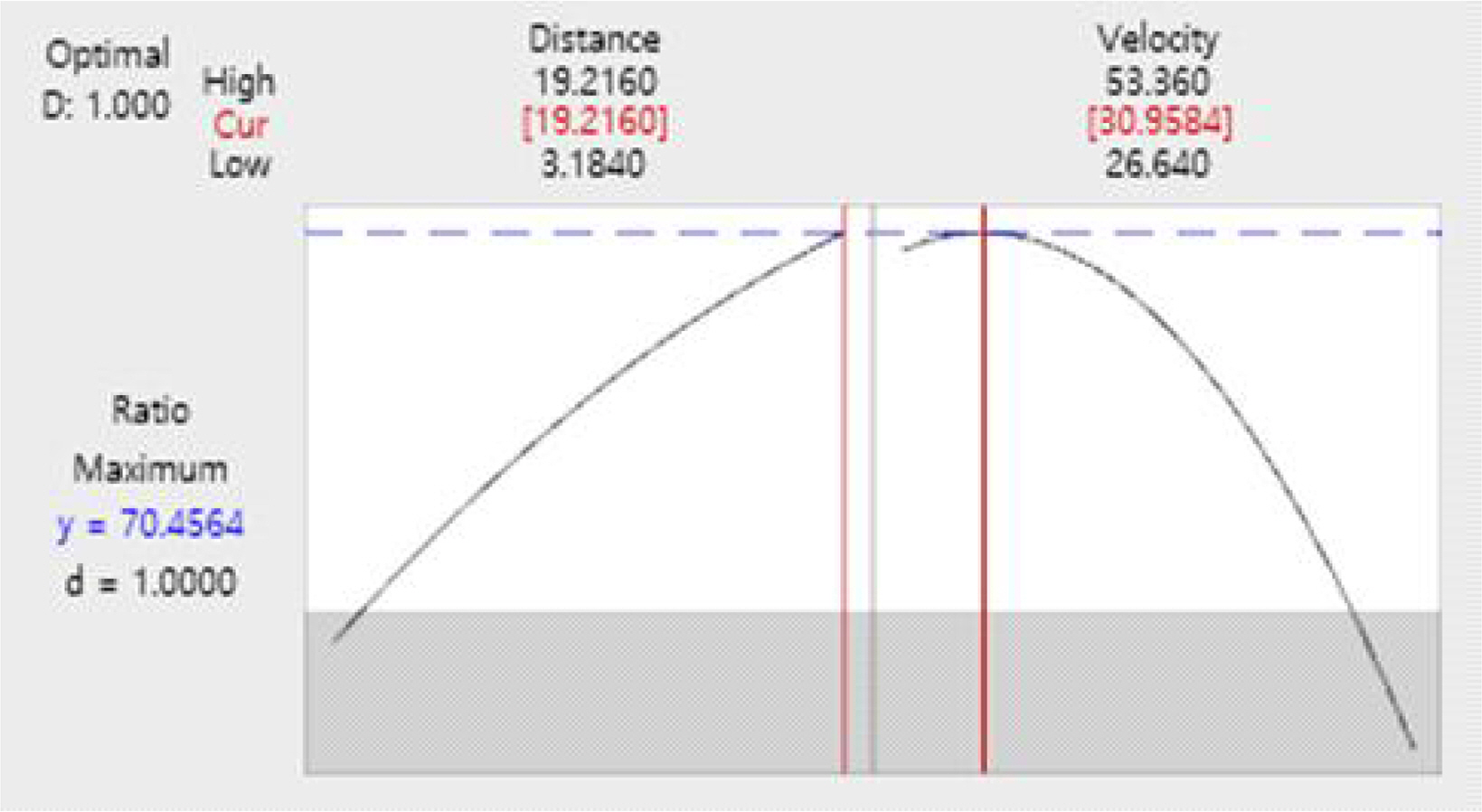
위치정확도 실험 결과 분석과 마찬가지로 도출된 회귀식을 활용하여 Figure 6과 같이 최대 규격근접률이 발생하는 조건을 구해보면 주행거리는 19.2km, 주행속도는 30.9km/h이며 규격근접률은 70.5%로 산출되었다. 이는 해당 시험조건에서 발생하는 오차값이 크고 규격과 가장 근접함을 의미한다. 이 조건을 활용한다면 시험 대상품에 대한 규격 판정과 더불어 품질에 대한 수준을 확인할 수 있다.
Optimal Condition for Maximum Standard Proximity Rate
위치정확도 오차와 규격근접률이 최대로 되는 조건은 주행거리가 19.2km로 동일하며 주행속도의 경우 각각 28.3km/h와 30.9km/h로 약 2.6km/h 만큼 차이가 난다. 이는 자주포가 낼 수 있는 최고속도와 주행로의 노면 상태, 바람의 방향 등 주행시험 환경 및 운전자 숙련도 등을 고려하였을 때 시험에 있어 2.6km/h의 속도 차이는 동등한 수준으로 판단되어 최대오차 발생 조건과 최대 규격근접률을 동시에 만족하는 조건으로 주행거리 19.2km, 주행속도 28~30km/h로 선정하였다.
이를 토대로 새롭게 설계한 효과적인 관성항법장치의 시험방법 및 순서는 다음과 같다.
(1) 측지점을 출발점으로 하고 관성항법장치가 이를 인식하도록 위치를 보정한다.
(2) 위치를 보정한 후 주행거리를 19.2km, 주행속도를 28~30km/h로 유지하며 주행한다.
(3) 주행 후 출발점에 위치시켜 자동사격통제장치에 전시된 위치 좌표 값을 기록한다.
(4) 측지점과 시험 결과값의 차이를 통해 오차값을 산출하고 규격과 비교하여 합격/불합격을 판단한다.
(5) 규격근접률을 산출하여 70% 미만인지 확인하고 만약 70% 이상일 경우 추가시험을 실시한다.
(6) 추가시험 이후 결과 값에 대한 규격근접률이 70% 미만일 경우 시험을 종료한다.
새롭게 제시한 시험방법은 현재의 모호한 관성항법장치 시험조건을 대체하여 실무에 바로 적용이 가능하며 최대 오차가 발생하는 조건을 찾아 위치정확도 시험의 판별력을 증대할 수 있는 효과가 있다. 또한 규격근접률의 개념을 적용하여 제품 고유의 성능에 대한 품질수준을 가늠할 수 있어 안정적인 무기체계 성능 발휘 등 유익한 영향을 미칠 것으로 기대된다. 그러나, 이 연구에서 제시한 시험방법에 대한 재현성 검증은 방산업체의 보안 및 업무적 특성 등의 제약사항으로 인하여 수행하지 못하였다. 재현성 검증에 대한 부분은 추후 자주포 관성항법장치에 대한 실제 시험 평가 단계에서 확인할 수 있을 것으로 예상된다.
5. 결 론
이 연구에서는 기동화력장비에 장착된 관성항법장치 위치정확도 실험 데이터를 바탕으로 품질검사 및 관리 측면에서의 효과적인 위치정확도 시험방법을 제시하였다. 먼저 위치정확도 오차에 영향을 미칠 것으로 예상되는 자주포의 주행거리와 주행속도를 설계 변수로 선정하고 이를 고려한 중심합성계획법을 통해 얻은 실험 데이터를 바탕으로 위치정확도 오차와 설계 변수 간의 회귀모형을 구하였다.
주행실험 결과 발생하는 위치정확도 오차값은 주행거리가 길수록 크게 발생하며, 주행속도가 느린 구간에서 오차가 크게 발생하는 경향을 확인할 수 있었다. 또한 추정된 회귀모형을 이용하여 최대 오차발생조건과 최대 규격근접률 발생조건을 도출하였으며 이를 토대로 새로운 위치정확도 시험방법을 제시하였다. 최종적으로 Talin 4000 관성항법장치의 위치정확도 성능을 확인하기 위한 효과적인 시험조건은 주행거리 19.2km, 주행속도 28-30km/h 수준이며, 규격근접률 산출을 통해 제품의 성능 수준을 파악하고 이를 검사 간 활용 하여 안정적인 성능이 나타나는 제품을 식별할 수 있게 하였다. 이와 같은 관성항법장치에 대한 시험방법을 활용한다면 기존 규격의 모호한 시험방법을 대체할 뿐만 아니라 기존 시험보다 적은 시험 횟수로도 유의미한 위치정확도 시험 결과를 확인할 수 있을 것으로 기대된다.