심층강화학습 기반의 경기순환 주기별 효율적 자산 배분 모델 연구
A Study on DRL-based Efficient Asset Allocation Model for Economic Cycle-based Portfolio Optimization
Article information
Trans Abstract
Purpose
This study presents a research approach that utilizes deep reinforcement learning to construct optimal portfolios based on the business cycle for stocks and other assets. The objective is to develop effective investment strategies that adapt to the varying returns of assets in accordance with the business cycle.
Methods
In this study, a diverse set of time series data, including stocks, is collected and utilized to train a deep reinforcement learning model. The proposed approach optimizes asset allocation based on the business cycle, particularly by gathering data for different states such as prosperity, recession, depression, and recovery and constructing portfolios optimized for each phase.
Results
Experimental results confirm the effectiveness of the proposed deep reinforcement learning-based approach in constructing optimal portfolios tailored to the business cycle. The utility of optimizing portfolio investment strategies for each phase of the business cycle is demonstrated.
Conclusion
This paper contributes to the construction of optimal portfolios based on the business cycle using a deep reinforcement learning approach, providing investors with effective investment strategies that simultaneously seek stability and profitability. As a result, investors can adopt stable and profitable investment strategies that adapt to business cycle volatility.
1. 서 론
4차 산업 혁명의 도래로 딥러닝과 강화학습 같은 혁신적인 기술이 금융 분야에 큰 변화를 가져오고 있다. 포트폴리오 최적화 분야에서도 기존의 전통적인 방법들을 뛰어넘는 발전이 이루어지고 있다. 이러한 변화 속에서, 심층강화학습(Deep Reinforcement Learning, DRL)은 최적의 결정을 학습하고 추론하는 능력을 갖춘 인공지능 모델로서, 금융 분야에서의 자산 배분 문제에 새로운 시각을 제시하고 있다. 포트폴리오 최적화는 투자자들이 수익을 극대화하면서도 위험을 효과적으로 제어하는 핵심적인 도전과제이다. 기존의 포트폴리오 최적화 모델들은 경기순환에 따른 자산의 성과 변화를 고려하지 않거나 정적인 가정에 기반하여 구성되는 경우가 많아 왔다. 이러한 문제를 극복하고 변동성 있는 경제 환경에서도 견고하고 적응적인 투자 전략을 모색하기 위해, 본 연구에서는 심층강화학습 기반의 효율적 자산 배분모델(Deep Reinforcement Learning-based Efficient Asset Allocation Model: DREAM)을 제안한다. DREAM은 경기순환주기의 변화를 고려하여 포트폴리오 배분을 동적으로 조정함으로써 최적의 수익과 위험 관리를 동시에 추구한다. 이를 통해 투자자들은 다양한 경기 상황에 유연하게 대응하며 안정적인 수익 창출의 기회를 얻을 수 있다.
본 연구의 목적은 경기순환주기에 따른 자산 성과의 변화를 DRL을 통해 모델링하고 이를 기반으로 최적의 포트폴리오를 구성하는 DREAM을 개발하고 검증하는 것이다. DREAM은 현재 경제 상황의 변화를 실시간으로 감지하고 분석하여 자산 배분을 동적으로 조정함으로써 투자자들이 변동하는 시장 환경에 빠르게 대응할 수 있도록 지원한다. 더불어, DRL의 학습 능력을 활용하여 기존의 정적인 가정에 의한 모델보다 효율적이고 유연한 포트폴리오 최적화를 실현한다. 본 연구는 자산 배분의 심층적인 연구와 혁신적인 포트폴리오 최적화 방법의 개발에 기여하고, 이를 통해 투자자들은 수익 극대화와 위험 관리를 조화롭게 달성하는 효율적인 투자 전략을 구축하고자 한다.
2. 이론적 배경 및 선행연구
2.1 포트폴리오이론(Portfolio Theory)
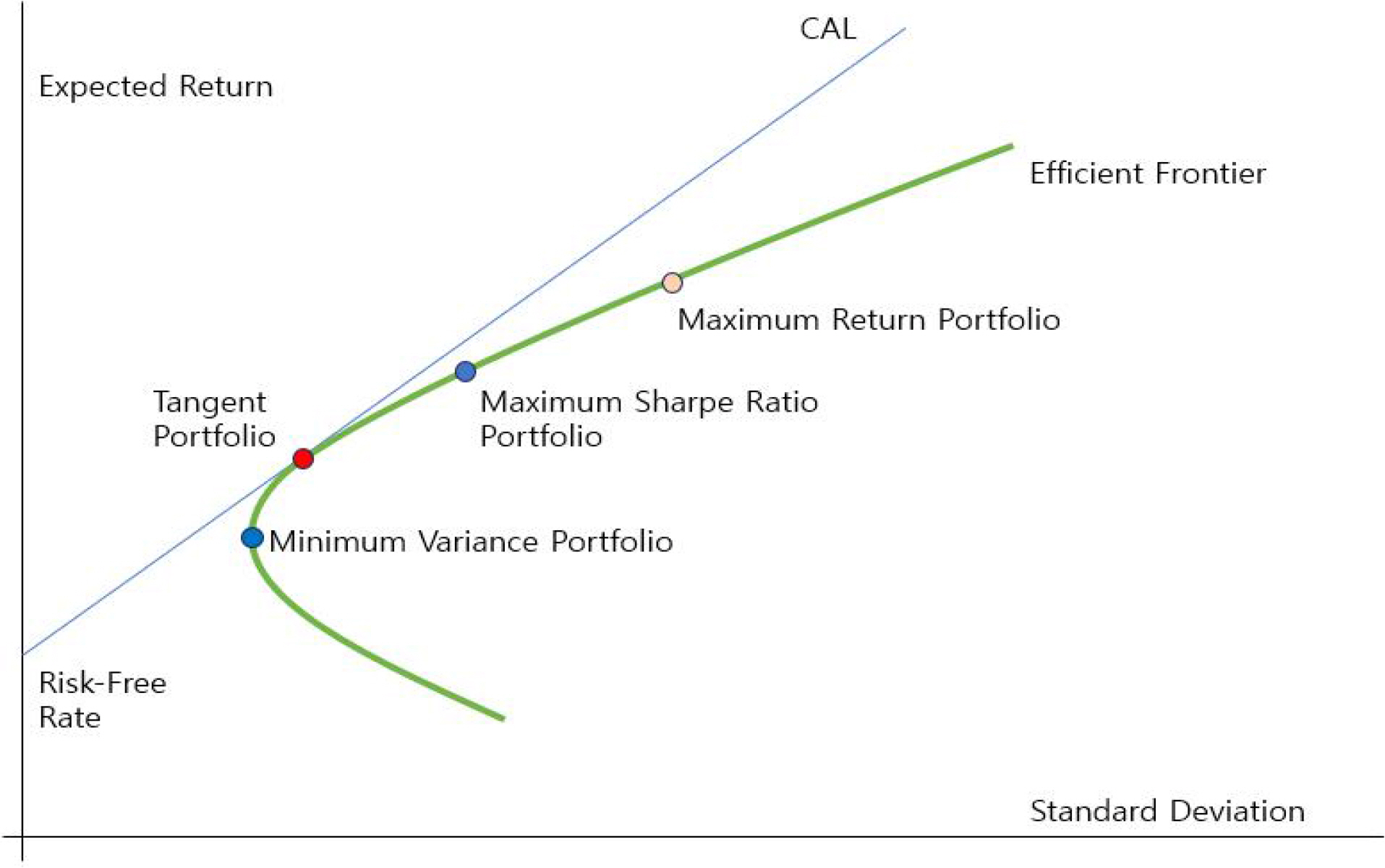
포트폴리오이론은 투자자들이 여러 개의 자산으로 구성된 포트폴리오를 구성함으로써 예상 수익과 위험을 최적화하는 방법을 연구하는 이론이다. 이 이론은 효율적 자산 배분이라고도 불리며, 다양한 자산들의 조합을 통해 투자자들이 원하는 수익 대비 최소의 위험을 얻을 수 있도록 한다(Markowitz, 1952). 이 이론은 투자자들이 투자하는 자산 간의 상관관계를 고려하여 포트폴리오의 다양성을 증가시킴으로써 위험을 분산시키고 수익률을 극대화할 수 있는 최적의 자산 배분을 찾는 것을 목표로 한다(KIM, Kim, and Kang, 2016). 포트폴리오에서 각각의 투자 비율에 따라 포트폴리오의 기대수익률과 위험(표준편차)의 변화를 그림으로 나타낼 수 있는데, 이것이 포트폴리오 결합선(Portfolio Combination Line)이다. Figure 1.의 경우는 무위험자산(risk-free)이 포트폴리오에 포함된 경우를 보여준다. 이러한 포트폴리오 결합선 상에서 위험이 최소가 되는 포트폴리오를 최소분산 포트폴리오(Minimum Variance Portfolio: MVP)라고 한다(Markowitz, 1952). 이차 곡선이 옆으로 누워 있는 모습이 바로 이 포트폴리오 결합선이자 효율적 투자선(Efficient Frontier)이고, 가장 좌측의 값이 MVP이다(Markowitz, 1952). 자본배분선(Capital Allocation Line: CAL)이란, 무위험자산과 위험자산 사이의 투자 비중을 변동시킬 때 기대 수익률과 투자위험의 조합을 나타낸 선이다(Markowitz, 1952). CAL과 MVP가 접하는 경우, 가장 효율적인 투자 조합이다. CAL의 기울기가 가파를수록 효율적인 투자 기회임을 의미한다. 이렇게 가장 효율적인 CAL 그래프를 자본시장선(Capital Market Line: CML)이라고 한다. 자본시장선과 효율적 투자선이 접하는 점이 바로 접점 포트폴리오(Tangency portfolio)이며, 무위험자산으로 구성된 포트폴리오 중에서 가장 높은 샤프 지수를 가진 포트폴리오이다(Sharpe, 1998). Maximum Return Portfolio는 기대수익률을 최대화하기 위해 구성되는 포트폴리오로, 위험을 최대한 감수하고 수익률을 극대화한다. Maximum Sharpe Ratio Portfolio는 샤프 비율을 최대화하기 위해 구성되는 포트폴리오이다. 이 포트폴리오는 수익률과 리스크 사이의 균형을 고려하여 구성된다.
포트폴리오의 성과를 측정하고 비교하기 위해 주로 사용되는 지표로는 샤프 지수(Sharpe ratio)와 소르티노 지수(Sortino ratio)가 있으며, 두 지표는 포트폴리오의 수익과 리스크 간의 상호 관계를 파악하는 데 사용된다(Sharpe, 1998; Sortino and Van Der Meer, 1991).
샤프 지수는 포트폴리오의 위험 대비 수익률을 측정하는 지표로, 투자자들이 투자한 자산의 기대수익률을 투자한 위험으로 조정한 후의 수익률을 평가한다(Sharpe, 1998). 즉, 투자자가 감수한 위험 대비 수익을 얼마나 받을 수 있는지를 보여주는 지표이다. 샤프 지수는 식(1)과 같이 계산된다.
식(1)에서, Ri은 포트폴리오 수익률, Rf는 무위험수익률, Ri - Rf 는 포트폴리오 초과 수익률이며, σi 는 포트폴리오 수익률의 표준편차이다. 샤프 지수는 수치가 클수록 투자자가 위험 대비 초과 수익을 내는 것을 나타낸다. 무위험 이자율은 보통 정부 채권 등의 안정적인 투자에 대한 이자율을 사용한다. 따라서 샤프 지수가 높을수록 해당 포트폴리오는 더욱 효율적인 투자 전략으로 간주한다.
소르티노 지수는 포트폴리오의 하위 수익률에 대한 리스크 대비 수익률을 측정하는 지표이다(Sortino and Van Der Meer, 1991). 샤프 지수와 마찬가지로 투자 전략의 효율성을 평가하는 데에 사용되지만, 무위험 이자율 대신 하위 수익률을 기준으로 삼는다. 소르티노 지수는 식(2)와 같이 계산된다.
식(2)에서, Ri은 포트폴리오 수익률, Rf는 무위험수익률, Ri - Rf 는 포트폴리오 초과 수익률이며, σid 는 포트폴리오 수익률의 하락 리스크이다. 소르티노 지수는 투자 전략의 초과 수익(평균 수익률에서 하위 수익률로 간주 되는 수익률을 뺀 값)을 해당 전략의 하위 수익률의 표준편차로 나눈 값으로 계산된다. 이 지표를 사용하여 투자자들은 주로 하위 수익률에 대한 리스크관리 측면에서 정확한 효율성을 평가하고, 리스크를 줄이면서도 수익을 극대화하는 포트폴리오를 선택하거나 평가하는 데에 활용한다. 따라서 하위 수익률에 민감한 투자 전략의 성과 측정에 유용하게 사용된다. 높은 소르티노 지수는 더 안정적이고 위험을 줄인 투자 전략이다.
2.2 자산배분전략
자산 배분 전략은 투자자가 다양한 자산 클래스 또는 자산들을 어떤 비율로 구성하는지 결정하는 것을 말한다. 이는 투자자의 투자 목표, 투자 기간, 리스크 허용도 등을 고려하여 수익을 극대화하거나 리스크를 효과적으로 관리하기 위해 사용되는 전략이다. 자산 배분은 투자 성과에 큰 영향을 미치는 중요한 결정 사항 중 하나로, 투자 포트폴리오의 안정성과 수익률을 극대화할 수 있다. 자산 배분은 주로 주식(Equity), 채권(Bond), 현금(Cash), 대체 자산(Alternative Asset) 등을 대상으로 하며(Gu and Jang, 2010), 자산 배분의 접근방식은 통계적 기법, 시뮬레이션 기반, 심층강화학습 기반의 최적화 알고리즘 등을 기반으로 하는 전략을 수행한다.
먼저 통계적 기법은 다음과 같다. 최소분산 포트폴리오(Minimum Variance Portfolio)는 변동성을 최소화하는 포트폴리오 선택하고 주어진 자산들의 과거 수익률과 공분산을 기반으로 최적화하여 변동성을 최소화하면서 수익률을 극대화하는 포트폴리오 선택한다. 접점 포트폴리오(Tangent Portfolio)는 주식과 무위험자산을 조합하여 효율적 투자선을 찾고 리스크 대비 수익률을 최대화하는 Sharpe ratio를 최대화하는 포트폴리오 선택한다. 최소 변동성 포트폴리오(Mininum Volatility Portfolio)는 변동성을 최소화하여 가장 안정적인 수익을 추구한다.
몬테카를로 시뮬레이션(Monte Carlo Simulation)은 확률적인 방법을 사용하여 다양한 시나리오를 생성하고, 이를 통해 미래의 수익과 리스크를 예측하는 시뮬레이션 기법이다(Metropolis and Ulam, 1949). 주식 시장의 불확실성과 다양한 요인을 고려하여 포트폴리오 수익과 리스크를 계산하는 데 사용된다. 무작위로 생성한 시나리오들을 기반으로 투자 전략을 시뮬레이션하여 포트폴리오의 예상 수익과 리스크를 추정하는 방식이다.
본연구에서 포트폴리오 최적화를 위해 제안하는 심층강화학습(Deep Reinforcement Learning: DRL)은 강화학습과 딥러닝을 결합한 기술로, 에이전트가 환경과 상호작용하면서 최적의 행동을 학습하는 방법이다. DRL의 주요 모델은 다음과 같다. A2C(Actor-Critic)는 Actor-Critic 알고리즘의 변형으로, actor와 critic를 결합하여 최적의 행동을 학습하는 강화학습 알고리즘이다(Mnih et al., 2016). PPO(Proximal Policy Optimization) 정책 경사 알고리즘의 발전된 형태로, 안정적인 정책 업데이트를 목표로 하는 알고리즘이다(Schulman et al., 2017). DDPG(Deep Deterministic Policy Gradient)는 연속적인 행동 공간에서 작동하는 강화학습 알고리즘으로, Actor-Critic 구조를 사용한다. actor는 연속적인 행동을 생성하며, critic을 이용하여 행동의 가치를 평가한다(Lillicrap et al., 2015). SAC(Soft Actor-Critic)는 연속적인 행동 공간에서의 정책 최적화를 위한 알고리즘으로, 확률적 정책을 사용하여 불확실성을 고려한다. Entropy를 최대화하는 방향으로 학습하여 탐색을 촉진하고 안정적인 학습을 돕는다(Haarnoja et al., 2018). TD3(Twin Delayed Deep Deterministic Policy Gradient)는 DDPG의 변형으로, actor와 critic를 사용하여 최적의 행동을 찾는 알고리즘이다. 복수의 가치함수를 사용하여 학습을 안정화한다(Fujimoto et al., 2018).
2.3 경기순환과 자산수익율에 영향을 미치는 요인
경기순환 이론은 경제 현상을 네 단계로 나누어 설명하고 있으며, 경제는 회복기, 호황기, 후퇴기, 침체기라는 패턴을 순환 반복한다(Schumpter, 1939). 경제 전반을 파악하기 위한 지표는 경기종합지수(Composite Index of Business Indicators: CI)가 있고, 경기 반영 시차에 따라 경기선행지수(Composite Leading Index: CLI)와 경기동행지수(Coincident Composite Index, CCI), 경기후행지수(Lagging Composite Index: LCI)로 나누며, CI를 통해서 경기 현상에 대한 진폭과 전환점을 파악할 수 있다(Ko, 2021; Kim, 2015). CI는 경기 상승기와 경기 하강기에 전월 대비 증감률이 양(+)과 음(-)을 나타낸다. 또한 경기변동진폭의 크기를 통해서 경기국면, 경기전환점과 경기순환의 방향까지 분석을 할 수 있다(Kim, 2015). Chi(1998)의 연구에서는 주식이 경기순환주기를 9개월 선행하고, 채권은 6~8개월 경기순환주기를 후행하며, 12개월의 시차로 부동산시장은 경기순환주기를 후행한다고 분석하였다. Lee and Baek(2016)의 연구에서는 코스피 지수는 달러, 유로, 위안 및 엔 환율의 환율 변동과 다우존스지수와 국제유가의 관련성을 연구하였다(Lee and Baek, 2016). Li and Kim(2013)의 연구에서는 경기순환을 고려한 자산 가격 책정과 투자 전략의 중요성을 강조하였다. JUNG, Oh, and Kim(2023)의 연구에서는 통계청에서 나오는 경기종합지수 보완을 위해서 딥러닝을 이용하여 CLI와 CCI를 예측하는 합성보조지수를 연구하였다.
2.4 포트폴리오이론에 관한 연구
Gu and Jang(2010)은 주식, 채권, 예금을 이용하여 최적의 포트폴리오 구성과 교체전략의 연구를 하였고, Koo, and Lee(2013)의 포트폴리오 구성에 관한 연구에서는 주식형, 혼합형, 채권형, MMF의 펀드를 가지고 최적화 시뮬레이션과 평균분산 모형으로 자산 배분을 하는 연구를 하였다. Park and Shin(2013)의 연구에서는 포트폴리오 수익률을 최대로 하고 리스크를 최소로 하는 리밸런싱 방법을 제안하였다. Park, Lee, Rhee, and Jang(2014)의 연구에서는 베이지안 학습을 이용해서 경기순환주기를 반영한 자산관리모형을 제안하였다. Yang and Kang(2015)은 2008년 국제 금융위기 전후의 혼합 자산의 최적 포트폴리오를 구하는 연구를 하였으며, Mean-Variance 방법을 이용하여 리츠를 구성 종목으로 하는 혼합 자산의 최적 포트폴리오 비율을 도출하였다. Park and Cho(2015)는 유럽배출권 거래제(EU ETS)의 사례를 분석하여 탄소배출권의 효율적 투자선과 최적의 포트폴리오를 연구하였다. Kim and Kim(2015)는 유전자 알고리즘을 통해 포트폴리오의 투자자산의 위험을 GPD를 통해 추정하는 연구를 하였다. KIM et al.(2016)은 외환 포트폴리오의 예측모형을 베이지안 방법을 이용해서 선택하는 연구를 하였다. Song, Choi, and Kim(2017)의 연구는 SVM(Support Vector Machine)을 이용하여 상품 자산에 투자하는 모델을 연구하였으며, 골드만삭스, 다우존스 UBS, 톰슨로이터 CRB, 로저스 인터내셔날과 같은 대표적인 상품 지수와 에너지, 농산물, 금속 상품을 대상으로 SVM을 활용하여 투자 가능한 포트폴리오와 개별 상품 선물을 구성하였다. Kang, Bae, Yang, and Choi(2019)의 연구에서는 생애주기와 경기순환주기를 투자모형으로 고려한 TDF 펀드의 연구를 통해서 수익률과 안정성의 개선을 확인하였다. Kim and Ko(2021)의 연구에서는 KOSPI 200의 지수 종목 중 기대수익률이 높은 종목을 선정하고 포트폴리오를 구성하는 강화학습모델을 제안하였다. Lim, Cao, and Quek(2022)의 연구에서는 LSTM 예측 모델을 이용한 강화학습을 통해 포트폴리오 리밸런싱을 통한 성능향상을 확인하였다. Durall(2022)의 연구에서는 DRL과 전통적인 통계 기법을 이용하여 미국 주식으로 구성된 포트폴리오의 Bear Market과 Bull Market의 수익률을 비교하였다. Sood, Papasotiriou, Vaiciulis, and Balch(2023)의 연구에서는 최적의 포트폴리오 할당을 위해 DRL과 평균분산 포트폴리오(Mean-Variance Portfolio Optimization: MVO)간의 비교연구 결과 DRL의 성능이 샤프 지수, MDD 및 절대 수익에서 MVO 대비 우수한 성능을 입증하였다.
2.5 선행연구 분석 및 한계
선행연구들의 분석 결과는 다음과 같다. 첫째, 포트폴리오이론을 적용하여 투자자들이 수익과 리스크를 고려하여 최적의 자산 배분을 할 수 있다(Markowitz, 1952). 이는 다양한 자산 조합을 통해 원하는 수익 대비 최소의 위험을 추구하는 데 활용된다(Gu and Jang, 2010; Park and Shin, 2013). 둘째, 경기순환 주기를 고려하여 자산의 가격 및 투자 배분을 조정할 수 있으며, 경기순환의 변동성을 고려하는 것은 포트폴리오의 성과를 향상시킬 수 있다(Park et al., 2014). 셋째, 인공지능 기법, 특히 DRL과 같은 기술을 활용하여 최적의 포트폴리오를 구성하고 성능을 개선할 수 있다(Durall 2022).
선행연구의 한계점은 다음과 같다. 첫째, 많은 선행연구 들이 과거 데이터를 기반으로 하는 모델이다. 이로 인해 모델은 현재와 미래의 금융 시장 조건을 정확하게 반영하지 못할 수 있으며, 급격한 변동성이나 예측 불가능한 사건에 대응하기 어려울 수 있다(Kim and Kim, 2015; Song et al., 2017; Lim et al., 2022). 둘째, 경기순환주기에 대한 고려가 부족하다. Park et al.(2014)의 베이지안 학습 모델은 경기순환 주기를 고려한 자산 관리를 제안하지만, 데이터 의존성과 비선형성 처리의 어려움과 같은 한계점을 가지고 있다. Durall(2022)의 연구에서는 Bear Market과 Bull Market의 수익률을 단순 비교만 하고, 경기순환 주기에 적합한 최적화 모형은 제시하고 있지 않다. 셋째, 통계적방법을 사용한 최적의 포트폴리오 모델은 일정 기간의 데이터를 기반으로 하여 시간에 따른 변화를 고려하지 않고 정적인 최적화를 수행한다(Koo and Lee, 2013; Park and Shin, 2013). 선행연구들의 한계점을 극복하기 위해서, 본 연구에서는 DRL을 활용하여 최적의 포트폴리오를 구성하고 관리하는 방법을 제안하며, 샤프 지수 또는 소르티노 지수와 같은 보상 함수를 사용하여 최적화한다. 또한, 경기순환주기에 따라 적절한 보상 함수로 샤프 지수와 소르티노 지수를 활용하여 포트폴리오의 성과를 경기순환에 민감하게 조정하고 최적화한다. 학습된 DRL 모델을 테스트하여 성능을 평가하고 실무 적용 가능성을 고려한다.
3. 연구 방법
3.1 DRL-based Efficient Asset Allocation Model(DREAM)
본연구에서 제안하는 DREAM 모델을 수식으로 나타내면 식(3)과 같다. DREAM은 DRL을 사용하여 최적의 자산 배분 전략을 찾는 모델이다. 각 DRL 모델(AC2, PPO, DDPG, SAC, TD3)을 순회하며 세 가지 다른 전략인 Sharpe DREAM, Sortino DREAM, Sharpe-Sortino DREAM을 평가하고, 각 모델에 대해 가장 우수한 전략을 선택한다. 선택된 전략에 따라 효율적인 자산 배분을 하고, 성능을 평가한다.
각 모델은 다음과 같이 세 가지로 정의된다.
첫째, Sharpe DREAM 이다. 식(4)와 같이 포트폴리오 비율을 조정하여, 최대 샤프 지수를 구하는 DRL 모델이다. 이 모델은 리스크 대비 수익을 최대화하는 목표를 가지며, 더 안정적인 투자 전략을 찾아내는 데 중점을 둔다.
둘째, Sortino DREAM 이다. 식(5)와 같이 포트폴리오 비율을 조정하여, 최대 소르티노 지수를 구하는 DRL 모델이다. 이 모델은 하락 리스크를 고려하여 투자 수익 대비 하락 리스크를 최소화하는 목표를 가지며, 주식 시장의 불리한 리스크를 줄이는 방향으로 전략을 탐색한다.
마지막으로, Sharpe-Sortino DREAM 이다. 식(6)과 같이 경기순환주기를 고려하여 경기 상승기인 호황기와 회복기에는 최대 샤프 지수를 구하고, 경기하강기인 후퇴기와 침체기에는 최대 소르티노 지수를 구하는 DRL 모델이다. 이 모델은 경기 상황에 따라 최적의 전략을 적용하여 더욱 효과적인 자산 배분을 실현한다.
여기서, T는 학습 기간의 시간 스텝 수, st는 시간 스텝 t에서의 상태, at는 시간 스텝 t에서의 행동, θsharpe, θsortino, θsharpe-sortino는 각 모델의 학습 가능한 파라미터, Rewardsharpe(st,at;θsharpe)는 Sharpe DREAM의 보상 함수, Rewardsortino (st,at;θsortino)는 Sortino DREAM의 보상 함수, θsharpe-sortino (st,at;θsharpe-sortino)는 Sharpe-Sortino DREAM의 보상 함수이다. 각 모델은 학습 가능한 파라미터 θ를 조정하여 주어진 보상 함수를 최대화하는 방향으로 학습된다. 이를 통해, 각 모델은 주어진 자산 배분 문제에 대한 최적의 전략을 찾아가게 된다.
3.2 제안 모델 구축 방법
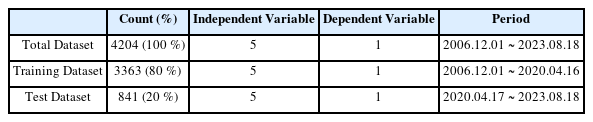
경기순환주기와 관련된 CLI와 CCI 데이터는 통계청에서 수집하고, 포트폴리오를 구성하는 주식 종목의 가격 데이터는 한국거래소에서 수집한다. 무위험 이자율 데이터는 0.02 로 가정한다. 수집한 데이터를 정제하고, 결측치나 이상치를 처리한다. 연구에 사용할 데이터는 Table 1.과 같으며, 연구 대상 기간은 2006.12.01. ~ 2023.08.18. 이다.
수집된 CLI와 CCI를 통해 경기순환주기를 정의하고, 해당 기간을 호황기, 후퇴기, 침체기, 회복기 등으로 구분한다(Schumpter, 1939). 본 연구에서는 경기순환주기를 판단을 CLI와 CCI의 순환변동치를 활용하여, 특히 CLI와 CCI의 상대적인 크기와 패턴을 기반으로 각각의 상태를 다음처럼 판단하기로 한다(Ko, 2021; Kim, 2015). 호황기는 CCI와 CLI 모두 100보다 큰 경우로 판단한다. 둘 다 큰 경우 경기가 호황에 있으며, 이때 CLI가 CCI보다 크면 더욱 강세의 호황기로 판단한다. 후퇴기는 CCI가 100보다 크지만, CLI가 CCI보다 작은 경우로 판단한다. 경기가 여전히 호황이지만 CLI에 비해 CCI가 약한 상황을 의미한다. 침체기는 CCI가 100보다 작고 CLI가 CCI보다 큰 경우로 판단한다. 침체기는 경기가 둔화되었으며, CCI에 비해 CLI가 높은 상태이다. 회복기는 CCI와 CLI 모두 100보다 작은 경우로 판단한다. 둘 다 작은 경우 경기가 회복 중인 상태를 의미한다. 본 연구에서는 위와 같은 기준을 토대로 경기 순환주기를 판단하고, 해당하는 순환 주기를 각 데이터에 할당한다. 수집한 데이터를 기반으로 DREAM 모델을 사용하여 최적의 자산 배분 전략을 학습한다. 각 DRL 모델 (AC2, PPO, DDPG, SAC, TD3)을 순회하며 세 가지 다른 전략인 Sharpe DREAM, Sortino DREAM, Sharpe-Sortino DREAM을 학습하고 평가한다.
3.3 제안 모델 성능 평가
DREAM 모델을 2006년 12월 1일부터 2020년 4월 16일까지 학습한 모델을 이용하여 2020년 4월 17일부터 2023년 8월 18일까지 모델별로 백 테스트(Backtest)를 수행하였다.
본 연구에서는 DRL 모델과 전통적인 통계 기법인 Minimum Variance, Minimum Volatility, Max Sharpe 모델을 성능 평가 지표들을 사용하여 평가하고 비교한다(Woo et al., 2023; Durall, 2022). 샤프 지수는 투자 수익 대비 리스크를 측정하기 위한 지표로, 높을수록 효율적인 투자를 나타낸다. 소르티노 지수는 주식 시장의 하락을 고려하여 투자 수익 대비 하락 리스크를 측정하는 지표이다. Cumulative Returns는 누적 수익률을 나타내며, 투자 전략의 전반적인 성과를 파악하는 데 사용된다. Annual Return는 연간 수익률을 나타내며, 투자의 연간 성과를 평가하는 지표이다. Annual Volatility는 연간 변동성을 나타내며, 투자의 변동성 정도를 측정하는 지표이다. Max Drawdown(MDD)는 최대 손실액을 나타내며, 투자 전략의 피크에서 가장 큰 손실을 겪을 가능성을 보여준다.
4. 연구 결과
4.1 기초통계량분석
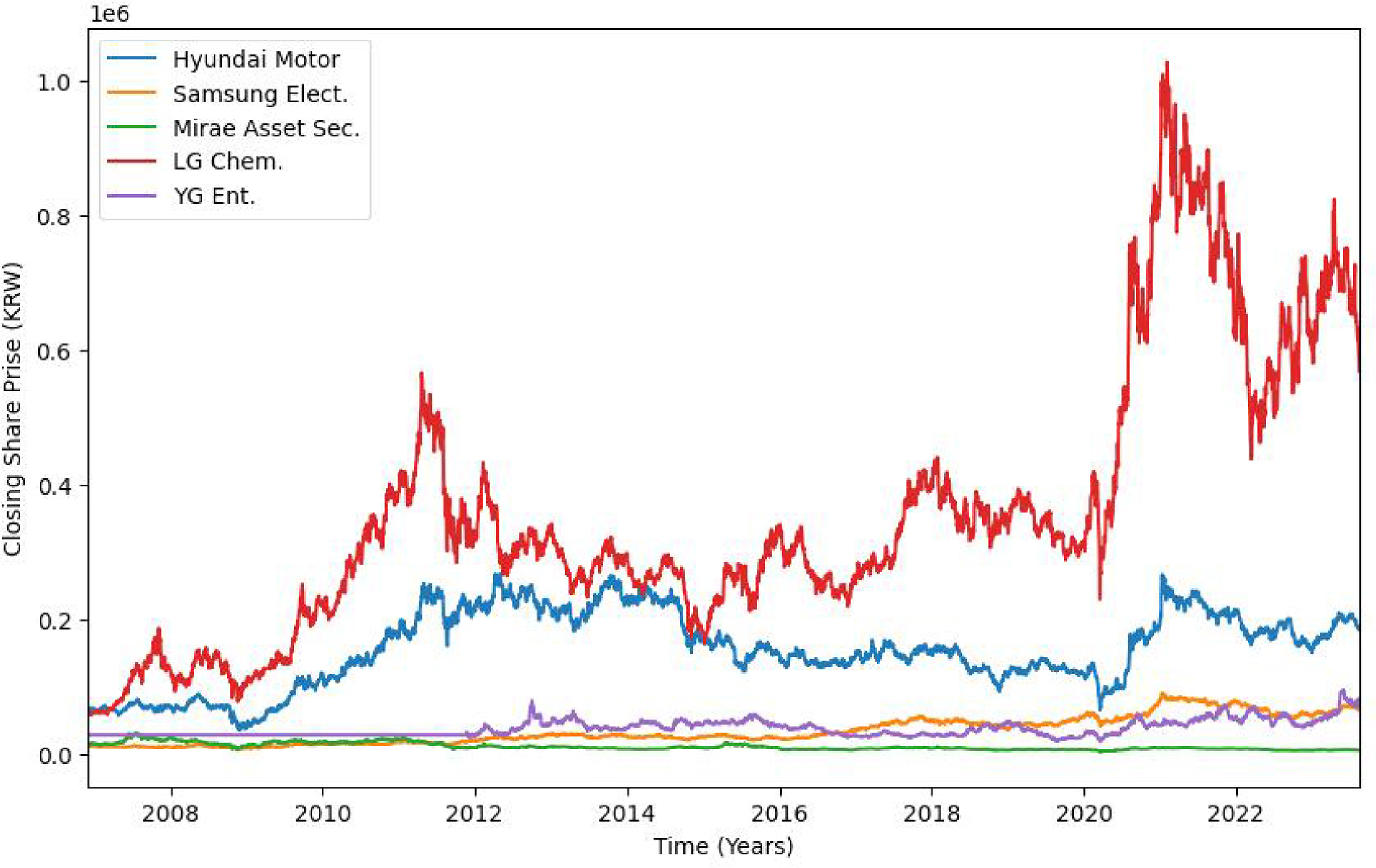
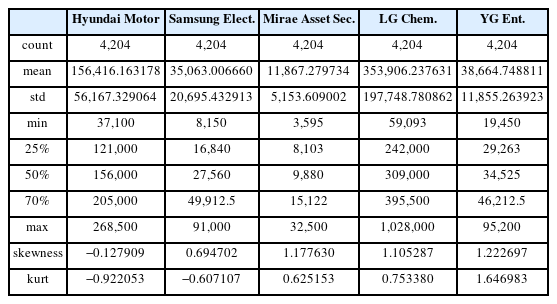
본 연구에서 사용하는 데이터는 다음과 같다. 첫째, CLI와 CCI 데이터는 통계청에서 수집하였다. 둘째, 연구를 위해서 임의의 포트폴리오를 구성하는 종목을 KOSPI 200을 구성하는 종목인 현대차(종목번호 005380), 삼성전자(종목번호 005930), 미래에셋증권(종목번호 006800) 및 LG화학(종목번호 051900) 과 KOSDAQ 종목인 YG엔터테인먼트(종목번호 122870)로 하고 가격 데이터를 한국거래소에서 수집하였다(Park and Shin, 2013; Kim and Ko, 2021). 휴일의 경우는 데이터가 없으므로 직전 영업일의 데이터를 가져와 사용하였다. 셋째, 데이터의 수집 기간은 2006.12.01.부터 2023.08.18.까지이고 주식 포트폴리오를 구성하는 자산들의 일자별 수익률은 Figure 2.와 같고, 수집된 주식 포트폴리오의 기술 통계량 데이터는 Table 2.와 같다.
4.2 연구 결과
4.2.1 경기순환 주기별 포트폴리오 최적화 결과
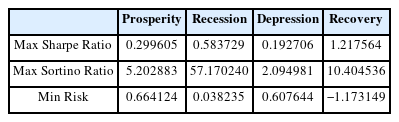
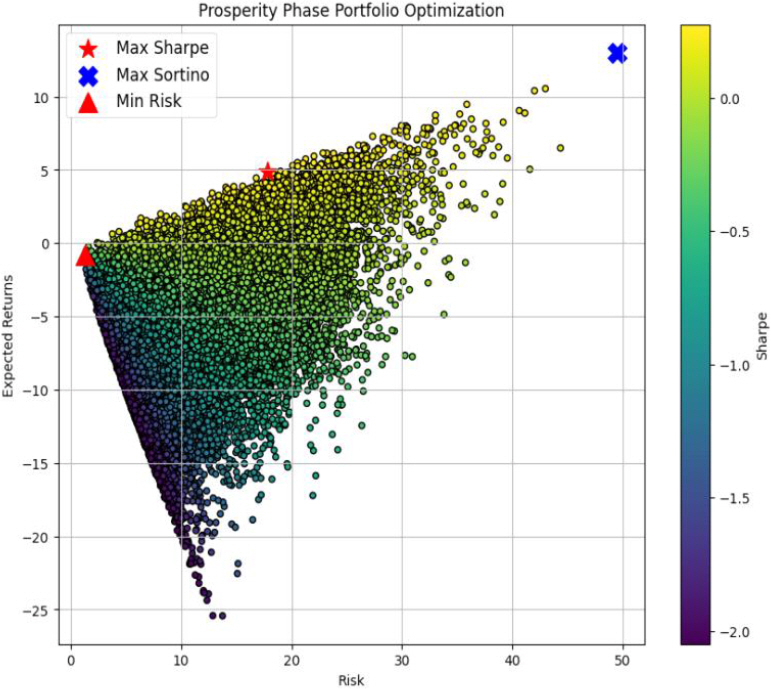
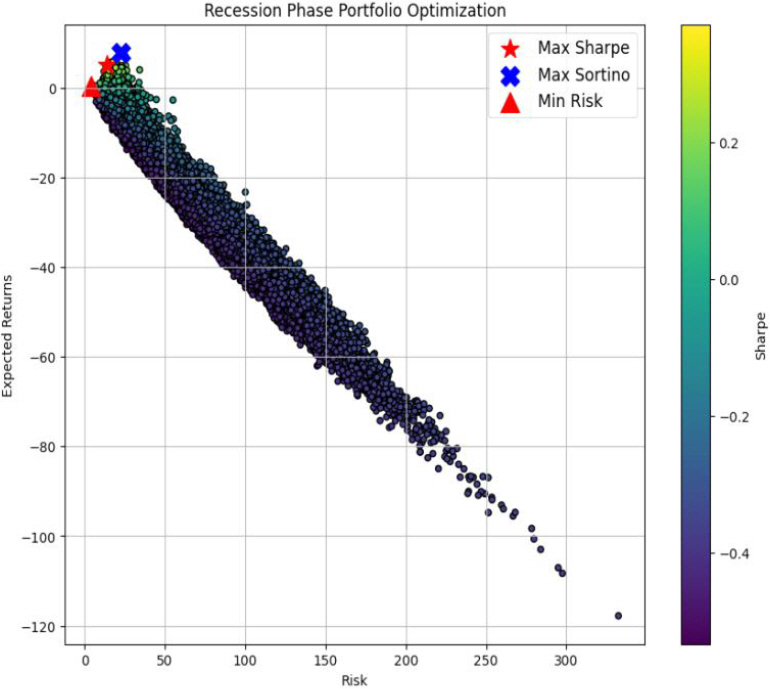
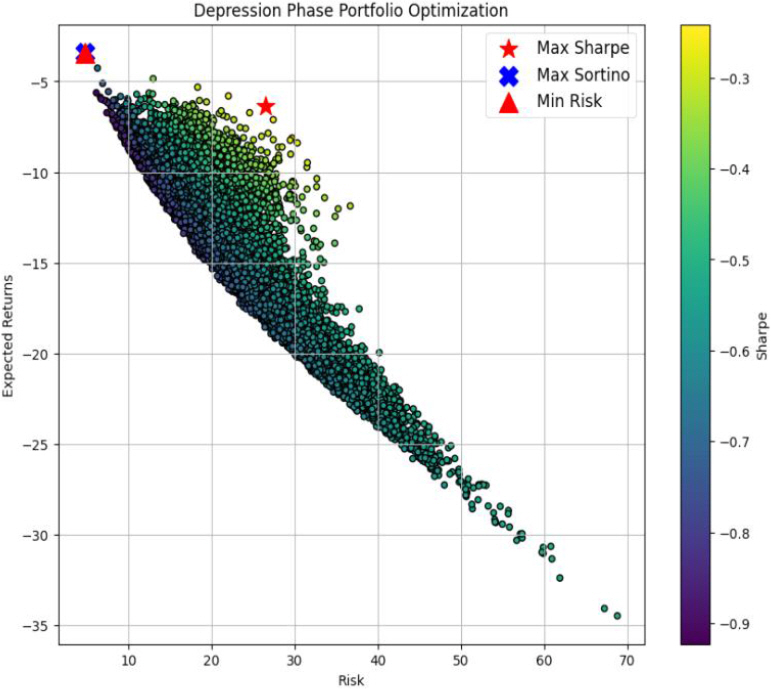
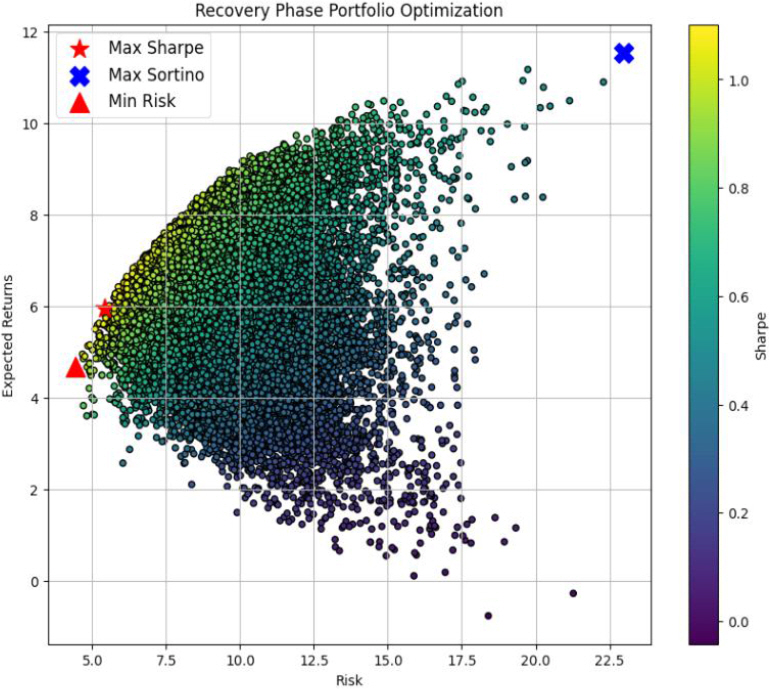
경기순환 주기의 각 상태인 호황기, 후퇴기, 침체기, 회복기별로 데이터를 모아서 해당 상태에 적합한 포트폴리오 최적화를 수행하였으며, 경기순환 주기에 맞는 포트폴리오의 최대 샤프 지수, 최대 소르티노 지수, 최소 리스크의 값은 Table 3과 같고, 경기순환 주기별 포트폴리오 최적화 그래프는 각각 호황기는 Figure 3, 후퇴기는 Figure 4, 침체기는 Figure 5, 회복기는 Figure 6과 같다. 각 경기순환 주기별 최적화 지수를 살펴보면 호황기에서는 최대 샤프 지수와 최대 소르티노 지수가 모두 높게 나타난다. 이는 상승기에는 수익을 추구하는 데 중점을 두는 것이 유리한 전략임을 시사한다. 또한, Min Risk는 0.664124로 상대적으로 낮은 값을 갖는다. 후퇴기에는 최대 소르티노 지수가 57.170240로 매우 높게 나타났다. 이는 하락기에는 리스크 관리와 안정성이 중요한 요소로 작용함을 나타내며, 소르티노 지수가 위험을 고려한 투자 전략에서 유리하다는 것을 보여준다. 침체기에는 최대 소르티노 지수가 2.094981로 상대적으로 높게 나타났다. 이는 불확실한 시기에는 소르티노 지수가 높아 위험을 적극적으로 고려한 투자 전략이 필요하다는 것을 강조한다. 회복기에는 최대 샤프 지수는 1.217564이고, 최대 소르티노 지수가 10.404536으로 둘 다 높게 나타났다. 이는 회복기에는 높은 수익을 추구하면서도 위험을 관리하는 데에도 성공할 수 있는 투자 전략이 가능함을 나타내며, 다양한 지수들이 상호 보완적으로 유리한 방향으로 작용하는 것을 알 수 있다(Table 3.).
4.2.2 DRL을 이용한 포트폴리오 최적화 결과
연구 기간의 80% 기간은 DRL 모델별로 학습을 하였으며 나머지 20%는 테스트 구간으로 모델별 성능측정을 하였다. 학습 기간의 포트폴리오 최적화 방법을 수행하는 강화학습을 하였으며, 모델별 하이퍼파라미터 튜닝은 하지 않았다. DRL을 이용한 포트폴리오 최적화 연구는 최대 샤프 지수를 학습하는 Sharpe DREAM, 최대 소르티노 지수를 학습하는 Sortino DREAM, 그리고, 경기 상승기에는 최대 샤프 지수를, 경기 하락기에는 최대 소르티노 지수를 학습하는 Sharpe-Sortino DREAM 의 세 가지 DRL 모델을 이용하였다. 실험 결과는 다음과 같다.
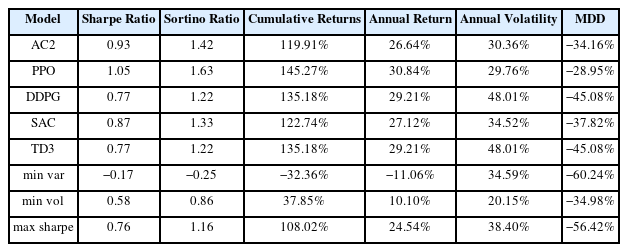
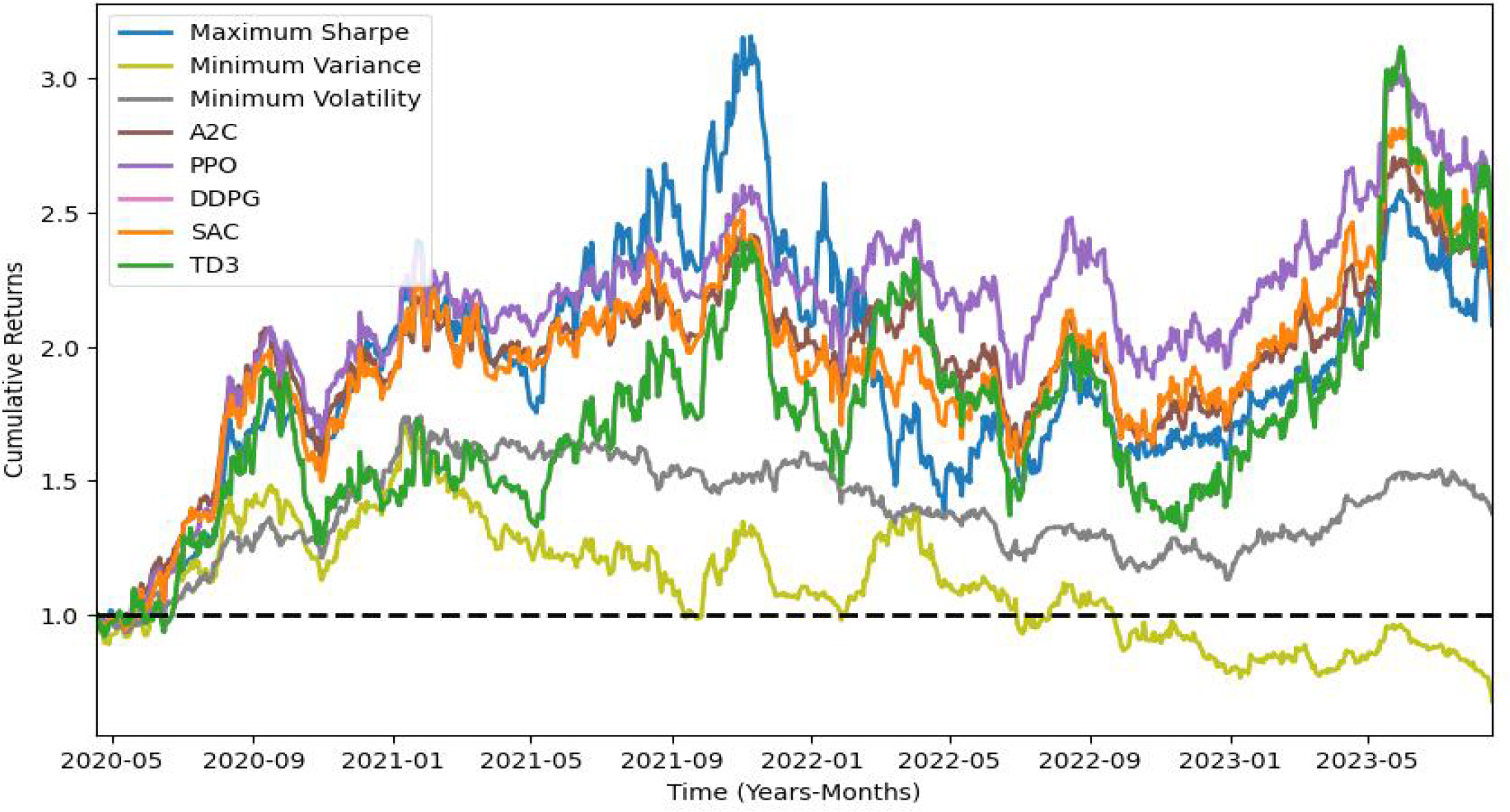
첫째, Sharpe DREAM의 성능 평가 결과는 Table 4와 같고 수익률 그래프는 Figure 7과 같다. 성능 평가 결과를 바탕으로 보면 PPO 모델이 1.05로 높은 수준의 샤프 지수를 기록하면서도, 연간 수익률과 누적 수익률 역시 상대적으로 가장 높은 결과를 기록하였다. 또한, DRL 모델인 AC2, DDPG, SAC, TD3 모델이 샤프 지수와 연수익률에서 max sharpe 모델의 샤프 지수 0.76과 Cumulative returns 108.02%보다 우수한 성과를 나타내고 있다.
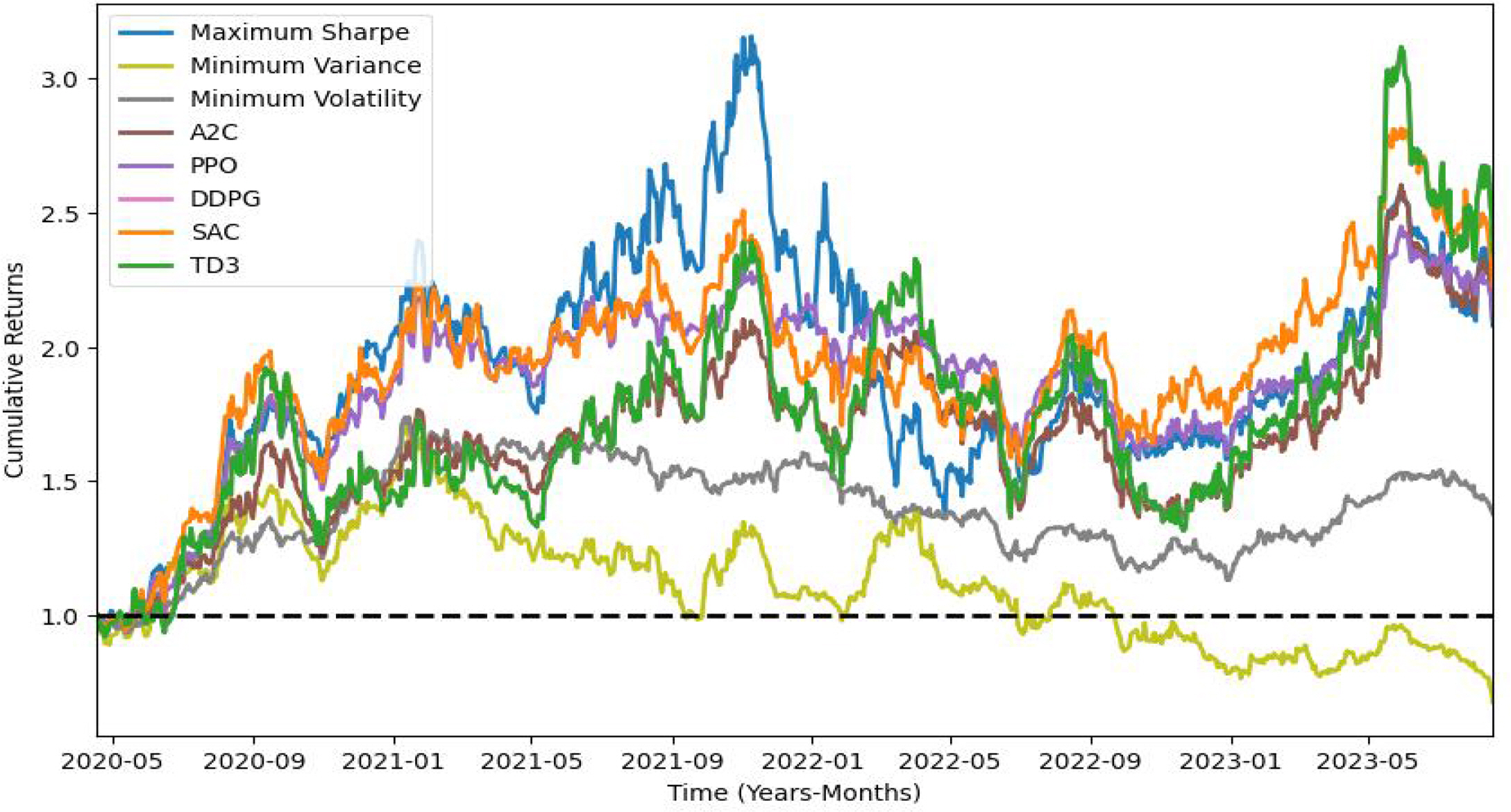
둘째, Sortino DREAM의 모델별 성능 평가 결과는 Table 5.와 같고 수익률 그래프는 Figure 8과 같다. 시험 결과를 검토하면, 소르티노 지수를 최대화하는 관점에서 볼 때 PPO 모델이 소르티노 지수가 1.52로 가장 우수한 성능을 보였다. 소르티노 지수는 하락한 수익률에 대한 리스크를 고려하는 지표로, 모멘텀이나 양의 기대수익률이 없는 상황에서도 높은 값을 가질 수 있다. 따라서 PPO 모델의 소르티노 지수가 1.52로 가장 높다는 것은 해당 모델이 하락한 수익률에 대한 리스크를 효과적으로 관리하면서 높은 수준의 수익률을 달성했다는 것을 의미한다. 이와 함께 PPO 모델은 누적 수익률 25.46% 와 연간 수익률 113.16%로 역시 상대적으로 좋은 결과를 보였다. 이에 따라 PPO 모델은 소르티노 지수를 최대화하는 관점에서 높은 성능을 나타낸다. 또한 TD3 모델과 DDPG 모델이 0.77로 높은 수준의 샤프 지수를 기록하면서도, 연간 수익률 29.21%와 누적 수익률 135.18% 로 역시 수익률 관점에서는 상대적으로 좋은 결과를 보여준다.
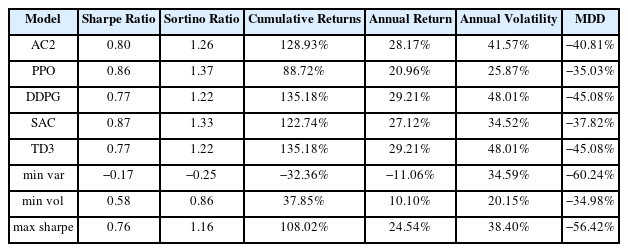
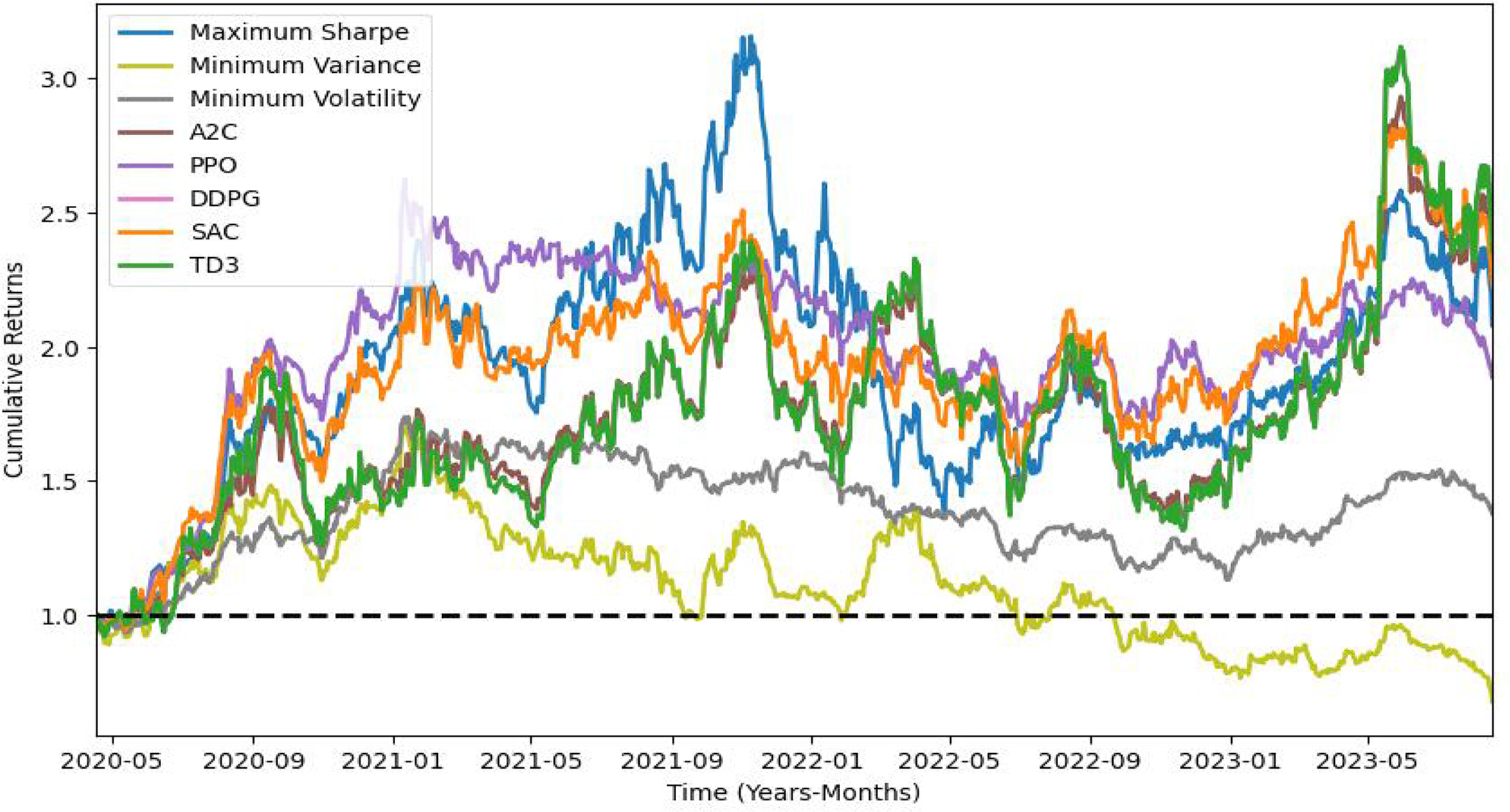
셋째, Sharpe-Sortino DREAM 성능 평가 결과는 Table 6과 같고 수익률 그래프는 Figure 9와 같다. 성능 평가 결과를 바탕으로 보면, SAC 모델이 샤프 지수가 0.87로 수익과 리스크를 동시에 추구하는 관점에서 가장 높은 성능을 보이며, 또한 TD3 모델과 DDPG 모델이 0.77로 높은 수준의 샤프 지수를 기록하면서도, 연간 수익률 29.21%와 누적 수익률 135.18%로 역시 상대적으로 좋은 결과를 보여준다.
실험 결과를 종합하면 다음과 같다. 첫째, 샤프 지수를 최대화하는 실험 결과에서는, Sharpe DREAM의 PPO모델이 1.05로 가장 높은 샤프 지수를 기록하였다. PPO 모델은 수익률 대비 리스크가 높은 샤프 지수를 가진다. Sortino DREAM 에서는 PPO 모델이 0.99 로, Sharpe-Sortino DREAM 에서는 SAC 모델이 0.87로 가장 높은 샤프 지수를 유지하고 있다. 둘째, Sortino Ratio를 최대화하는 관점에서는 Sortino DREAM 에서 PPO 모델이 가장 높은 소르티노 지수인 1.63을 기록하였다. 두 성능 평가에서도 PPO 모델이 높은 Sortino Ratio를 유지하고 있다. 셋째, Cumulative returns 관점에서는 Sharpe DREAM에서 PPO 모델이 가장 높은 누적 수익률을 기록한 145.27%를 보이고 있다. Sortino DREAM 과 Sharpe-Sortino DREAM에서는 DDPG 모델과 TD3 모델이 135.18%로 가장 높은 누적 수익률을 기록하였다. 마지막으로, MDD 관점에서는 Sharpe DREAM에서 MDD 측면에서는 PPO 모델이 -28.95%로 가장 낮은 손실을 보이고 있다. Sortino DREAM에서는 PPO 모델이 –30.57%로, Sharpe-Sortino DREAM에서는 minimum volatility 모델이 –34.98%로 가장 낮은 손실을 기록하였다.
5. 논의 및 결론
본 연구에서는 DRL 기반 경기순환 주기별 효율적 자산 배분 모델인 DREAM을 제안하였다. DREAM은 다양한 상황과 환경에서 최적의 포트폴리오를 구성하기 위한 세 가지 모델을 도입하였으며, 경기순환 주기에 따라 자산 배분을 최적화하는 데 큰 도움을 주었다. 실험 결과에서는 Sharpe DREAM은 PPO 모델이 145.27%, Sortino DREAM과 Sharp-Sortino DREAM은 DDPG 모델과 TD3 모델이 135.18%의 누적 수익률을 기록하였다.
본 연구는 선행연구와 다음과 같은 차이점이 있다. 첫째, DRL을 활용한 포트폴리오 최적화 모델은 과거 데이터에 의존하지 않고도 동적인 상황에 대응할 수 있으며, 이는 급격한 변동성이나 예측 불가능한 사건에 대응하기 어려운 기존의 통계 기반 연구의 한계를 극복하는 데 도움을 주었다. 둘째, 경기순환 주기를 고려한 최적의 포트폴리오 구성은 성과를 향상시킬 수 있는 잠재력을 제공하지만, 기존 연구에서는 이러한 최적화 모델을 제시하지 못한 점에서 차별화된다. 셋째, 우리는 DRL을 통해 최적의 포트폴리오를 구성하는 방법을 제안하였으며, 상황에 따라 적절한 보상 함수를 사용하여 포트폴리오의 성과를 민감하게 조절하고 최적화할 수 있다.
본 연구의 시사점은 DREAM 모델이 다양한 상황에서 안정적이며 수익성 있는 투자 전략을 제공한다는 점이다. 변동성보다는 수익을 추구하는 경우 Sharpe DREAM을, 변동성에 민감한 포트폴리오 구성을 위해서는 Sortino DREAM를 활용하는 것이 유리하며, 또한, 경기순환주기에 따라 샤프 지수와 소르티노 지수를 모두를 고려한 Sharpe-Sortino DREAM을 이용하여 장기적인 안정성과 수익을 추구할 수 있다.
본 연구의 한계점으로는 한정된 기간의 국내 주식 데이터를 사용하였으며, 다양한 데이터셋과 자산군 및 시장 상황에서 검증이 제한적이다, 또한, 강화학습 모델의 학습 과정에 따른 불안정성과 새로운 상황에 대한 대응력 부족이 있다. 따라서 향후 연구 방향으로는 더 다양한 데이터셋과 시장 상황에서 DREAM 모델의 성능을 검증하고 일반화하는 연구와 포트폴리오를 구성하는 자산의 동적 배분의 연구도 필요하다. 복잡한 DRL 모델의 특성으로 인한 상관분석이나, 해석 가능한 모델의 추가 연구가 필요하다. 또한, DRL 모델의 안정성을 향상하고 변동성 예측 및 리스크 관리를 개선하는 방안을 탐구하며, 금융 시장의 효율성과 안정성을 향상시키기 위한 다양한 DRL 기반 모델을 개발하고자 한다.