상관된 시계열 자료 모니터링을 위한 다변량 누적합 관리도
Multivariate CUSUM Chart to Monitor Correlated Multivariate Time-series Observations
Article information
Trans Abstract
Purpose
The purpose of this study is to propose a multivariate CUSUM control chart that can detect the out-of-control state fast while monitoring the cross- and auto- correlated multivariate time series data.
Methods
We first build models to estimate the observation data and calculate the corresponding residuals. After then, a multivariate CUSUM chart is applied to monitor the residuals instead of the original raw observation data. Vector Autoregression and Artificial Neural Net are selected for the modelling, and Separated-MCUSUM chart is selected for the monitoring. The suggested methods are tested under a number of experimental settings and the performances are compared with those of other existing methods.
Results
We find that Artificial Neural Net is more appropriate than Vector Autoregression for the modelling and show the combination of Separated-MCUSUM with Artificial Neural Net outperforms the other alternatives considered in this paper.
Conclusion
The suggested chart has many advantages. It can monitor the complicated multivariate data with cross- and auto- correlation, and detects the out-of-control state fast. Unlike other CUSUM charts finding their control limits by trial and error simulation, the suggested chart saves lots of time and effort by approximating its control limit mathematically. We expect that the suggested chart performs not only effectively but also efficiently for monitoring the process with complicated correlations and frequently-changed parameters.
1. 서론
시스템의 지속적 모니터링 및 이상 상태에 대한 신속 탐지는 시스템 운영 프로세스 관리에 있어 필수불가결한 과업이다. 다양한 형태의 이상 반응을 빠르고 정확하게 찾아낼수록 그로 인한 위험 및 피해를 최소화할 수 있기 때문이 다. 이로 인해 많은 통계 기법이 제조 시스템, 환경 관리 시스템, 전염성 질병 관리 시스템 등의 프로세스 관리를 위해 사용되어 왔다(Kim et al., 2019; Kim and Sohn, 2020; Seo and Yum, 2019). 가장 흔하게 사용되는 기법 중하나는 통계적 관리도로써, 대표적으로 슈하르트 관리도, 누적합(CUSUM) 관리도, 지수가중이동평균(EWMA) 관리도 등이 존재하며, 이후 이를 다변량 프로세스 모니터링을 위해 확장 시킨 T2 관리도, 다변량 누적합(MCUSUM; Multivariate CUSUM) 관리도, 다변량 지수가중이동평균(MEWMA; Multivariate EWMA) 관리도 또한 다양한 분야 에서 널리 사용되어 왔다. 단변량 프로세스 모니터링의 경우, Fricker et al.(2008)은 여러 환경조건에서 실험했을때 CUSUM 관리도가 슈하르트 관리도나 EWMA 관리도에 비해 프로세스의 미세한 변화를 탐지해내는 성능이 뛰어나다고 평가하였다. 다변량 프로세스 모니터링의 경우에는 현재 시점에서 얻은 관측치만을 반영하여 프로세스의 상태를 탐지하는 T2 관리도에 비해 이전 시점에서 얻어진 관측치와 현시점의 관측치를 모두 활용하는 MCUSUM 관리도와 MEWMA 관리도가 프로세스의 미세 변화 탐지에 있어 상대적으로 더 뛰어난 성능을 보인다(Montgomery, 2009).
한 번에 하나의 프로세스 품질특성치 정보만을 모니터링 할 수 있는 단변량 CUSUM 관리도에 비해 다변량 CUSUM 관리도는 여러 품질 특성치를 동시에 모니터링할 수 있다는 장점을 가지지만 기존의 다변량 관리도들은 대부분 각 품질특성치가 서로 독립이라는 가정 하에 고안된 것들이어서 관측되는 품질특성치들 사이에 자기 상관관계나 교차 상관관계가 존재하는 경우에는 그 탐지 성능을 그대로 유지 및 보장하기가 어렵다. Woodall and Ncube(1985)는 여러 개의 품질 특성치를 단변량 CUSUM 관리도를 통해 각기 따로 관리하기 보다는 하나의 MCUSUM 관리도를 이용하여 모든 특성치를 통합 관리하는 것이 프로세스의 이상 변동을 더 신속하게 탐지해내지만, 품질 특성치들 간에 교차상관관계가 강할 경우 그 탐지 성능이 저하될 수 있음을 보였다. 이러한 Woodall and Ncube(1985)의 MCUSUM 관리도의 단점을 보완하기 위해 Jiang et al.(2011)은 모니터링 하는 특성치들 사이에 교차 상관이 존재하여도 적용이 가능한 MCUSUM 관리도를 제시하였으나, 이 관리도는 시뮬레이션을 이용한 시행 착오를 통해 상황에 따른 관리 한계를 일일이 추정해야할 필요가 있어 상황변화가 심하거나 변량이 많은 경우에는 관리 한계 추정에 오랜 시간과 노력이 소모된다. 이후 Lee et al.(2014)는 Kim et al.(2007)의 단변량 CUSUM 관리도에 대한 관리 한계 추정식을 응용하여 일정 조건하에서는 시뮬레이션 대신 간단한 수치적 계산으로 MCUSUM 관리도의 관리한계를 추정 부여할 수 있는 SMCUSUM 관리도를 개발함으로써 관리도 사용을 위한 사전 준비 시간을 크게 단축시켰다.
한편, 자기상관관계를 가지는 프로세스 품질 특성치들을 모니터링하기 위해서는 모형 기반 MCUSUM 관리도가 널리 쓰여왔다. Noorossana and Vaghefi(2006)는 각 관측치를 예측하기 위해 수립한 단변량 시계열 모형으로부터 잔차를 계산하고, 자기 상관성이 배제된 이들 잔차를 모니터링하는 MCUSUM 관리도가 자기 상관성을 가지는 원래의 관측치 자료에 적용된 MCUSUM 관리도보다 이상상태 탐지 신속성 측면에서의 성능이 더 우수함을 보였다. 또한, Arkat et al.(2007)도 다변량 VAR(Vector Auto-regression) 시계열 모형과 ANN(Artificial neural net) 모형을 이용하여 얻은 잔차에 MCUSUM 관리도를 적용하는 것이 원래의 자료에 MCUSUM 관리도를 바로 적용하는 것에 비해 성능이 우수함을 보였다. 이 후에는 본격적으로 기계학습 모형 기반 관리도들이 도입되어, Issam과 Mohamad (2008)는 2차원 자료에 대해 ANN 모형과 SVR(support vector regression) 모형의 잔차에 기반한 관리도들을 VAR 모형의 잔차에 기반한 관리도와 비교하였고, 전자의 관리도가 후자보다 더 뛰어나다고 평가하였다. Kim et al. (2012)은 최대 10차원의 서로 다른 3가지 자기상관관계 수준을 가지는 다변량 자료를 토대로 한 9가지 시나리오를 가지고 다양한 잔차 기반 MCUSUM 관리도들의 성능을 비교하였다. 앞서 설명된 VAR, ANN, SVR 모형을 포함한 많은 모형에 대한 잔차 기반 MCUSUM 관리도들을 실험한 결과, Kim et al.(2012)은 ANN 모형의 잔차를 기반으로한 MCUSUM 관리도가 다양한 차원 수와 자기상관 정도를 다루는 데에 있어 타 관리도보다 상대적으로 우수한 성능을 보임을 확인하였다. 그러나 이러한 모든 잔차 기반 MCUSUM 관리도 역시 관리도의 실행에 있어 필수적으로 요구되는 관리한계 값의 추정을 위해 반드시 시뮬레이션을 통한 시행착오적 실험이 선행되어야만 한다는 전통적 MCUSUM 관리도의 단점을 그대로 지니고 있어, 관리도 실행 준비과정에서 많은 시간과 노력을 들여야만 한다.
이에 본 연구에서는 기존의 MCUSUM 관리도들이 가진 여러 단점들을 상호 보완할 수 있는 방법론을 소개하고그 성능을 기존의 여타 MCUSUM 관리도들과 비교 평가하고자 한다. 이어지는 본문의 2장에서는 먼저 다루고자 하는 문제에 대해 설명하고, 3장에서는 문제를 풀기 위한 새 방법론을 제안하며, 4장에서 방법론의 성능 평가를 위한 실험 진행 후, 5장에서 결론을 논한다.
2. 문제 배경
모니터링 시스템은 프로세스의 이상 상태 탐지를 위해 매 시점 t 에서 m개의 프로세스의 품질특성에 대한 관측치를 수집한다. 이 관측치들은 센서에 의해 짧은 간격으로 수집되는 것으로 자기 상관성 및 교차 상관성을 지닐 수있으며, 각 시점 t에서 수집되는 m개 변량에 대한 관측치는 벡터 Xt = (x1t, x2t, ..., xmt)' 로 표현된다. 프로세스에 이상 발생 시, Xt 의 평균 벡터 μ는 δx = (δx1, δx2,..., δxm) ' 만큼 변화하며 이 평균 변화량 벡터 δx 는 알려져 있거나 통계적으로 추정할 수 있다고 가정한다. 이러한 상황 하에서 우리는 프로세스에 이상 상태 발생 시 이 이상 상태를 최대한 신속하게 탐지하여 경고 알람을 울리는 것이 목표로 한다.
MCUSUM 관리도를 이용한 프로세스 모니터링 시, 관리도는 매 시점에 수집되는 Xt 들을 기반으로 관찰 통계량을 계산하고 해당 통계량이 정해진 관리한계 값을 넘어서는 시점에 이상 상태를 알리는 경보를 울린다. 따라서 이상상태가 발생하지 않았어도 언젠가는 오경보가 울릴 수 있고, 실제 이상상태가 발생했다 하더라도 그 이상 발생 시점과 경보가 울리는 시점에는 시차가 있을 수 있다. 이러한 관리도의 성질에 따라 관리도의 성능 평가는 ARL0 (In-control Average Run Length)과 ARL1 (Out-of-control Average Run Length)를 기반으로 이루어지는데, 이는 각각 ‘정상상태 하에서 오경보가 울릴 때까지 걸린 평균 시간’과 ‘실제 이상상태 발생 후 경보가 울리기까지 걸린 평균 시간’으로 설명된다. 따라서, ARL0 은 크고 ARL1 은 작은 관리도가 탐지 신속성 면에서 좋은 평가를 받는다. ARL0 과 ARL1 은 관리한계 값에 따라 달라질 수 있으므로, 일반적으로는 미리 정해둔 특정 ARL0 값을 달성할수 있는 관리한계를 시뮬레이션을 이용한 시행착오를 통해 찾아내고, 그 같은 관리한계 값 설정 하에서 얼마나 작은 ARL1 값을 달성하는가를 관리도 평가 지표로 삼는다.
3. 방법론
본 연구에서 제안하는 방법론의 전체적인 틀은 Figure 1과 같다. 방법론은 크게 두 단계로 나뉘어져 있는데, 첫 단계에서는 이전 관측치 자료들을 이용하여 정상상태에서의 Xt 를 예측하기 위한 모형을 만든다. 예측에는 여러 모형이 이용될 수 있지만, 본 방법론에서는 기존의 타 연구에서 비교적 좋은 결과를 내었던 VAR 모형과 ANN모형을 선택하였다. 모형을 통해 얻어진 t시점의 예측치
3.1 자료 모형화
본 연구에서는 정상 상태에서의 다변량 시계열 자료값을 예측하고 잔차를 계산하기 위해 각각 VAR 모형과 ANN 모형을 사용하였다. 사용된 각각의 모형에 대한 설명은 다음의 하위 장에서 찾아볼 수 있다.
3.1.1 VAR 모형
VAR 모형은 일변량 자기회귀모형을 다변량 자기회귀모형으로 확장시킨 것으로 다변량 시계열 예측에 활용될 수 있다. 만약 정상 상태의 프로세스의 관측치가 시차 p인 자기상관성을 가지고 있다면 아래의 VAR 모형으로 표현될 수 있다.
이 때, Ai는 시차 i = 1,2, ..., p에 해당하는 m × m 자기상관 계수 행렬로 보통 표본 자료를 통해 추정될 수 있다. ϵt는 서로 독립이며 동일 분포를 따르는 오차항 벡터로 평균이 0 벡터, 분산-공분산 행렬이 Σr 인 다변량 정규분포를 따르는 백색잡음으로 간주된다. (이 Σr는 알려져 있거나 표본 자료를 통해 충분히 유추할 수 있다고 가정한다.) 해당 모형에서 t시점의 예측치는
이며, 이에 따라 잔차는
3.1.2 ANN 모형
ANN 모형은 기계학습 방법 중 하나로, 생물학적 신경망에서 영감을 얻어 고안된 통계적 학습 알고리즘이다. ANN 모형은 일반적으로 입력층, 은닉층, 출력층으로 구성되어 있다. 각 층의 노드(node)는 가중치가 부여된 선으로 연결되고, 은닉층의 각 노드에서는 활성화 함수를 통하여 입력받은 값을 변환 출력하며, 이 때의 가중치는 목적 함수를 최적화하는 학습 알고리즘에 의해 결정된다. 본 논문에서 사용된 ANN 모형은 t시점 이전의 관측치들인 Xt-1, Xt-2, ..., Xt-p 를 입력값으로 받아 t시점의 다변량 시계열 예측치
3.2 프로세스 모니터링
프로세스 모니터링 단계에서는 (직접적인 프로세스 관측치 Xt 대신) 3.1장의 모형들로부터 얻어진 잔차 벡터 Rt에 SMCUSUM 관리도를 적용하여 모니터링을 실시한다. 다만, SMCUSUM 관리도는 표준화된 자료를 그 입력값으로 하고 있기 때문에 Rt = (r1t, r2t, ..., rmt)' 는 먼저 표준화된 잔차 벡터 Yt = (y1t, y2t, ..., ymt)' 로 변환될 필요가 있으며, 이에 따라 Σr 과 δr 역시 Yt 의 분산-공분산 행렬인 Σy 와 Yt 의 평균 변화량 δ y 로 각각 변환될 필요가 있는데 이는 다음의 식 (4), (5), (6)에 따라 계산될 수 있다.
이 후 SMCUSUM 관리도의 관찰통계량 St 은 다음의 식 (7)과 (8)을 이용하여 설정되며, 해당 관찰통계량이 미리 설정된 관리한계 값을 넘어서는 시점에 프로세스 변화를 감지하는 경보가 울리게 된다.
k는 흔히 MCUSUM 관리도의 참고값으로 불리는 값으로 식(8)에서는
시뮬레이션을 이용한 시행착오를 통해 (목표로 삼는 ARL0 을 달성할 수 있도록 하는) 관리한계 값을 찾는 기존의 관리도들과는 달리, SMCUSUM 관리도의 관리한계 값 H는 다음의 수리적 계산식에 의해 추정된다.
Kim et al. (2007)과 Lee et al. (2013)의 연구를 바탕으로 하는 위 식 (9)에서
4. 실험 결과
모든 관측치 자료는 VAR 모형에 기반한 시뮬레이션을 통해 생성되었으며, 이를 통해 교차 상관 및 자기 상관을 가지는 2차원, 5차원, 10차원의 다변량 자료 모니터링에 대한 각 관리도의 ARL1 성능 평가가 이루어졌다. 실험은 i) 비교대상이 되는 각 관리도 별로 정상상태에서 목표 ARL0 을 달성하기 위한 관리한계 값을 우선 탐색한 후, ii) 해당 관리한계 값을 적용했을 때 이상상태에서 평균적으로 얼마나 빨리 경보를 울리는지(ARL1)를 측정하는 방식으로 수행되었다. 모든 차원에서 ARL 들은 같은 환경설정 하의 실험을 1000번 반복 진행한 후 얻어진 값의 평균으로 계산되었다.
4.1 2차원 실험 결과
2차원 상에서의 실험은 Arkat et al.(2007)의 설정과 동일하게 p = 1,
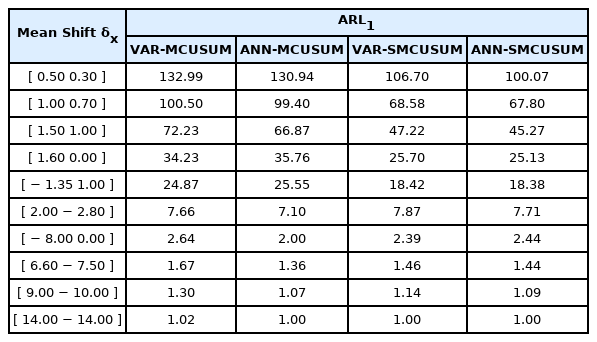
Table 1에 나타난 총 10개의 시나리오 중 평균 변화폭이 상대적으로 작은 상위 5개의 시나리오에서 SMCUSUM 을 이용한 관리도들이 기본 MCUSUM을 이용한 타 관리도들 대비 확연히 낮은 ARL1 을 달성하였음을 확인할 수 있다. 반면, 평균 변화폭이 상대적으로 큰 하위 5개의 시나리오에서는 SMCUSUM을 이용한 관리도가 타 관리도 대비 비슷하거나 미미하게 더 큰 ARL1 값을 가지는데, 이 들은 모두 k값이 상대적으로 큰 시나리오들로 SMCUSUM 관리도의 성능 저하에 영향을 받았기 때문인 것으로 판단된다.
2차원 실험에서 VAR-SMCUSUM과 ANN-SMCUSUM의 ARL1 값들이 크게 차이나지는 않았으나, 대부분의 경우 ANN-SMCUSUM이 VAR-SMCUSUM보다 낮은 ARL1 을 달성하였다.
4.2 5차원 실험 결과
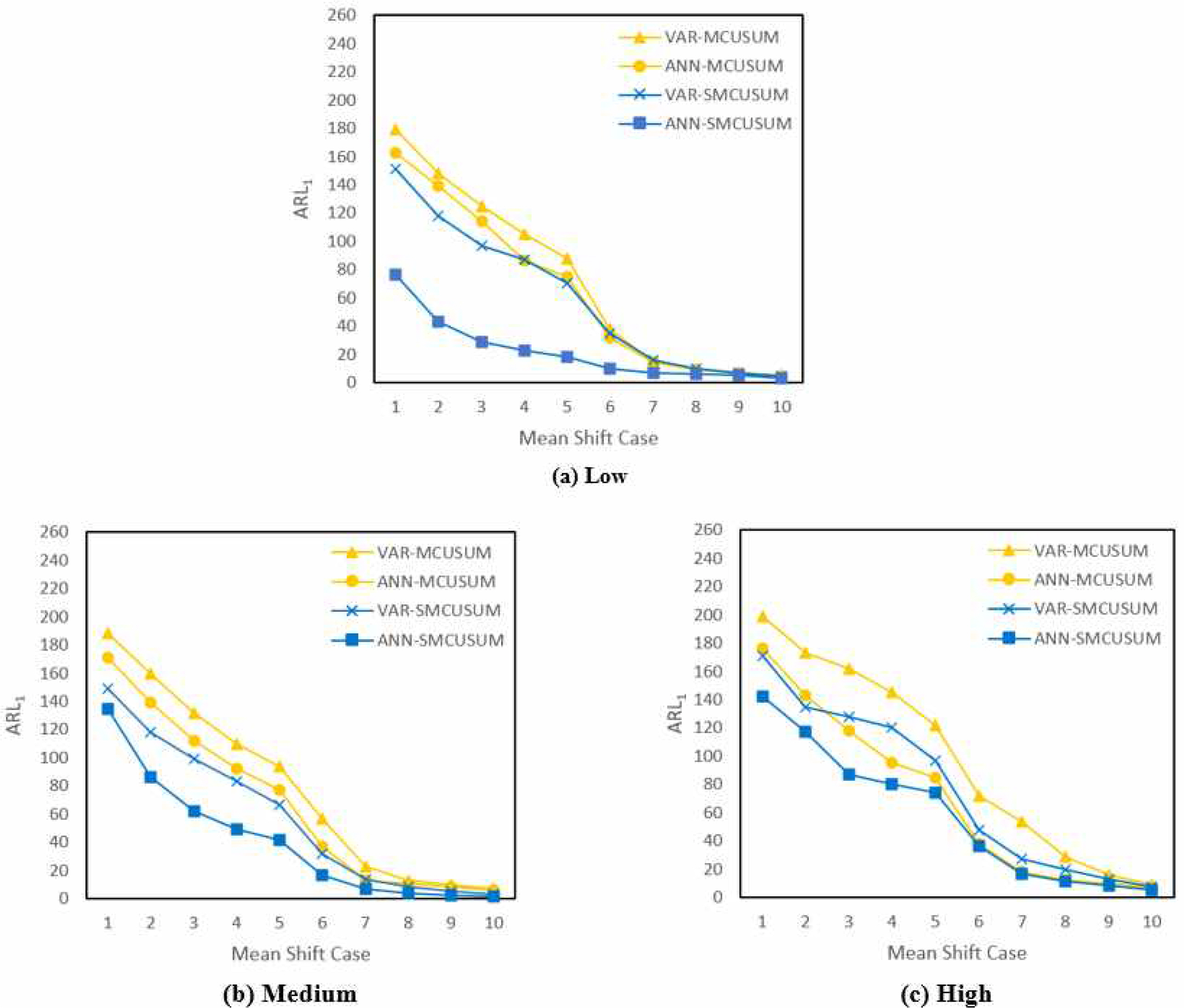
5차원 상에서는 Kim et al. (2012)과 동일하게 세 가지 서로 다른 자기 상관 수준(낮음, 중간, 높음)을 가지는 자료에 대해 Table 2의 두 번째 열에 표시된 서로 다른 10개의 5차원 δx 을 적용하여 실험을 수행하고, 그에 따른 ARL1 결과를 기록하였다. (p = 1, μ = 0, ARL0 = 200으로 설정되었으며, 그 밖의 A1 과 Σr 등에 대한 자세한 정보는 Kim et al. (2012)의 부록을 참고하라.) 각 비교 대상 관리도에 대한 ARL1 결과는 Figure 2에서 찾아볼수 있으며, Figure 2의 (a), (b), (c)는 각기 낮은, 중간의, 높은 자기 상관 수준을 가지는 자료를 가정하였을 때의 실험 결과를 나타낸다. 거의 모든 경우에서 VAR 모형을 이용한 관리도보다는 ANN 모형을 이용한 관리도가 더 뛰어난 성능을 보였는데 이는 Kim et al. (2012)의 결과와 일견 일치한다. 5차원 실험에 있어서도 MCUSUM 관리도보다는 SMCUSUM을 이용할 때 전반적으로 더 낮은 ARL1 을 달성하였으며, 특히 ANN-SMCUSUM 관리도가 타 관리도 대비 우수한 ARL1 성능을 보였다. 이상상태에서의 자료 평균 변화폭이 상대적으로 작은 경우(Table 2의 1~5번 경우)에는 ANN-SMCUSUM 관리도의 성능 차이가 더욱 뚜렷이 나타난다.
4.3 10차원 실험 결과
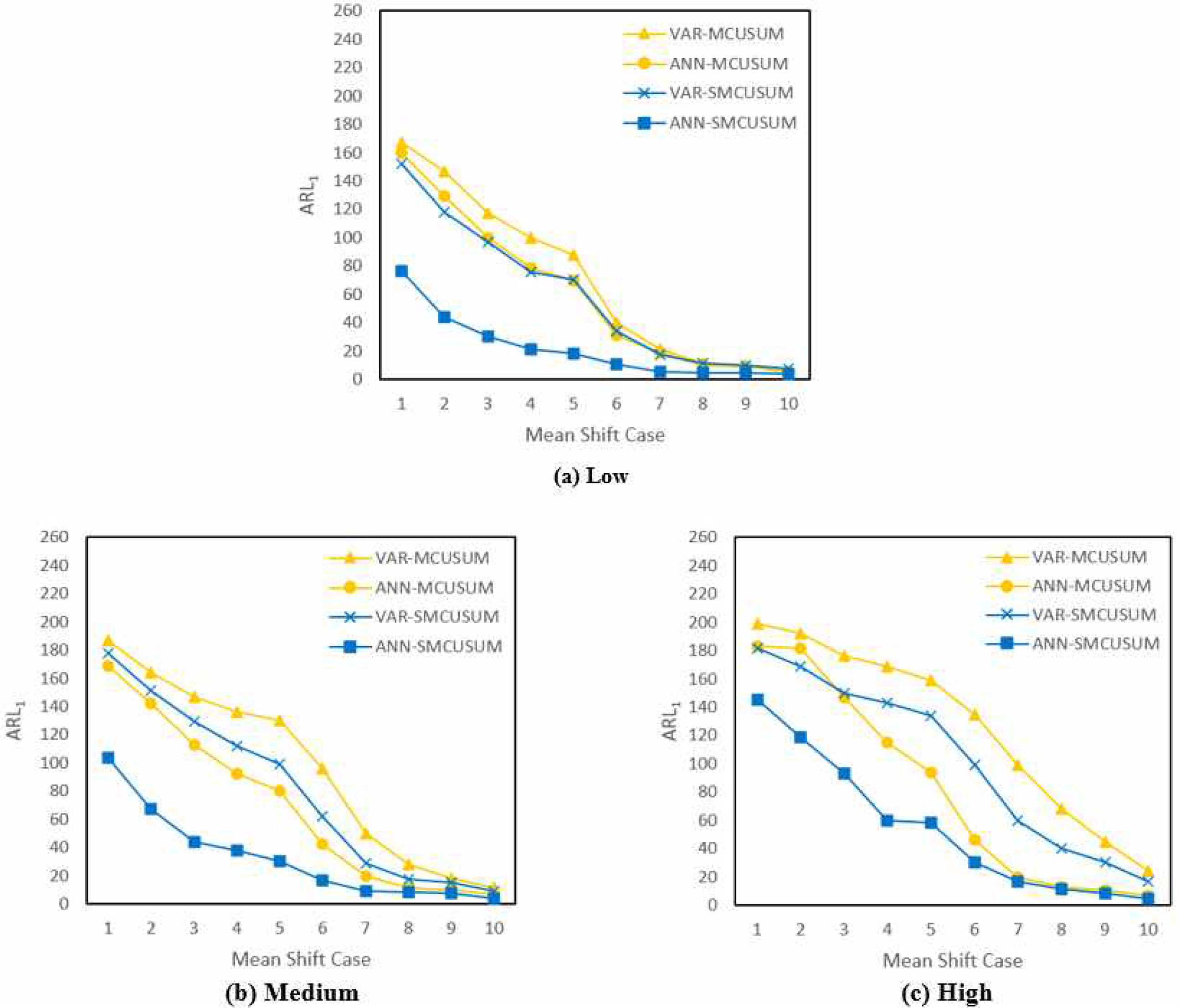
10차원 상의 실험 역시 5차원 실험과 마찬가지로 Kim et al. (2012)과 동일한 환경설정 아래 이루어졌으며, 세가지 서로 다른 자기 상관 수준을 가지는 자료에 대해 Table 2의 세번째 열에 나타난 10개의 10차원 δx 을 적용한 후 ARL1 결과를 관측하였다. 각 비교 대상 관리도에 대한 ARL1 결과는 Figure 3에서 찾아볼 수 있다. 10차원 상에서도 전반적으로 VAR 모형을 이용한 관리도보다는 ANN 모형을 이용한 관리도가 더 뛰어난 성능을 보였으며, VAR과 ANN이용 시의 성능 차이가 5차원에서의 실험에서 보다 더 뚜렷이 나타났다. 또한 거의 모든 경우에 있어 MCUSUM 관리도보다는 SMCUSUM을 이용할 때 더 우수한 탐지 성능을 보이며, ANN-SMCUSUM 관리도가 타관리도 대비 낮은 ARL1 을 달성함을 다시 한번 확인할 수 있다.
5. 결론
본 연구에서는 다변량 시계열 관측치의 미세 변화를 신속하게 탐지할 수 있는 잔차 기반 SMCUSUM 관리도를 제안하였다. 여러 환경 조건 하에서 이루어진 많은 실험을 통해 우리는 VAR 모형 보다는 ANN 모형의 잔차에 기반한 관리도가, 기존의 MCUSUM을 이용한 관리도보다는 SMCUSUM을 이용한 관리도가 ARL1 측면에 있어 상대적으로 더 뛰어나며, 특히나 ANN 모형의 잔차에 SMCUSUM을 적용한 관리도는 비교 대상으로 선택된 다른 관리도들 대비 그 성능이 우수함을 확인하였다. 기존의 다른 MCUSUM 관리도들이 가진 단점을 상호 보완할 수 있도록 구성된 이 관리도는 프로세스에서 관측되는 다변량 시계열 데이터가 자기 상관 및 교차 상관을 모두 가지는 경우에도 적용할 수 있으며, 다양한 주변 상황에 맞추어 관리한계를 수리적으로 추정함으로써 관리도 실행을 위한 준비 시간을 크게 단축시킬 수 있어, 환경 변화가 심하고 관계가 복잡하게 얽혀있는 다변량 프로세스 모니터링 시 더욱 효율적이고 효과적으로 사용될 수 있을 것으로 생각된다.