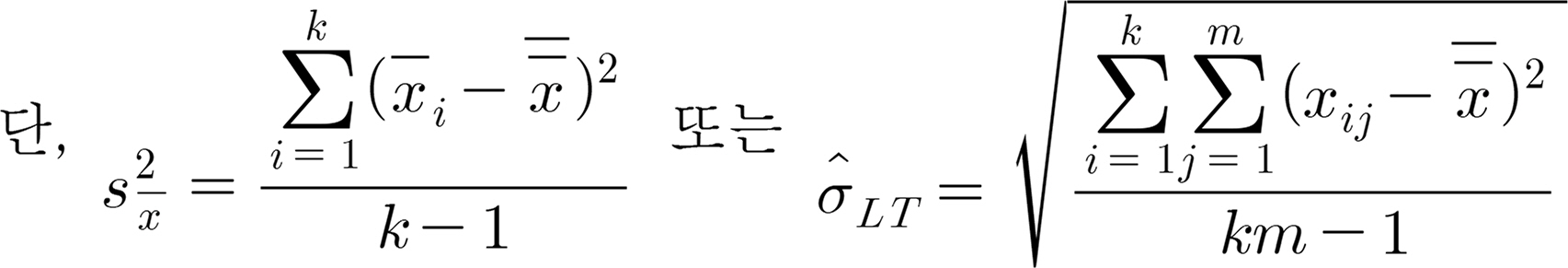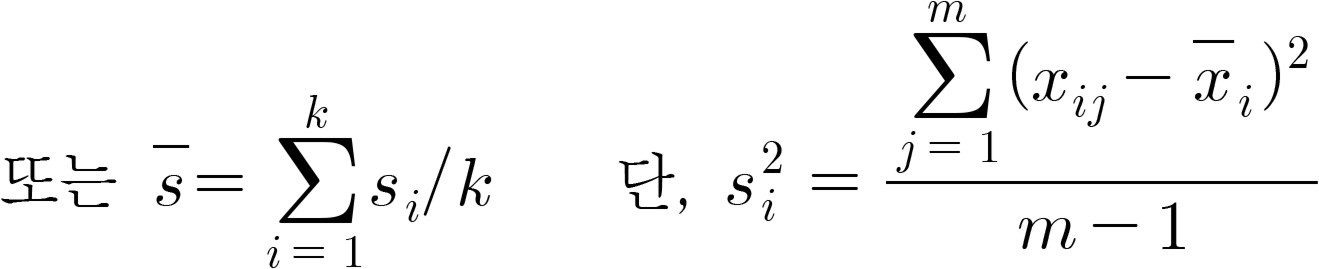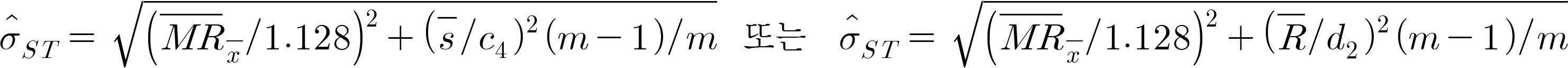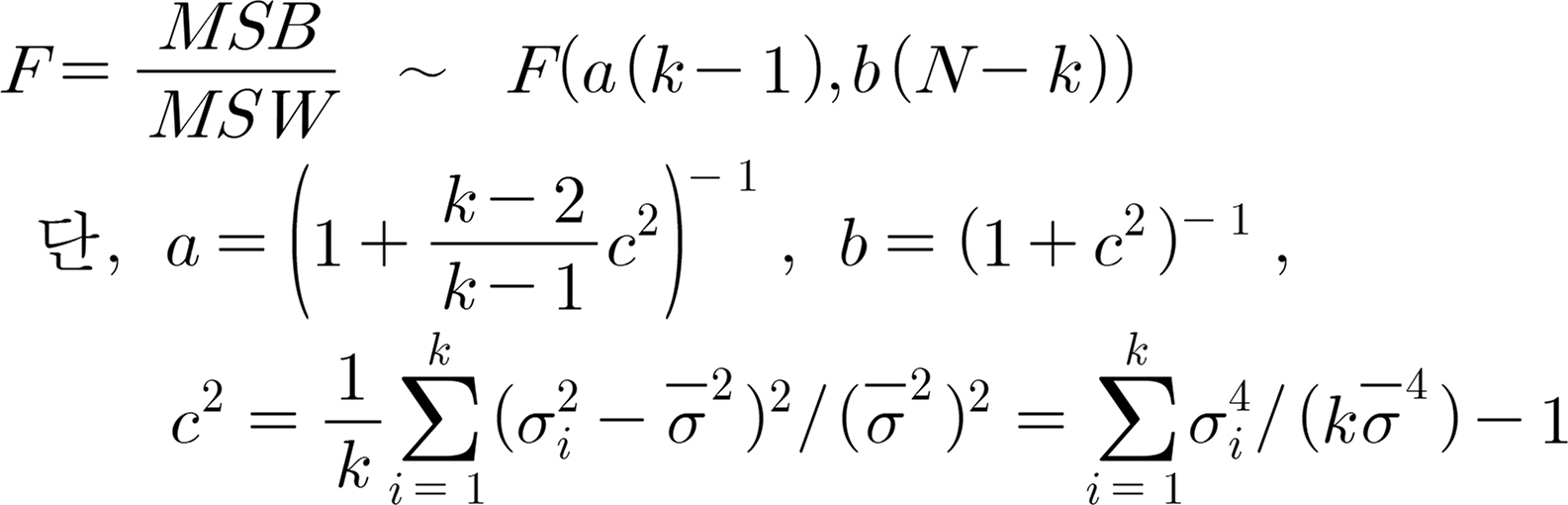1. 서 론
공정 모니터링은 유효한 통계 및 과학적 방법을 사용하여 변동을 식별하고 그 원인을 추적하여 이를 최소화하는 것을 목적으로 삼는다. 어느 정도 규모가 되는 기업들은 여러 제품을 생산하는 다수의 제조 시설을 글로벌하게 보유하고 있어, 전 세계적으로 엄청난 양의 공정 모니터링 데이터를 획득하고 있다. 따라서 공정 모니터링 시스템에는 제품별로 서너 개부터 수백 개까지 되는 공정 파라미터와 성능척도에 관한 능동적인 모니터링이 포함될 수 있다.
공정 모니터링에서 적절한 관리도의 선택은 보통 계수(이산) 또는 계량(연속)으로 대별되는 데이터의 유형에 의해 정해지는데, 계수형 데이터에 대해서는 p, ,np, u, c 관리도가, 계량 데이터에 대해서는 X ¯ - R , X ¯ - s
이런 관리도를 통해 공정의 통계적 관리(statistical control) 상태 여부를 판정할 수 있다. 즉, 이상 원인을 제거하고 우연원인만 존재하는 통계적 관리상태가 되면 공정의 특성인 평균과 표준편차는 어느 정도 일정하게 되어 안정적(stable)이 되므로 공정 양태의 예측이 가능하지만(predictable), 공정이 안정적이더라도 항상 적합품을 생산하는 것은 아니다.
따라서, 공정이 안정적이라고 파악이 되면 공정능력이 충분한지(capable)를 조사해야 한다. 공정능력은 공정의 규격 부합도를 평가하는데, 공정능력이 충분하지 못한 이유로는 공정변동이 규격폭에 비해 상대적으로 크거나 공정평균이 규격중심을 벗어나는(off-center) 경우를 들 수 있다.
Wheeler(2004)는 이런 점을 반영하기 위해 공정능력 수준과 통계적 관리상태를 각각 두 가지로 대별한 네 가지 상태로 구분하여, 공정의 기초상태를 파악하고 선제적인 통계적 공정관리(SPC)를 수행할 수 있는 방안을 제시하였다.
최근 들어 통계적 관리상태와 연관되는 척도로 안정성 비율(stability ratio; SR)과 안정성 척도(stability index; SI) 등이 제안되어 공정능력 척도와 연관시킨 새로운 공정관리 방법을 주장하고 있다(Sall, 2018; Jensen et al., 2019; White et al., 2021).
안정성 비율(SR)을 비롯한 안정성 척도(SI)는 1989년 Podolski(1989-90)가 최초로 제시한 이후 Cruthis and Riden(1992-93), Ramirez and Runger(2006) 등이 장.단기 공정의 변화를 보다 정확하게 파악하기 위해 여러 가지 통계량을 활용하여 검정할 수 있는 다양한 방법들을 제안하고 있는데, 먼저 이들의 특성을 2장에서 살펴본다. 3장에서는 기존의 안정성 척도의 약점을 보완한 새로운 안정성 척도를 제시하고 이들의 통계적 특성과 활용 방법을 다루고자 한다. 4장에서는 공정의 안정성과 공정능력을 동시에 고려하는 공정성능 그래프(process performance graph)를 소개하고 개선된 그래프를 제시한다. 또한, 공정에서 접할 수 있는 파라미터의 여러 가지 상황에 따라 공정성능 그래프에 쓰이는 안정성 척도에 의한 공정 건전성(process health)의 판별 기준을 관리도 유형과 부분군의 크기 및 수에 따라 구한 후에 이의 활용방법을 예시한다. 마지막 장에서는 본 연구의 성과와 후속 연구가 필요한 주제를 제안한다.
2. 공정 안정성 척도에 대한 선행연구
공정 안정성 척도 중에서 안정성 비율(SR)은 장기 공정분산 추정값(long-term variance estimator : σ ^ 2 L T σ ^ 2 S T
으로 정의되며, Podolski(1989-90), Cruthis and Riden(1992-93), Ramirez and Runger(2006), Britt et al.(2016) 등이 채택하고 있다. Jensen et al.(2019)은 공정능력지수(process capability index; PCI)와 함께 사용하기 위해 안정성 비율(SR)의 제곱근인 안정성 척도(SI)
를 제시하였으며, Shper and Adler(2017)는 공정의 안정성을 파악하기 위한 척도로 이의 역수인 σ ^ 2 S T / σ ^ 2 L T
공정 안정성 척도는 단계 1(phase 1, 관리한계를 설정하는 해석용 관리도)와 단계 2(phase 2, 공정 모니터링 용도의 관리용 관리도)에 모두 사용될 수 있지만, 전자의 역할이 보다 중요하며, 공정 안정성 파악에 따른 유용성이 높으므로 본 논문에서는 특별한 언급이 없으면 단계 1의 상황을 고려한다. 단계 1에서 적용되는 계량형 관리도에 따라 장단기 공정산포의 추정법이 달라지므로 먼저 널리 활용되는 세 가지 관리도를 살펴본다. 여기서 k는 단계 1에 해당되는 부분군 수, mi는 부분군 i의 표본크기, 총 표본크기인 N = ∑ i = 1 k m i
(i) I-MR(X-Rm) 관리도: 각 부분군에서 mi=1인 경우
(ii) X ¯ - R
(iii) X ¯ - s
공정 안정성 척도에 관한 기존 연구들에서 채택된 장기와 단기 공정산포의 추정값과 적용한 통계량 분포를 기준으로 정리하면 다음과 같다.
장기 공정산포: 식 (3)/식 (5)
단기 공정산포: 식 (4)/식 (7)
통계량 F = σ ^ 2 L T σ ^ 2 S T
장기 공정산포: 식 (3)/식 (5)
단기 공정산포: 식 (4)/식 (7)
통계량 F = σ ^ 2 L T σ ^ 2 S T
장기 공정산포: 식 (3)/식 (6)/식 (8)
단기 공정산포: 식 (4)/식 (7)/식 (9)
통계량 분포: F = σ ^ 2 L T σ ^ 2 S T X ¯ - R
(iv) Gauri(2010)
장기 공정산포: 식 (3)
단기 공정산포: 식 (4)
시뮬레이션 수치실험으로 랜덤, 이동(shift), 추세(rend), 주기(cyclic), 체계적(systematic) 패턴 하에서 이전의 여러 방법을 비교하고 상당히 복잡한 형태를 가진 공정 안정성 지수(process stability indicator; PSI)를 제안하였지만, PSI가 특히 주기 패턴일 때 효율적이지 못하지만 안정성 비율(SR)은 그렇지 않다고 보고하고 있다. 또한, Wooluru et al.(2015)도 특히 N ≥ 32일 때 안정성 비율(SR)이 보다 유용하다고 추천하고 있다.
장기 공정산포: 식 (3)
단기 공정산포: 식 (4)(단, d2가 빠진 값을 채택함)
새로운 통계량S I ' = M R ¯ σ ^ L T
(vi) vJensen et al.(2019)
장기 공정산포: 식 (3)/식 (6)/식 (8)
단기 공정산포: 식 (4)/식 (7)/식 (9)
통계량 S I = σ ^ L T σ ^ S T
테이블1에 기존 주요 연구문헌에 대한 내용이 요약되어 있다. 또한, 기존 연구들의 추정 및 검정 과정은 통계패키지 JMP 13 ~ 16에 반영되고 있으며, 부분군간 평균이 다를 경우(예를 들어 batch 생산)는 다음과 같이 부분군 간의 평균에 관한 M R ¯ x ¯
그러나 식 (4)에서 M R ¯ M R ¯
그리고 White et al.(2020)는 공정건전성을 평가하기 위해 SI를 포함한 여러 관련 지표와 이를 활용하는 구체적 지침을 제안하였으며, 측정시스템까지 포함하는 지표를 추천하였다. 이 논문에서는 공정안정성을 주 대상으로 다루고 있으므로 측정시스템의 평가지표까지는 고려하지 않는다.
한편 식 (10)은 X ¯ - s
3. 새로운 공정 안정성 척도
3.1. 모형
본 논문에서는 각 군에서 하나의 관측값이 존재할 경우는 이전의 연구자들이 추천한 방법을 그대로 사용할 수 있으므로 제외하며, 각 군에 다수의 관측값이 있는 경우가 전자보다 널리 활용되고 있으므로(Montgomery, 2013), 이 상황에 한정한다.
군별로 공정평균과 분산이 변할 경우에 i번째 군의 j번째 관측값 xij에 관한 일반적인 모형은
로 나타낼 수 있으며, 그리고 군별로 표본크기가 일정하다면(N=km),
가 된다. 식 (11)에서 ANOVA의 기본 모형과 달리 각 군의 분산이 일정하지 않을 수 있다는 확장된 모형으로 가정하고 있다.
새로운 안정성 비율을 식 (6)과 (7), 식 (8)과 (9)보다 식 (6)과 (9)로부터 다음과 같이 정의하면
이므로, 만약 각 군의 평균과 분산이 동일하다면, SR은 F분포가 포함된 다음의 식 (14) 형태로 표시할 수 있으나, 각 군의 평균과 분산이 상이할 때는 별도의 근사 방법을 적용하여야 한다.
(14)
이로부터 SR은 공정능력지수(process capability index, PPI, Ppk) 및 공정성능지수(process performance index; PCI, Cpk)와 다음 관계가 성립한다.
여기서 S S W = ∑ i = 1 k ∑ j = 1 m ( x i j - x ¯ i ) 2 = ∑ i = 1 k ∑ j = 1 m ( ϵ i j ϵ ¯ i ) 2 E ( S S W ) = ∑ i = 1 k ( m - 1 ) σ i 2
이 되어 MSW의 기댓값은 각 부분군의 분산들의 평균이 된다.
그리고 SSB의 기댓값은
이 되며, α ¯ = 0
이므로 MSB의 기댓값은
가 된다. 따라서 식 (16)과 (17)에서 보듯이 MSB와 MSW는 독립이나 F분포를 따르지 않으므로 다음 소절에서 언급한 바와 같이 별도의 근사방법이 필요하다.
한편, 각 군의 표본크기가 다를 경우는 m을 mi로 바꾸고 식 (11)에서 ∑ i = 1 k m i α i = 0 ∑ i = 1 k ( m i - 1 ) = N - k . α ¯ = ∑ i = 1 k m i α i / N = 0
여기서 σ ¯ 2
3.2 공정 평균과 분산이 변할 경우의 근사분포
공정이 안정될 경우라도 공정산포가 일정하지 않고 어느 정도의 변화 범위를 허용할 수 있다. 이런 경우 표본크기가 동일한 경우는 대체적으로 F 검정이 강건(robust)하다고 알려져 있다. 하지만 표본크기가 어느 정도 크거나 분산비(가장 큰 분산과 작은 분산의 비)가 얼마나 되어야 F 검정을 충분히 사용 가능한지에 대한 연구결과가 연구자별로 상이한 편이고, 또한 강건하지 않다고 주장하는 연구도 여러개가 있다(Blanca et al., 2018).
여기서는 관리도 적용 상황인 표본크기가 10이하인 경우가 주 대상이 되므로, 분산이 동일하지 않으면서 소표본일 경우에 F 검정의 대안으로 추천될 수 있으면서(Parras-Frutos, 2013), 보다 수월하게 본 문제 상황에 적용할 수 있는 검정법은 Brown-Forsythe(1974) 방법이다. 이 방법은 특정한 경우에 제1종 오류를 증대시킬 수 있으므로, 본 논문에서는 Box(1954)의 방법을 이용해 자유도의 근사 정확도를 향상시킨 수정 Brown-Forsythe 방법을 채택한다.
먼저 N=mk일 때 σ ^ S T
(20)
여기서, ν 2 = [ ∑ i = 1 k w i 2 / ( m - 1 ) ] - 1 , w i = σ i 2 ∑ j = 1 k σ j 2 = σ i 2 k σ ¯ 2 , σ i 2 = E ( s i 2 )
Box(1954)는 H0 : α1=⋯=αk=0(단, 분산이 다를 경우)일 때 E ( M S B ) = E ( M S W ) = σ ¯ 2
여기서 c는 σ2에 관한 변동계수 형태에 속한다. Brown-Forsythe(1974) 방법에서 분모의 자유도는 b(N-k)=k(m-1)/(1+c2)=v2가 되어 위와 같아지지만, 분자의 자유도는 모든 표본분산이 동일할 때인 k-1이 된다. 따라서 이 방법에 의한 임계값은 실제보다 작아져, 제1종 오류는 명목값을 초과하게 된다.
이런 점을 고려하여 Mehrotra(1997)에 의해 제안된 수정 Brown-Forsythe 방법은 분모의 자유도는 위와 동일하지만 분자의 자유도는 Box(1954)의 식 (21)로부터 다음과 같이 근사하고 있으므로, 본 논문에서는 몬테카를로 시뮬레이션 대신에 해석적인 이 방식을 채택한다.
4. 공정성능 그래프의 활용
4.1 공정성능 그래프
Wheeler(2004)는 관리도의 관리상태와 공정능력 충족 여부를 기준으로 네 가지 영역으로 대별하여 각 영역별 필요 조치들을 적시하고, 이를 통해 공정특성들의 기초 상태를 파악하여 SPC를 수행하는 방안을 제시하였다. 최근 들어 Wheeler의 아이디어를 구체화시키면서, 상당 개수의 공정특성이 있을 경우 효율적으로 선별하기 위한 방법으로 공정 안정성과 공정성능 척도에 관한 이차원 도표인 공정성능 그래프가 추천되고 있다(Sall, 2018; Ramirez, 2018; Jensen et al., 2019; White et al., 2021).
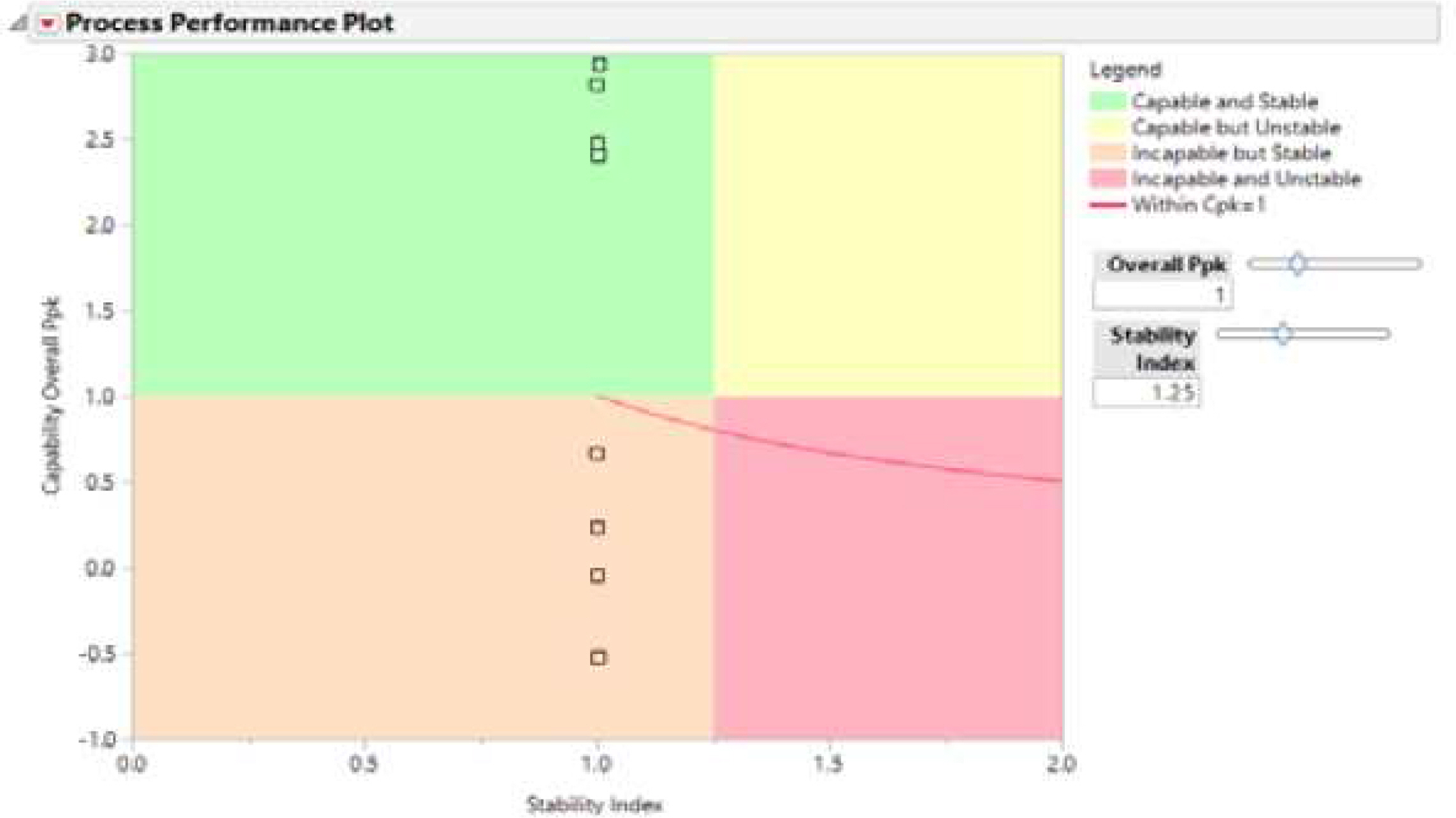
Figure 1은 JMP에서 제공하는 공정성능 그래프 화면으로 수평축은 안정성 척도(SI)를, 수직축은 공정성능지수(process performance index; PPI, Ppk)를 표시하는 2차원 영역으로, 전자는 1.25, 후자는 1.33을 기준으로 네 가지 영역으로 구분하고 타점된 공정특성의 상태에 대한 선별을 쉽게 할 수 있도록 구성되어 있다. 또한 이 그림에서 공정능력지수(process capability index; PCI, Cpk)의 상태도 일부분 곡선 형태로 보여 주고 있다. 한편 White et al.(2021)은 이 그림에 Cp와 목표값 이탈지수(target index)까지 색깔과 점 크기로 표시하고 있는데, 규격중심이 이 값과 일치하는 보편적 상황일 때 Ppk 및 Cpk에 반영되고, 증가된 정보제공량에 비해 공정상태 분별력이 떨어질 수 있어 그리 유용성이 높지 않다고 판단된다.
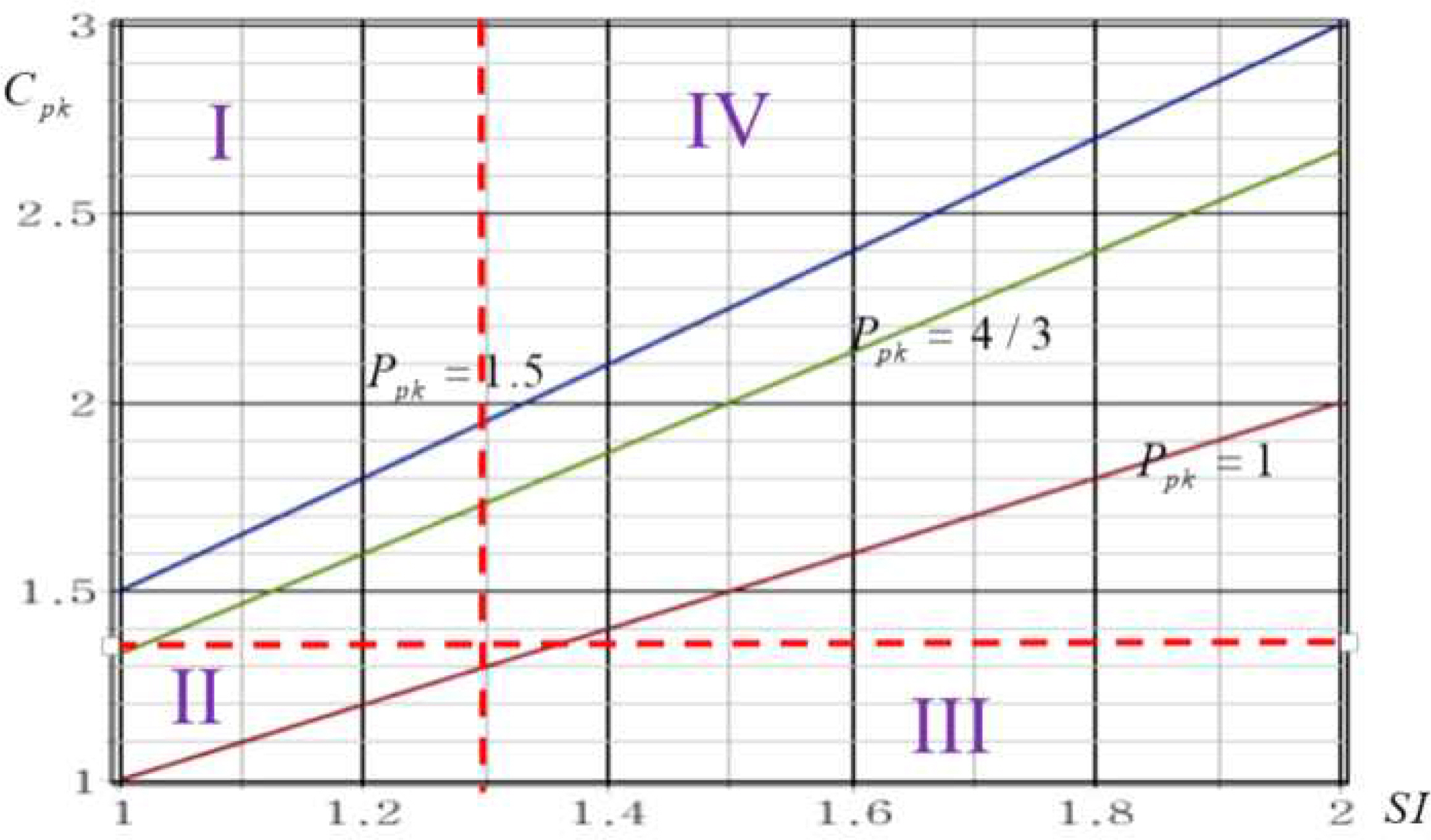
식스 시그마에서 도입된 공정성능지수 Ppk는 공정이 안정적이라고 전제되어야 공정능력을 평가할 수 있다는 SPC의 기본 개념과 어긋나 추천하지 않는 학자와 전문가도 제법 많은 편이다(Montgomery, 2013). 따라서 본 논문에서는 Figure 2에 표시된 바와 같이 식 (15)와 같은 제곱 형태인 SR보다는 이의 제곱근인 SI를 채택하고, 수직축 Ppk대신에 Cpk를 표시하는 수정된 공정안정성 평가 그래프를 제안하며, 또한 Ppk에 관한 정보도 추가하므로서 더 많은 정보를 이용하여 공정 안정성을 평가하도록 하였다.
그리고 안정적인 공정으로 간주하는 안정성 척도(SI)가 1.25(SR은 1.252)이어야 한다는 근거도 명확하지 않으며, 또한 Britt et al.(2016)은 공정 안정성 척도로 SR을 채택하여 1.252=1.5625가 아닌 1.5을 기준으로 채택하는 등 공정안정성에 대한 정확한 기준이 없으므로, 본 논문에서는 이 기준이 타당한지를 검토하기 위해 앞 절에서 제안된 통계량과 근사분포를 이용하여 단계 1의 여러 여건에 따른 SR의 임계값을 구하고자 한다.
만약 SR의 임계값이 설정되면 이로부터 구한 SI및 Cpk(대체적으로 1.33)에 따라 Figure 2처럼 공정성능 그래프를 네 가지 영역으로 구분하며, 영역 I에 타점된 공정특성은 이상적 상태에 근접한 경우이므로 시정조치가 요구되지 않지만, 영역 II일 때는 Cpk가 낮은 원인(즉, 공정평균의 중심/목표값 이탈 정도, 산포(표준편차)의 과대 문제, 규격의 적정성 등)을 조사해야 한다. 그리고 영역 IV일 때는 공정의 안정성에 저해되는 요인을 조사하여 조치를 취한 후에 Cpk가 높은 이유가 규격의 폭이 넓게 설정되어 있는지를 확인할 필요가 있다. 마지막으로 영역 III에 해당되는 공정은 먼저 공정 안정성을 저해하는 원인에 대한 시정조치를 취한 후에 공정능력을 높일 방법을 찾아야 한다.
4.2 평균과 산포 변동을 고려한 SR 임계값 산출
공정 안정성 평가 시에 어느 정도의 공정 평균의 이동(drift)과 공정산포의 변화(주로 증대)를 허용할 수 있다. 일례로 식스 시그마에서는 장기적으로 공정평균이 공정 표준편차의 1.5배 정도 이동하는 것을 용인하여 이를 공정능력 평가 시에 반영하고 있다.
본 논문에서는 이런 여건을 반영하여 공정 평균과 산포의 변화를 모두 허용하지 않을 경우, 둘 중에서 한 가지만 허용할 경우의 두 가지와 더불어 공정 평균과 산포의 변화를 모두 허용할 경우 등 네 가지 상황으로 구분하여 안정성 지수의 임계값을 구하고자 한다.
여기서 F분포의 유의수준으로 0.01를 택했는데, 0.05나 0.0027(관리도)를 택할 경우도 동일한 방법으로 구할 수 있으며, 여기서는 중간 값에 해당되는 0.01만 수록하였다.
그리고 부분군 수 m은 X ¯ - R X ¯ - s X ¯ - R X ¯ - R R ¯
먼저 Table 2에는 공정평균과 산포가 동일하고 일정한 경우 앞 3장 1절의 식 (14)를 이용하여 부분군의 수 및 크기에 따른 임계치가 수록되어 있다.
그리고 Table 3에는 공정산포는 일정하지만 공정평균에 어느 정도 변화를 감내할 수 있는 경우로 △ = μmax-μmin(즉, 평균이탈(off-mean)이 최대 △/2)가 1.0일 때의 부분군의 수에 따른 임계치가 수록되어 있다. 여기서 μi들의 평균이 μ가 되도록 설정하면서 가장 극한적인 경우로, k가 모두 짝수일 때 k/2개 군의 공정평균이 μmin이고 k/2개 군의 공정평균이 μmax 일 경우로 상정하였다.
그런데 식 (14)의 분자에 포함된 MSB의 기댓값은 식 (17)이 되지만, 제안된 SR에 적용되는 F분포의 분위수는 이로부터 구할 수 없다. 즉, 비중심 모수가 m ∑ i = 1 k α i 2 / σ 2 = N △ 2 / 4
여기서, Fα와 F α ' f 1 = ( ν 1 + δ ) 2 ν 1 + 2 δ
공정산포가 변할 경우로 분산범위가 σ2 ∼ dσ2, d > 1일 경우를 상정하자. 식 (21)에서 0 ≤ c2 ≤ k-1인데, c2의 최댓값은 한 값이 dσ2이고 나머지 k-1개가 σ2일 때가 되며, 그 값은 (k-1)(d-1)2/(d-1+k)2=(k-1)[(d-1)/(d-1+k)]2이다. 따라서 이 경우를 대입하여 식 (21) 및 (22)에 의해 k에 따른 임계치를 구한 결과가 Table 4에 정리되어 있다.
실험계획 교재 등에서도 분산비가 3정도 되어도 기존의 ANOVA 검정을 적용할 수 있다고 기술하고 있으므로 (Dean and Voss, 1999), 여기서는 이를 약간 초과한 4(표준편차의 비로 2)인 경우를 대상으로 설정하였다.
마지막으로 공정평균과 공정산포가 모두 변할 경우는 위의 두 경우의 SR 임계값 도출방법을 결합하여 얻은 결과가 Table 5에서 볼 수 있다. 여기서 각 부분군의 표준편차가 다를 수 있으므로 △를 1.0σmin일 때로 설정하였다.
(1) k와 m이 증가함에 따라 임계값은 당연히 감소하고 있다.
(2) X ¯ - R
(3) 공정평균의 이동 허용여부가 공정분산의 변화보다 큰 영향을 미침을 알 수 있다.
(4) 공정평균의 이동과 분산의 변화를 허용하지 않거나 공정분산의 증대(4배까지)만 허용할 경우는 단계 1의 부분군의 수의 범위(20 ~ 100)일 때 JMP의 기준 1.252=1.5625보다 더 엄격해야 함을 보여 주고 있다.
(5) 공정평균의 이동만을 허용할 경우(± 0.5σ)는 단계 1의 부분군의 수일 때(즉, k가 20~30) 대체적으로 판별기준을 1.5 ~ 1.6 정도로 삼을 수 있다.
(6) 공정평균의 이동과 분산을 모두 허용할 경우는 단계 1의 부분군의 수가 40이상 정도 되어야 판별기준으로 1.5 ~ 1.6으로 삼을 수 있다.
4.3 수치예제
첫째 자료는 자동차 부품 공장의 공정 1의 공정특성 데이터((원래값-목표값)*1,000)이며, 둘째 자료는 같은 공장의 공정 2의 공정특성 데이터로서 기본정보와 이로부터 계산된 여러 가지 요약값 및 SR과 SI값이 Table 6에 정리되어 있다.
SR을 식 (14)로 구한 결과를 공정 1에 대해 예시하면 다음과 같이 1.046이 되며,
Cpk=min((50-1.113)/(3·10.07)=1.62, (1.113+50)/(3·10.07)=1.66)=1.62 이다. 참고로, 공정 1에 관한 X ¯ - R
공정성능 그래프에 두 공정의 SR의 제곱근인 SI와 Cpk를 타점한 결과를 Figure 4에서 볼 수 있는데, 두 공정 모두 공정산포의 증대만을 허용할 경우(Table 4에서 공정 1은 1.19 = 1.09 1.11 = 1.05 1.63 = 1.28
5. 결론
최근 들어 관리도에 의해 판정하는 통계적 관리상태와 연관되는 척도로 안정성 비율과 안정성 지수 등이 제안되고 있다. 더불어 이와 공정능력 척도를 반영한 2차원 공정성능 그래프를 통해 다수의 공정특성에 관한 두 가지 척도를 타점하여 공정의 건전성에 관한 기초상태를 판별함으로써, 우선적으로 어떤 조치들을 취해야 할지를 파악할 수 있는 방법이 소개되고 있다.
공정의 안정성에 관한 척도로 Podolski(1989)가 최초로 장기와 단기 공정분산의 추정값에 관한 비로 정의된 안정성 비율을 제시한 이후 여러 가지가 제안되고 있는데, 본 논문에서는 이들의 특성을 살펴본 후에 이들을 개선할 수 있는 새로운 안정성 척도 공식을 제안하였다. 그리고 이의 통계적 특성을 조사하여 F분포의 자유도를 근사하는 등의 구체적인 활용방법을 제안하였다.
그리고 공정특성의 대표적 모수인 평균과 산포(분산)의 변동 허용정도에 관한 여러 가지 상황에 따라 공정성능 그래프에 쓰이는 안정성 척도에 의한 판별 기준을 부분군의 수와 크기, 적용 관리도 형태로 구분하여 도출하는 해석적인 방법론을 제시하였다. 그리고 기존의 공정성능 그래프를 일부 개선하고 이의 사용법을 구체적으로 예시하였다.
따라서 기존 연구에서 채택하고 있는 부분군의 수와 크기와 무관하게 안정성 척도에 관한 임계값을 적용하는 방식은 추천하기 힘들며, 대상 공정에서 가장 작은 부분군 수를 가지는 경우를 보수적인 기준으로 삼거나, 공정별로 부분군 수의 적정범위를 지정하고 이에 적합한 임계값을 3장에서 제안된 방법을 이용하여 설정하고 운용하는 것이 공정안정성 판정에 관한 위험도를 줄일 수 있다. 기존 연구내용에 대한 본 논문을 비교분석한 내용을 Table 7에 요약하였다.
본 논문에서는 제안된 공정 안정성 비율에 관한 임계값을 정확하게 구할 수 없는 경우에 근사적으로 구한 자유도를 이용하고 있는데, 향후에 이의 근사 정확도를 몬테카를로 시뮬레이션 등을 통해 광범위하게 조사할 필요가 있다. 그리고 공정능력을 판정하는 공정능력지수의 보편화된 판별기준인 1.33처럼 JMP의 1.252을 포함하여 공정 안정성 비율에 관한 보편적 판별기준을 찾는 연구도 하나의 주제가 될 수 있을 것이다.