 |
 |
AbstractPurposeCompared to the rapid growth rate of the domestic automotive LED industry so far, the predictive analysis method for demand forecasting or market outlook was insufficient. Accordingly, product characteristics are analyzed through the life trend of LEDs for automotive exterior lamps and the relative strengths of p and q using the Bass model. Also, future demands are predicted.
MethodsWe used sales data of a leading company in domestic market of automotive LEDs. Considering the autocorrelation error term of this data, parameters m, p, and q were estimated through the modified estimation method of OLS and the NLS(Nonlinear Least Squares) method, and the optimal method was selected by comparing prediction error performance such as RMSE. Future annual demands and cumulative demands were predicted through the growth curve obtained from Bass-NLS model. In addition, various nonlinear growth curve models were applied to the data to compare the Bass-NLS model with potential market demand, and an optimal model was derived.
ResultsFrom the analysis, the parameter estimation results by Bass-NLS obtained m=1338.13, p=0.0026, q=0.3003. If the current trend continues, domestic automotive LED market is predicted to reach its maximum peak in 2021 and the maximum demand is $102.23M. Potential market demand was $1338.13M. In the nonlinear growth curve model analysis, the Gompertz model was selected as the optimal model, and the potential market size was $2864.018M.
1. 서 론자동차 산업은 100년이상 시장이 지속되고 있는 핵심산업 중 하나로, 최근에는 전자 및 ICT 소프트웨어 기술이 접목되어 더욱 확장 및 발전을 거듭하고 있다. 이제 자동차는 내연기관으로 대표되는 기계 중심에서 전기모터, 배터리, 각종 센서, LIDAR/RADAR/카메라 등에 의한 자율주행기술, 최신 CAN 통신, LED(Light Emitting Diode)Headlamp 광학기술 등 전자 및 소프트웨어 중심으로 혁신적으로 진화하고 있다.
자동차의 눈에 해당하는 헤드램프에서 주 광원으로 LED가 국내에 처음 적용된 시점은 2009년 에쿠스 리무진에 채택되었을 때이다(박종원, 2012). 물론, 그 이전부터 자동차에 센터페시아(Center fascia), 변속레버 PRND, 보조제동램프(CHMSL, Center High Mount Stop Lamp) 등에 제한적으로 LED가 적용되었다. 그러나, 본격적으로 자동차용 LED 시장 성장을 이끈 부품들은 헤드램프, 후미램프, 방향지시램프 등 자동차 외장(exterior) 관련 제품들이며, 이 중 헤드램프를 제외하고 대부분 2000년대 초반을 기점으로 삼는다. 자동차용 LED 시장의 비약적 성장 원인은 대략 다음과 같다. 첫째, 자동차 램프에 LED 적용 이후, 소비자들의 차량구매 선택에서 중요한 요소 중 하나인 디자인에서 획기적인 변화를 가져왔기 때문이다. 작은 사이즈의 기구적 강점을 가진 LED는 헤드램프 등 디자인 설계자유도를 높인다. 자동차 이미지는 헤드램프 디자인에 상당부분 결정되며, 부분변경 모델(Facelift)에서도 변화가 추진되어 타 부품 대비 제품 사이클이 2배 짧아졌다(임은영, 2018). 둘째, 최근 자동차 램프는 과거처럼 단순 물체 식별 기능을 넘어 반도체, ICT 기술과 결합하여 지능형, 능동형으로 발전하는 고부가가치 기술이 되고 있는데, 이에 사용되는 핵심 부품이 LED이기 때문이다. 예로, 기존 운전자 중심에서 벗어나 보행자, 상대편 차량의 안전을 고려하여 대상 객체의 위치에 따라 자동으로 빛을 선택적으로 조사시키는 ADB (Adaptive Driving Beam), AADB(Advanced ADB)는 여러 개의 고효율 LED들로 구성되어 있다(HMG 저널, 2018).
셋째, 안전 및 환경규제도 자동차 LED 수요성장 가속화 요인으로 지목된다. 안전규제는 주간주행등(DRL, Daytime Running Light)과 보조제동등(CHMSL)이 대표적이며, 주간주행등은 낮 시간 교통사고 방지를 위한 조명장치로 2012년에 의무화되었고, 보조제동등은 후미차에 제동상황 인지를 높이고 연쇄충돌을 예방하기 위한 조명장치로 2008년에 의무화되었다. 또한, 환경규제 측면에서 LED는 기존 할로겐 램프 대비 1/3 수준의 에너지를 소모하고, 차량용 램프에서 발생되는 이산화탄소 절감효과가 큰 것으로 알려져 있다. 이와 같은 이유 등으로 자동차 LED 수요 및 시장규모는 더욱 성장하고 있는 것이다. 그러나, 이처럼 국내 자동차 램프와 차량용 LED 산업의 급격한 성장속도와는 달리 수요예측 또는 시장 전망 예측 분석은 그 중요도에 비해 깊이 있는 연구가 수행되지 않았고, 신뢰할 만한 수요예측방법도 소개되지 않았다. 더구나, 최근 LED를 포함한 차량용 반도체 공급부족(shortage) 현상이 심각한 수준에 이른 것은 정확한 수요예측에 실패함으로써 공급계획에 차질을 빚은 것도 여러 원인 중 하나로 지목되고 있기도 하다.
본 연구에서는 국내 자동차 외장 램프시장에서 시장점유율이 가장 높은 해외 제조사의 LED 매출데이터를 기반으로 Bass 확산 모형을 적용하여 수요예측과 제품 수명 트렌드 등 분석을 진행하였다. 먼저, Bass 확산 모형에서 모수추정방법 중 OLS의 수정된 추정법과 NLS 방법을 비교하여 적합한 예측 모형을 선택하였고, 여기서 추정된 모수를 통해 혁신계수(p)와 모방계수(q)의 상대적 강도 등 제품 특성 및 파생수치 등을 분석하였다. 또한, 잠재적 시장규모 m의 초기값을 통해 여러 가지 비선형 성장곡선모형에 적용하여 가장 적합한 모형을 도출하여 앞서 구한 Bass 확산 모형과 비교 분석하였다.
2. BASS 확산 모형(Bass Diffusion Model)2.1 모형의 이론적 배경확산모형은 제품의 수명주기(제품구매)를 혁신자(Innovator)와 모방자(Imitator) 요인으로 해석하며, 각 요인에 따라 다른 확산모형을 설명한다. 혁신자 요인에 의한 확산모형은 누적매출 Yt가 지수곡선 형태의 Yt=m[1-exp(-pt)]를 따르는 전제로, 시점 t 에서의 당기매출을 St=p(m-Yt-1)으로 모형화한 것이고(Fourt & Woodlock, 1960), 모방자 요인 확산모형은 누적매출 Yt가 로지스틱 곡선의
여기서 p는 혁신계수(0≤p≤1)로서 다른 사람의 구매 의사결정과 무관한 자발적 구매가 일어나는 것으로 기업 광고, 판촉 등 외적 변수에 의한 영향을 의미하고, q는 모방계수(0≤q≤1이며 기존 제품을 구매한 사람들의 평가나 경험에 의한 구전효과 영향을 의미한다. m은 제품의 잠재적 구매자 수이고, Yt-1은 t-1 시점까지의 누적매출이다. Bass 모형은 지수곡선과 로지스틱 곡선의 결합된 형태로써, Bass 모형에서 p가 0에 가까우면 로지스틱 곡선 모형이 되고, q가 0에 가까우면 지수곡선 모형이 된다. 혁신자와 모방자의 첫 구매에 대한 결합비율은
위의 확산모형을 바탕으로 성장곡선을 얻기 위해 식 (2-1)은 다음과 같이 바꿀 수 있다.
판매량 St는 누적매출의 증가율로 바꿔 표현할 수 있고, 다음과 같은 미분방정식 형태로 표현된다
여기서, 계수 a, b, c는 다음과 같다.
식 (2-3)을 풀면 누적매출과 당기매출에 대한 식은 다음과 같다.
또한, 당기매출 증가율이 최대가 되는 시점(t1)과 당기매출의 최대가 되는 시점(t2)은 아래와 같다(홍정식 외, 2012).
2.2 OLS에 의한 모수 추정법위 식 (2-2)에서, 당기매출 St와 누적매출 Yt에 대한 자료로부터, 혁신계수(Innovation coefficient) p, 모방계수(Imitation coefficient) q, 그리고, 궁극적 매출의 잠재적 최대값(Potential number of ultimate adopters) m을 추정한다.
식 (2-8)의 계수 a, b, c를 구하는 과정에서 선형회귀분석과 같이 OLS(Ordinary Least Squares) 방법을 이용하여 계수 a, b, c를 추정한 후, 이들과 모수 p, q, m과의 관계로부터, 모수 p, q, m의 추정치를 구한다.
2.3 자기상관 오차항을 고려한 추정법위의 전통적인 OLS 방법은 대부분의 연구에서 이산 시계열 데이터를 사용하고, 오차항은 일시적으로 상관관계가 없는 것을 가정으로 한다. 그러나, 이러한 접근 방식은 초기 단계에서 매출을 과대평가하고 피크 이후 매출을 과소평가시키는 등 심각한 시간 간격 편향을 발생시키는 문제를 가지고 있다. 잔차 사이에 상관관계가 존재할 때 OLS와 같은 확산모델의 선형화된 방법으로 추정 시 편향된 추정치뿐만 아니라 일관되지 않은 추정치를 얻을 수 있으므로, 다음과 같이 자기상관 오차항을 고려한 수정된 모델을 적용하여 추정한다.
여기서 ϵt가 차수(Order) h의 자기회귀과정일 때,
식 (2-9)의 오른쪽 두 번째 항은 과거 기간에 발생한 오차를 나타내며, 수정된 모델은 가중치 매개변수 ϕt에 의해 현재 시점의 오차를 수정한다(차경천 외, 2009).
2.4 NLS에 의한 모수 추정법NLS(Nonlinear Least Square) 방법은 추정된 모형과 실제 데이터의 오차 제곱합을 최소로 하는 다차원 비선형 모수 추정법이다. 앞의 OLS에 의한 모수 추정법 등 보다 NLS에 의한 추정법이 더 우수한 것으로 알려져 있다(Srinivasan and Mason, 1986). OLS는 비교적 쉽게 모수를 추정하는 장점이 있으나, Bass 모형을 이산적 시점 모형으로 변환하여 추정함으로써 모수추정에 편의(bias)가 발생하고 데이터가 peak time(수요의 최고점)을 포함하지 않을 경우 통계적으로 유의미한 결과를 얻기 힘들거나 잘못된 부호의 결과를 얻을 단점이 있다. 또한, p, q, m 등 모수는 직접 추정이 아닌 식 (2-8)과 같이 계수 a, b, c에 의한 간접 추정방식이다. 이에 반해, NLS 방법은 연속적 시점의 모형을 이용하여 p, q, m 등 모수를 직접 추정하는 장점이 있다. 즉, f(t)=(p+qF(t))(1-F(t))의 식을 미분방정식으로 풀면 누적확률분포함수(cdf: Cumulative Distribution Function) F(t)는 아래와 같다. 여기서, f(t)는 위 식 (2-1)의 m을 제외한 형태와 같다(하영욱 외, 1999).
식 (2-10)에 m을 취해주면 이것은 식 (2-4)와 같은 누적매출에 대한 식이 되고, 비선형 최소제곱법(Nonlinear MSE)에서 모수 p, q, m은 목적함수
3. 성장곡선 모형(Growth Curve Model)계량경제학 및 의/공학 등 다양한 분야에서 적용중인 성장곡선 모형은 대체로 S자 형태의 비선형 곡선과 잠재적 구매자 수 m값에 수렴하는 특성을 갖고 현실 상황을 아주 가깝게 표현하므로, 수요예측 방법으로 매우 유용하게 활용되고 있다. 이것은 초기에 잠재시장 일부만 시장에서 채택되고 시간에 따라 수요자들이 비선형적으로 증가하여 결국 잠재시장의 포화점에 이르게 되는 시장의 일반적인 상황을 잘 표현하기 때문이다(이군희 외, 2002).
예전부터 선행연구들에서 대표적으로 변형지수 곡선(Modified Exponential Curve), 로지스틱 곡선(Simple Logistic Curve), 곰페르츠 곡선(Gompertz Curve) 모형 그리고 Bass 확산 모형 등을 사용하여 왔고, 특히, 실제 산업 및 제품시장 수요예측 연구들에서 이들 4가지 성장곡선 모형이 자주 다루어졌다. 제한된 모수를 가진 모형으로 시장현상을 완벽하게 설명하는 것은 어렵지만 서로 이질적인 시장상황 또는 제품특징 등이 존재하는 현실에서 위의 4가지 모형들은 다음과 같은 차별적 특징으로 분석데이터에 대해 수요예측 모형의 적합성, 성장요인과 제품시장 특징 등은 어떠한지 구분하고 유추해 볼 수 있기 때문으로 생각된다. 이들 4가지 모형들을 간단히 구분하면 첫째, 혁신자 등 외부효과만을 고려한 변형지수 곡선, 둘째, 모방자 등 내부효과만을 고려한 로지스틱 곡선, 셋째, 로지스틱 곡선과 달리 변곡점 중심의 비대칭 S자 형태로 실제 시장을 잘 표현한다는 곰페르츠 곡선 모형이 있고, 마지막으로 본 논문의 주제인 Bass 확산모형의 성장곡선은 앞에서와 같이, 혁신자와 모방자 모두를 고려한 모형이고, S곡선의 변곡점 중심으로 좌우 비대칭 형태를 갖고 있다. 이외 세부적인 특징 비교는 이군희 외(2002), 홍정식 외(2012), 박도형 외(2014) 등의 선행연구들을 토대로 Table 1과 같이 정리하였다.
이를 바탕으로 자동차 외장 램프 LED 시장은 Bass 확산모형 분석과 더불어 수요예측에 있어, 어떤 성장곡선 모형에 가장 적합한지 그리고 어떤 성장요인과 시장성장 특징을 갖는 제품인지 등을 살펴보고자 하였다.
4. 자료 및 주요 방법론본 연구에 사용된 자료는 2006~2021년간 국내 자동차 램프 시장에 LED를 공급하는 해외업체의 LED 매출데이터이다. 이 LED는 2006년 자동차 램프 중, CHMSL에 처음 진입하여 매출을 시작하였다. 이 자료에는 일부 비자동차용 LED 매출도 포함되었으나, 전체적으로 차량용 LED 매출자료로 보아도 될 만큼 미미한 수준이며, 국내 자동차 외장 램프 LED 시장 점유율은 50% 이상으로 사실상 국내 시장 전체 매출을 대표한다고 볼 수 있다. 참고로, 제품수량 보다 매출을 변수로 한 것은 LED는 다품종 다량의 제품 특성으로 제품간 수량과 매출이 반드시 비례하지 않으므로 수량으로 수요 및 성장 등 표현하는데 제한된다. 예로, 낮은 단가의 Low power LED 판매 수가 높은 단가의 High power LED 보다 크더라도 그 합산 매출액은 반대가 될 수 있기 때문이다. 세부적인 내용은 데이터 분석 결과에서 다루기로 하고, 주요 방법론에 대해서 아래와 같다. 그리고, 데이터 분석을 위해 RStudio version 4.0.2을 사용하였다.
Ⅰ. 연도별 매출 자료에 대해 먼저, OLS에 의한 확산 모형으로 모수 m0, p0, q0를 추정하였고, 그 과정에서 이상치를 발견하여 방법의 부적절함을 확인하였다. 이에 이상치 제거 후, 결측치에 통계적 대체법2)(김에덴 외, 2021, Steffen Moritz 외, 2017)을 적용하여 오차항의 자기상관성 고려 추정법을 사용하였다. 이 방법이 적합한 모형임을 확인하였고, 모수를 올바르게 추정하였다. 모형의 적합성은 차경천 외(2009)의 선행연구 방법을 참고하여 비교 평가하였다.
Ⅱ. 수정 추정법에 의한 모수를 초기치로 하여 Bass-NLS 방법으로 mN, pN, qN를 추정한 후, 수정 추정법과 NLS방법으로 추정한 모수들 중, 가장 적합한 모수 선택을 위해 RMSE 등 예측오차 지표들을 측정 비교하였다(Table 2).
Ⅲ. 위 Ⅱ에서 우수한 방법으로 추정된 혁신 및 모방계수(p, q)의 상대적 강도를 통해 제품특징을 분석하였다. Bass 확산모형으로 미래의 당기 및 누적수요를 예측하고 당기매출 최대증가율, 변곡점 등 여러 파생 수치를 산출하였다.
Ⅳ. 수정된 추정법에서 구한 잠재적 시장규모 m을 초기값으로 놓고 비선형 성장곡선 모형들(Table 3)에 적용하여 앞서 구한 Bass-NLS 모형과 함께 가장 적합한 fitting 모델을 구하는 등 비교 분석하였다.
ⅰ) 비선형 성장곡선모델링 과정에서 비선형 최소제곱방법으로 직접 모수 추정 시, NLS처럼 잘못된 초기값 때문에 비수렴성 문제가 발생할 수 있으며, 특히 잠재적 시장 규모(m)은 초기값에 가장 민감한 영향을 주는 것으로 알려져 있다(강현철 외, 2001). 이에, 적합한 초기값을 얻기 위해 모형의 비선형을 선형 form으로 변환하고 수정 추정법에서의 m을 적용하여 선형회귀분석을 통해 나머지 두 개의 모수를 추정하였다.
ⅱ) 위 ⅰ)에서 비선형 성장곡선모형의 선형 form을 회귀분석한 모수에 대해 t-검정, F-검정, 결정계수(R-squared) 등 검정통계량을 확인하고, 초기값을 구하였다.
5. 데이터 분석 모델 및 결과5.1 OLS와 자기상관성을 고려한 추정법의 모형 적합성 비교 결과우선, Bass-OLS 방법으로 추정한 결과, 더빈-왓슨(DW) 통계량에서와 같이 수치적으로 잔차들은 서로 상관성이 없는 독립관계로 나타내었다(Table 5). 그러나, 잔차 그래프 Fig 3(a)를 보면 양의 상관성이 있는 것처럼 보이며, 13번째 데이터가 이상치임을 확인하였다. 이에, 올바른 모형 수립을 위해 이상치를 제거하고, 시계열 데이터이므로 시간 동기화를 맞추기 위해 결측치 시점에 통계적 기법에 의한 적절한 값을 대치하였다. 사용된 데이터는 단일변량을 가지며, 증가하는 추세 구간 내에 있으므로 결측치 대체값은 단순대입법을 적용하였다(김에덴 외, 2021). 결측치 대체 적용 데이터에 대해 OLS 추정 결과, DW=0.947으로 DW 통계량은 0에 가깝고 p-value도 0.0013으로 낮아 잔차들은 양의 상관관계를 갖는 것으로 나타났으며, Fig 3(b)와 같이 잔차 그래프에서도 양의 상관성을 비교적 명확하게 나타내었다.
Fig 4는 이상치를 제거하고 결측치 대체법을 적용한 모형 잔차에 대한 자기상관함수(ACF : Auto Correlation Function) 및 부분자기상관함수(PACF : Partial Auto Correlation Function) 그래프를 나타낸 것이다. Fig 4에서도 잔차 사이에 자기 상관관계가 존재함을 확인할 수 있으며, 이 그래프를 통해 식 (2-9)에서 차수(order) h=1로 두고, 오차항의 자기상관성을 고려한 수정된 모형을 통해 다시 분석하였다.
추정 분석 결과, Table 5와 같이 자기상관성 고려 추정법은 DW=1.624으로 비교적 2에 가깝게 나타내었고, p-value는 0.0496으로 거의 임계치 0.05를 나타내어 잔차들은 자기상관성이 없는 것으로 일단 추정하였다. 이에 보다 명확한 판단을 위해 데이터 크기와 회귀모형의 Regressors에 따른 유의수준 0.05의 DW 통계표(Savin and White, 1977)를 사용하였고, 데이터 크기 n=16, Regressors k=3을 적용한 결과, dL(DW하한치)=0.857, dU(DW상한치)=1.728이므로 이 모형은 잔차의 독립성을 만족함을 확인하였다. 또한, Fig 3(c)와 같이 자기상관성을 고려한 모형의 잔차 그래프를 보면 잔차들은 비교적 무작위적(Randomness)으로 분포되어 나타났고, Fig 5의 ACF, PACF 그래프에서도 잔차 사이에 자기상관성이 없음을 나타냄으로써, 오차항의 자기상관성을 고려한 모형이 적합하고 올바른 추정 방법임을 확인하였다.
그리고, 이 추정법은 잔차의 분산도 값이 가장 낮았고, 대안 모델 중 가장 적합한 모형을 선택하는데 유용한 척도가 되는 AICc(수정된 AIC, Akaike information criterion)도 가장 낮은 값을 나타내며 OLS 보다 적합한 모형임을 추가 확인하였다. 여기서 N은 관측치의 수이고 K는 추정된 모수의 수일 때 AICc는 식 (5-1)과 같이 정의된다.
참고로, 표본 크기 대비 모수가 너무 많으면 성능이 저하되므로 Burnham과 Anderson(2002)은 추정된 모수의 수에 대한 관측치 수 비율이 작을 때(비율 < 40) AICc를 사용할 것을 제안하였다(차경천 외, 2009).
5.2 BASS 모형의 자기상관성 고려 추정법과 NLS 방법의 추정치 비교 결과위에서, 오차항의 자기상관성을 고려한 Bass 확산 모형으로 모수 추정한 결과, 자기상관 오차항의 계수(order=1) =0.5110, m=1162.06, p=0.0055, q=0.3419으로 추정하였다. 여기서, 혁신계수 p보다 모방계수 q가 훨씬 크게 나타났으므로(q > p) 우선 Bass 모형 수식에서 볼 때, 성장곡선모형에 대해서 시간에 따라 증가하다가 일정값(최대값)을 지난 후, 다시 점차 감소하는 로지스틱 모형에 가까울 것으로 추정하였다. 이와 관련한 자세한 분석은 나중에 여러가지 성장곡선모형 분석에서 밝히기로 한다. Bass-NLS 방법은 앞서 추정한 m, p, q를 초기치로 하여, 모수 mN=1338.13, pN=0.0026, qN=0.3003을 추정하였다. 보통 Bass 모형을 적용한 다른 사례연구에서 OLS 방법의 경우, NLS보다 과소추정하는 경향이 있는데, 본 연구에서도 수정 추정법이 NLS보다 다소 과소추정됨을 확인하였다. NLS 방법에 의한 모방계수 qN도 혁신계수 pN보다 훨씬 크기 때문에 성장곡선모형에서 앞에서와 마찬가지로 로지스틱 모형에 가까울 것으로 일단 추정하였다.
이러한 수정 추정법과 NLS 추정법 중, 성능이 가장 우수한 모형을 선택하기 위해 Table 7과 같이 RMSE, MAE, MAPE 등 예측오차를 측정 비교하였다. 측정 분석 결과, NLS 추정방법이 수정 추정법보다 더 작은 예측오차를 주는 것으로 확인되었다(예측오차 평가지표 설명은 위 Table 2 참고). 다만, MPE의 경우 수정 추정법에서 더 작게 나타나는데, 이 지표는 상대적 예측오차를 비교하기 위한 방법으로 예측오차의 단순합계를 내므로 전체적인 오차 크기를 비교하기에 적절치 않음을 확인하였다. 따라서, 향후, 모형 비교 시 MPE 지표는 제외하는 것이 타당하다.
5.3 BASS-NLS 모형에 의한 모수 p, q의 상대적 강도자동차 외장 램프용 LED 매출에 대해 Bass-NLS으로 추정한 모수는 p=0.0026, q=0.3003이며, 혁신계수보다 모방계수가 월등히 높게 나타났다(q/p=115.9). Bass 확산 모형은 최초 구매(수요)자의 성장을 모형화 할 때 사용하며, 혁신효과와 모방효과의 두 가지 요소가 확산에 가장 큰 영향을 주는 것을 전제로 한다. 즉, 제품의 시장 출현 이후 확산과정은 대중매체와 같은 외부영향으로 구매하는 혁신자 집단과 이전 채택자 영향(내부영향)에 의해 구매하는 모방자 집단의 선택과정 또는 이러한 두 과정의 결합으로 구분한다(민의정 외, 2014). 여기서, 위의 추정 모수로 볼 때, 자동차용 LED는 내부영향에 의한 구매선택 과정에 가깝다. LED 등 하위부품들은 소비자에게 직접 공급이 아닌 상위, 차상위 제조사에 공급하는 B2B 비즈니스 품목이다. 예로, LED(광반도체)와 유사 하위부품의 전력반도체인 스위칭 소자 MOSFET의 확산수요 연구(김진 외, 2014)에서도 유사한 경향을 볼 수 있는데, MOSFET에 대한 NLS 추정결과, p=0.0006, q=0.05으로, 혁신계수가 모방계수보다 매우 낮게 나타났다. 상대적 강도는 q/p=83.3으로, 위의 LED의 경우와 비교적 유사하다고 볼 수 있다.
아래 Table 9(박도형 외, 2014)는 업종 및 품목 별 모형 계수를 추정한 이전 연구에서 차용한 표이다. 아래 표에서 알 수 있듯이, 전자제품, 컴퓨터, 영상, 음향 및 통신장비 등 첨단산업의 경우 혁신계수 평균치가 높고 금속광업과 같은 원자재 관련 산업은 상대적으로 혁신계수가 낮게 분석되고 있다(박도형 외, 2014). LED와 같은 반도체 부품은 금속이나 원천소재와 같이 순수 원자재는 아니더라도 최종소비자와 가까운 OEM 완성품 업체 기준에서 볼 때, 원자재에 준하는 하위부품 포지션에 있으므로 원천소재 품목의 혁신계수와 일반제조/가공업의 혁신계수 사이에 위치하는 것으로 분석된다.
아래 Table 10은 LED 공급업체 ⇒ 중간제조업체(램프모듈) ⇒ OEM 업체(완성차)의 Supply chain 구조에서 각 부분의 대표업체들의 혁신계수(p)와 모방계수(q)를 나타낸 것이다. 데이터 수집 시점상 일부 차이가 있으나 최대한 유사 시계열에 맞춰 분석하였고, 여기서 OEM 업체의 혁신계수가 높고, LED 공급업체의 혁신계수는 낮음을 알 수 있다. OEM 업체의 높은 혁신계수는 신차에 대한 소비자들의 기대심리와 페이스리프트(Facelift) 명목으로 거의 매년 디자인 변경 출시되는 등 마케팅 의존 효과가 크기 때문인 것으로 생각된다. 이에 대해, 별도 연구과제로 분석하면 의미 있을 것으로 사료된다.
5.4 BASS-NLS 성장곡선모형에 의한 수요예측 분석다음은 Bass-NLS에 의한 성장곡선모형과 이에 의한 수요예측 분석 결과이다. 아래 Fig 7은 연간 당기 및 누적매출에 대한 미래 수요변동을 예측한 그래프이다. 첫 매출 발생연도인 2006년부터 2021년을 지나 미래 수요예측을 추정하였다.
먼저, 잠재적 시장규모(m)는 1338.13M 달러이고, 당기수요 증가율이 최대가 되는 시점 t1과 이때 당기수요 s(t1)은 식 (2-6)과 식 (2-5)에 의해 다음과 같이 나타낼 수 있다. 즉, 당기매출 증가율이 최대인 시점은 11.29(약 2017년)이고, 이 때 당기수요는 68.15M 달러이다. 또한, 당기수요 곡선에서 t1은 변곡점이며, 이 시점을 기준으로 이후 당기수요 증가율은 서서히 둔화되기 시작하는 것으로 나타났다.
다음으로 당기수요가 최대가 되는 시점 t2와 이때 최대 당기수요 S(t2)는 식 (2-7)과 식 (2-5)에 의해 다음과 같이 나타낼 수 있다. 즉, 당기수요 최대 시점은 15.63(약 2021년)이고, 이 때, 최대 당기수요는 102.23M 달러이다. 또한, t2는 누적수요곡선에서 변곡점이며, 누적수요 증가율이 최대가 되는 시점이기도 하다. 이 시점에서 누적수요는 식 (2-4)에 의해 663.19M 달러로 계산되었다. 이 시점 이후, 누적수요 증가율은 서서히 둔화되고 확산 속도가 느려지는 S자형 곡선으로 수렴된다. 당기수요곡선에서 보면 매출은 감소하여 전년대비 성장률은 마이너스를 취하게 된다. Rogers 혁신확산이론 중 혁신채택 5개 집단 구분에 따르면 Late Majority, Laggards 영역으로 진입하게 되는 것이다. 이와 같은 당기수요곡선 및 누적수요곡선 모형은 Vijay Mahajan 외(1990) 연구에서 나타낸 Bass Model 해석구조에 부합하는 것으로 확인하였다.
5.5 여러 가지 비선형 성장곡선모형과 비교한 수요예측 분석지금까지 Bass-NLS 방법에 의한 성장곡선모형을 통해 수요예측 등을 확인하였다. 그러나, Bass 모형 방법뿐만 아니라, 다양한 분야에서 여러 가지 비선형 성장곡선모형들이 개발되어 적용되고 있다. 각 분야의 데이터들은 그들 확산형태에 따라 최적화된 모형을 도입하여 사용하고 있다. 여기서 여러 비선형성장곡선 모형 중, 대표적으로 자주 사용되는 변형지수 모형(Fourt & Woodstock, 1960), 로지스틱 모형(Mansfield, 1968) 그리고, 곰페르츠 모형(Martino, 1976)에 본 데이터를 적용하여 앞서 구한 Bass-NLS 모형과 함께 비교 분석하였다(본문 3절 성장곡선모형 및 Table 3 참고).
비선형 성장곡선모형 수립에 필요한 모수의 초기치를 구하기 위해, 먼저 각 모형의 비선형을 선형 form으로 변환하고, 위에서의 오차항의 자기상관성을 고려한 추정법의 m을 적용하여 선형회귀분석을 통해 모수 a, b를 추정하였다(Table 11).
이와 같이, 추정한 모수를 초기치로 하여 각 비선형 성장곡선모형을 도출하였다. 아래 Table 12는 각 모형들에 대한 최적 모수들이고, Fig 8은 Bass-NLS 모형과 함께 3개의 모형들에 대한 수요예측 그래프이다. 우선, 모수 초기치에 의한 fitting시 로지스틱, 곰페르츠 모형은 이상없이 최적해에 수렴하여 모수가 바르게 추정되었다. 그러나, 변형지수 모형에서는 데이터 추세상 직관적으로도 잠재적 시장규모가 Saturation되는 형태가 아님을 예상했듯이, 비수렴성 문제로 최적 모수 추정에 실패하였다. 앞서, Bass 확산모형으로 분석한 자동차 외장램프용 LED 매출데이터는 혁신자(p), 모방자(q) 모두를 성장요인으로 갖고 있고, 더구나 모방자(q) 효과가 더 우세한 특성을 보면, 혁신자(p) 요인만을 고려한 변형지수 모형에는 적합하지 않다고 할 수 있다. 즉, 기술적 분석, 모형 요인적 분석 모두에서 적합하지 않은 것이다. 다른 성장곡선 모형들과 그래프 비교를 위해 모수 초기치를 임의 조정하여 fitting하였고, 잠재적 시장규모(m)가 그래프상 무한대로 나타나 성장곡선모형으로 적합하지 않고, 뒤의 비선형 모형 선호 통계량 계산 결과에서도 변형지수 모형은 부적합한 것으로 확인하였다.
반면, Bass-NLS, 로지스틱, 곰페르츠 모형에서는 잠재적 시장 규모 m값에서 각 모형별 차이가 있으나, 대체로 모두 적합한 fitting과 모수 추정을 나타내었다. 이것은 변형지수 모형 외 3개 모형은 모두 모방자(q) 요인 효과를 가지고 있으며, 특히, 모방자(q) 요인만을 고려한 로지스틱 모형을 감안하면 자동차 외장램프용 LED 시장성장은 모방자(q) 요인효과가 매우 높은 것으로 분석될 수 있다. 실제 현업에서 고객들은 LED 선택 시, 제품가격 요건도 중시하지만 대체로 주요 LED 공급사를 별도 관리하면서 이전 양산프로젝트에 LED가 채택된 경험을 바탕으로 심각한 품질문제가 제기되지 않는 한, LED 공급사 또는 해당제품을 다시 채택하려는 경향이 높은 것과 유사한 측면이 있다.
다음은 추정한 비선형 성장곡선모형들에 대해 모형선호 기준 통계량을 비교한 결과이다(Table 13). 모든 지표에서 곰페르츠 모형이 가장 적합한 성장곡선모형으로 나타났다. 특히, UI와 U값이 0에 가깝게 보였고, MAPE값에서도 0과 10% 사이로 나타나 모형 예측은 매우 정확한 것으로 판정하였다.
잠재적 시장규모(m) 비교 시, 곰페르츠 모형에서 m=$2864.018M으로 상대적으로 크게 추정되었고, Bass-NLS 모형은 m=$1338.13M, 로지스틱 모형은 m=$1109.094M으로 과소추정 되었다. 이처럼, 추정된 m에 대해 완성차 또는 램프제조사 등 현 업계의 생산계획, 수요 등 직접적 자료가 있으면 보다 정확한 분석이 가능하겠으나, 곰페르츠 모형이 시장 초기 빠른 성장을 보이는 제품 확산 예측에 적합하다는 특징(박도형 외, 2014)을 고려하면, 이 모형의 m이 과다추정이라고 단정하기는 어렵다. 2000년대 초부터 RCL, CHMSL 등 후방램프를 시작으로 LED는 2009년 국내최초 에쿠스 리무진 LED 헤드램프에 적용(세계최초는 2007년 렉서스 LS500h) 이후, 약 20여종의 자동차 램프 적용 채택에서 비약적으로 증가하였다(이동원 외, 2013). 아울러, EU/북미를 시작으로 국내에서 자동차 램프는 친환경, 안전, 에너지효율 등을 이유로 의무장착 법규가 시행되어 LED 급성장에 영향을 끼친 것도 이 무렵이다. 더구나, 전기차, 자율주행차 등 자동차의 패러다임이 변하고 있는 요즘을 보면 높게 추정된 잠재적 시장규모를 더욱 긍정적으로 전망할 여지가 있다. 이에, 현재 대체광원이 없는 한 자동차 램프용 LED의 잠재적 시장규모는 $1338.13M에서 $2864.018M으로 추정해 볼 수 있다. 참고로, 변형지수 모형에 대한 모형선호 기준 통계량 측정 결과, MAPE 값에서 30%를 벗어나 모형이 적합하지 않음을 위와 마찬가지로 확인하였다.
6. 결 론본 연구에서는 Bass 확산 모형에 의한 혁신계수(p) 및 모방계수(q)를 구하고 국내 자동차 외장 램프용 LED의 확산형태와 상대적 강도를 통해 제품특성에 대해 알아보았다. 또한, 성장곡선모형을 구하여 시장 수요예측 및 당기, 누적매출 변곡점 등 여러 파생 수치도 분석하였다. 다양한 비선형 성장곡선모형을 추가 도입하여 Bass-NLS 성장곡선 모형과 비교 분석하였고, 보다 최적화된 모형을 도출하였다. 이에 대해 다음과 같이, 결론을 정리하였다.
첫째, Bass-OLS 방법은 오차의 자기상관성으로 인해 모형에 적합하지 않으므로 이를 고려한 수정된 추정법을 도입하였다. 차수(Order) 1의 자기상관성을 고려한 추정법이 데이터에 적합한 모형임을 확인하였다. 이러한 수정 추정법과 NLS 방법으로 각각 모수 m, p, q를 추정하였고, RMSE 등 예측오차들을 측정하여 정확도를 서로 비교하였다. 그 결과, NLS 방법의 오차가 더 낮으므로 NLS 방법이 상대적으로 정확한 모형이라고 할 수 있다.
둘째, NLS 방법으로 혁신계수 p=0.0026, q=0.3003으로 추정하였고, 혁신계수보다 모방계수가 크게 나타났다. LED는 광반도체로 전자산업에서 핵심 하위부품이며, 동등 하위부품 반도체인 MOSFET의 상대적 강도에서도 이와 유사한 경향을 나타냈다. LED 등 하위부품들은 소비재나 상용 산업재처럼 광고, 마케팅과 같은 외부효과보다는 램프제조사 또는 완성차 업체 등으로부터 이전 프로젝트에 적용된 경험, 제품의 신뢰성, 품질인증 및 평가 등을 거쳐 채택되는 내부영향 때문인 것으로 분석된다. 위의 Table 9와 Table 10과 같이, 이들 혁신계수는 원천소재 품목과 일반제조/가공업의 p값들 중간에 위치하거나 Supply chain 구조에서 낮은 p값을 나타내었다.
셋째, Bass-NLS 확산모형에 의한 성장곡선모형 분석 결과, 잠재적 시장규모(m)는 1338.13M 달러로 나타났다. 그리고, 당기수요 증가율 최대 시점 t1은 11.29(약 2017년)이고, 이 때 당기수요는 68.15M 달러로 나타났다. 시점 t1은 당기수요 곡선에서 변곡점이 되며, 이 시점 이후, 당기수요 증가율은 점차 둔화되는 것으로 확인되었다. 당기수요 최대 시점 t2는 15.63(약 2021년)이고, 이 때 최대 당기수요는 102.23M 달러로 나타났다. 시점 t2는 누적수요곡선에서 변곡점이며, 누적수요 증가율 최대 시점이기도 하다. 이 때, 누적수요는 663.19M 달러로 계산되었다. 이 시점 이후, 누적수요 증가율은 서서히 둔화되고 확산속도가 느려지는 S자 곡선으로 수렴된다.
넷째, 가장 적합한 비선형 성장곡선모형 도출을 위해 대표적인 모형인 ‘변형지수’, ‘로지스틱’, 그리고 ‘곰페르츠’ 모형을 제안, 모델링하였고 Bass-NLS 모형과 비교 분석하였다. 이들 비선형 모형에 대한 최적 모수 추정을 위해 모형의 비선형을 선형으로 변환한 후, 회귀분석을 통해 모수의 초기치를 추정하였다. 이러한 초기치를 가지고 모형 적용 분석 결과, 모방자(q) 효과를 가진 로지스틱, 곰페르츠 그리고 Bass-NLS 모형에서 적합한 fitting과 최적 모수를 추정하였다. 이들 중, 모형선호 기준 통계량에서 곰페르츠 모형이 가장 우수한 모형임을 확인하였다. 잠재적 시장규모 m은 곰페르츠 모형에서 가장 높았고, Bass-NLS, 로지스틱 모형 순으로 나타났다. 자동차 외장램프 LED 시장 초기 매출 급성장이 시장 초기에 빠른 성장의 제품 확산 예측에 적합한 곰페르츠 모형 특징에 부합함을 보면 m=$2864.018M은 과다추정으로 보기 어렵다. 변형지수 모형은 모수 추정의 비수렴성을 보였고, 혁신자(p) 효과만을 고려한 성장곡선 모형으로 자동차 외장램프 LED 시장성장 특징에도 적합하지 않은 것으로 분석되었다. 또한, 통계량 MAPE도 30%를 벗어나 모형에 적합하지 않음을 확인하였다.
자동차 램프산업에 LED가 처음 적용된 이후, 근래의 자동차 기술 및 모델수준에서 자동차용 LED 매출에 대해 Bass-NLS 확산모형을 적용하여 미래 수요예측 및 여러 특성 등을 분석하였다. NLS 모형이 일반적으로 OLS 또는 MLE 방법보다 더 우수하게 평가되나, 모수 p와 m을 과소추정하며, 특히 잠재적 시장규모(m)는 최근 관측치에 수렴하는 경향이 있는데(박도형 외, 2014), 이번 연구에서도 유사한 경향이 확인되었다. 그러나 현재, 자동차 램프에 LED 보급은 전보다 높아졌지만, 여전히 할로겐 램프 등은 사용되고 있고, 차량의 모든 Segment 및 옵션에 LED가 채택된 것도 아니므로 미발생 수요는 남아있다. 또한, 현재의 자동차 기대수요뿐만 아니라, 미래기술의 자기 대체품에 준하는 전기차, 수소차 및 자율주행차 등 시장성장과 여기에 적용될 ADB(Adaptive Driving Beam), AADB(Advanced ADB), Micro-LED Pixel Array, DMD(Digital Micro-mirror Device) 헤드램프 등 자동차 램프의 혁신적 기술이 개발/양산 확대를 앞두고 있어, 자동차 조명장치의 LED 수요는 다시 비약적인 증가를 앞두고 있다(LED inside, 2021). 특히, 미국 리서치 조사업체 Navigant Research 보고서에 따르면 자율주행차 시장규모는 2035년 기준 743조원으로 성장하고, 세계 3대 시장(유럽, 미주, 아시아)에서 자율주행차 보급규모는 9,540만대로 연평균 85%의 놀라운 속도로 크게 성장할 것으로 전망하고 있다(이병윤, 2016).
최근의 Bass 모형의 확장을 위한 후속연구들이 다양한 분야에서 서로의 연구목적을 가지고 이루어지고 있다. 이번 연구와 관련하여, 모수를 추가한 Bass 모형 확장과 모형의 모수 추정방법에 관한 추가적인 연구가 필요할 것으로 보인다. 예로, 시간의 흐름에 따른 모수 p, q, m의 변화에 대해 Augmented Kalman Filter(AKF)를 사용한 모수 변화 추정 방식(Xie et al, 1997)이 기존 NLS 방법보다 더 정확한 예측력을 보이고 있다고 한다. 보다 충분한 데이터 수집과 이러한 Bass 모형의 확장 연구를 적용하여 수요예측의 정확성을 향상시키는 등 향후 과제를 진행하고자 한다.
NOTES1) 현대모비스 홍보동영상 이미지 캡쳐, Head Lamp Technology Roadmap(https://www.youtube.com/watch?v=KyfQnGXeQ10) 2) 여기서 사용된 데이터는 단일변량을 가지고, 증가 추세 구간에 있으므로 결측치 대체값으로 단순대입법을 적용하였고, R에서 ImputeTS 패키지 중, ‘na_interpolation(x)’ 함수를 사용하였다. 3) 이상치 제거로 인한 결측치 대체값. 본 데이터는 단일변량을 가지며, 증가하는 추세 구간 내에 있으므로 통계적 기법 중 단순대입법을 적용하였다. (Fig 6에서 * 표시가 결측치 대체값) 4) Electronic Disclosure System of Financial Supervisory Service. “business Report” https://dart.fss.or.kr/. REFERENCESCha, Kyoungcheon, and Kim, Sanghoon 2009. A Modified Diffusion Model Considering Autocorrelated Disturbances: Applications on CT Scanners and FPD TVs. Asia Marketing Journal 11(1):29-38.
Electronic Disclosure System of Financial Supervisory Service business Report https://dart.fss.or.kr/..
Fourt, LW, and Woodlock, JW 1960. Early Prediction of Market Success for Grocery Products. Journal of Marketing 25(2):31-38.
Global Economic 2021. Korea Motors re-enters the top5 producers ... Electrical vehicles, luxury cars, and SUVs are leading the way. https://cmobile.g-enews.com/view.php?ud=20210208111805270183a046ffa0_1&ssk=newmain_0_2&md=20210208135651_R..
Ha, Youngwook, Jo, Sunmoo, and Park, Myoungchul 1999. Forecasting the Number of AO/DI Subscribers. Journal of Korea Technology Innovation Society 1999(11):29-43.
Journal, HMG 2018. High beam, Don’t think about whether to turn it on or not. https://news.hmgjournal.com/Tech/mobis-aadb-headlamp-tech..
Hong, Jungsik, and Koo, Hoonyoung 2012. Comparison of the Bass Model and the Logistic Model from the Point of the Diffusion Theory. Journal of the Korean Operations Research and Management Science Society 37(2):113-125.
Hong, Jungsik, Kim, Taegu, and Koo, Hoonyoung 2011. A Parameter Estimation of Bass Diffusion Model by the Hybrid of NLS and OLS. Journal of the Korean Institute of Industrial Engineers 37(1):74-82.
Hwang, Jungyeon 1997. A Study on the Analysis Procedures of Nonlinear Growth Curve Models. Journal of the Korean Society for Quality Management 25(1):44-55.
Kang, Hyuncheol, and Choi, Jong Hoo 2001. A Study on the Demand Forecasting using Diffusion Models and Growth Curve Models. The Korean Journal of Applied Statistics 14(2):233-243.
Kim, Eden, Go, Seokgap, Son, Seungchul, and Lee, Byeongtak 2021. Technical Trends of Time-Series Data Imputation. ETRI Electronics and Telecommunications Trends 36(4):145-153.
Kim, Gene, and Khoe, Kyoungil 2014. Estimation of Semiconductor Market, Using NLS Diffusion Model. Journal of Digital Convergence 12(3):141-147.
LED inside 2021. TrendForce 2020–2021 Global Automotive LED Product Trend and Regional Market Analysis. https://www.ledinside.com/node/32076..
Lee, Byoungyoon 2016. Trends and Prospects for Technology Development for Self-driving Vehicles at Home and abroad. Information & communication 33(4):10-16.
Lee, Dongwon, and Lee, Sanggi 2013. Technology Market Analysis for Developing LED Headlamp for Vehicles. Korea Institute of Science and Technology Information.
Lee, Gunhee, and Lee, Chung-kun 2002. A Comparison Study of Demand Forecasting Techniques using Growth Curve Models. Sogang Journal of Business 13(2):195-228.
Lee, Seunghoon, Yoon, Yeonah, Jung, Jinhyeong, Sim, Hyunsu, Chang, Taiwoo, and Kim, Youngsoo 2020. A Machine Learning Model for Predicting Silica Concentrations through Time Series Analysis of Mining Data. Journal of Korean Society for Quality Management 48(3):511-520.
Lee, Yegyoung, Lee, Hyunjeong, Jang, Hyeonae, and Shin, Sangmun 2021. Development of a New Similarity Index to Compare Time-series Profile Data for Animal and Human Experiments. Journal of Korean Society for Quality Management 49(2):145-159.
Liu, Yiqi, and Jung, Uk 2021. Density Adaptive Grid-based k-Nearest Neighbor Regression Model for Large Dataset. Journal of Korean Society for Quality Management 49(2):201-211.
Mahajan, V, Muller, E, and Bass, FM 1990. New product diffusion models in marketing: A Review and Directions for Research. Journal of Marketing 54: 1-26.
Martino, JP 1976. Technological Forecasting for Decision Making. New York. American Elsevier.
Min, Yuijoung, and Lim, Kwangsun 2014. Comparative Evaluation of Diffusion Models using Global Wireline Subscribers. Journal of Information Technology Applications & Management 21(4):403-414.
Park, Dohyoung, Jung, yeojin, Jung, jaekwon, and Lee, dongwon 2014. The Research on Growth Curve for Advanced Market Estimation. Korea Institute of Science and Technology Information.
Park, Jongwon 2012. Automotive application status of LED and the trend of developing a package for Headlamp. Journal of the Korean Institute of Electrical and Electronic Material Engineers 25(8):5-11.
Rogers, EM 1962. Diffusion of innovations. New York. The Free Press.
Savin, NE, and White, Kenneth J. 1977. The Durbin-Watson Test for Serial Correlation with Extreme Sample Size or Many Regressors. Econometrica 45(8):1989-1996.
Srinivasan, V, and Mason, CH 1986. Nonlinear Least Squares Estimation of New Product Diffusion Models. Marketing Science 5(2):169-178.
Moritz, Steffen, and Bartz-Beielstein, Thomas 2017. ImputTS: Time Series Missing Value Imputation in R. The R Journal 9(1):207-218.
Xie, Jinhong, Song, M., Sirbu, M., and Wang, Q. 1997. Kalman Filter Estimation of New Product Diffusion Models. Journal of Marketing Research 34(3):378-393.
Yang, Jinah, Min, Daiki, and Choi, Hyungsuk 2017. Long-Term Projection of Demand for Reverse Mortage Using the Bass Diffusion Model in Korea. Journal of the Korean Operations Research and Management Science Society 42(1):29-41.
Yim, Eunyoung, and Jang, Gyoungpil 2018. Sector Update, Automotive. Samsung Securities Co., Ltd. pp 1-35.
Figure 2.A model according to the relation between the innovation coefficient (p) and the imitation coefficient (q) 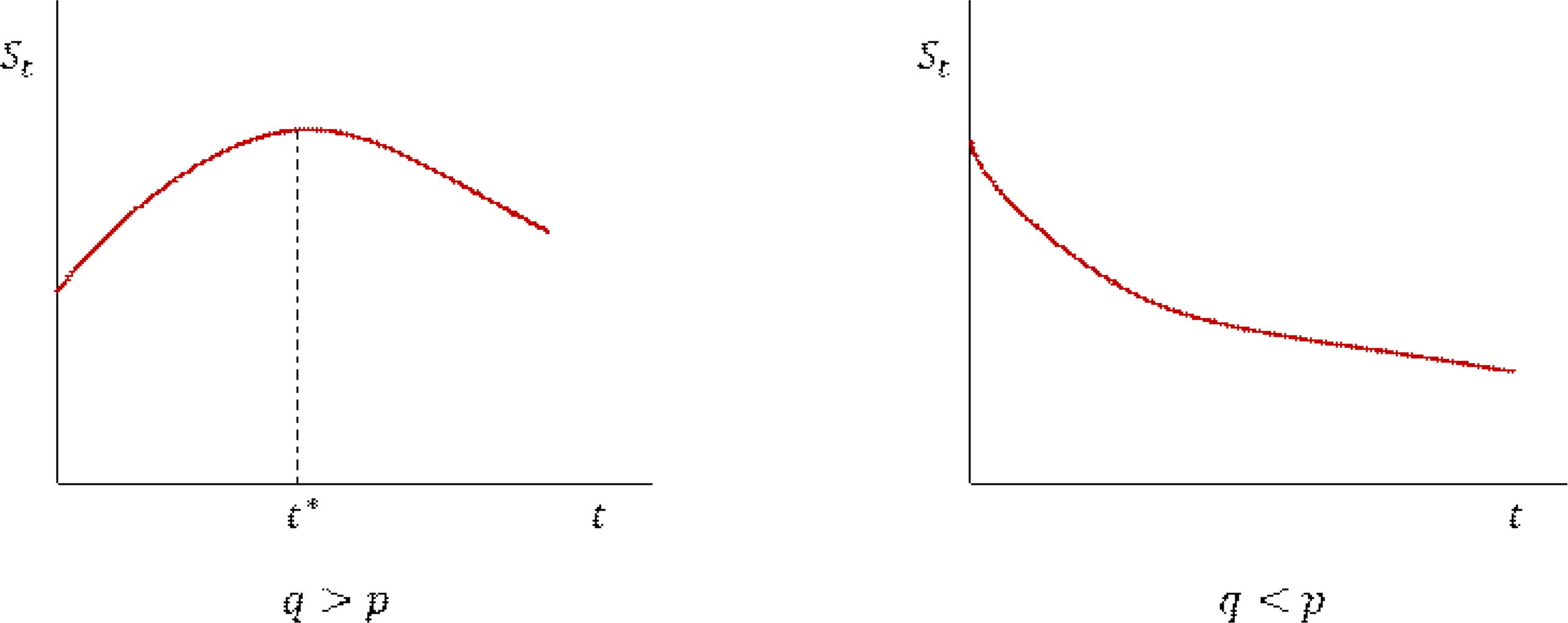
Figure 3.Residuals graph, (a) OLS, (b) Remove outliers and replace missing values, (c) Autocorrelation model 
Table 1.Comparison of various growth curve models
Table 2.Various prediction error evaluation indicators for the models Table 3.Nonlinear and linear form of various nonlinear growth curve models Table 4.Model preference criterion statistics for nonlinear growth curve models (Hwang, jungyeon, 1997)
Table 5.The estimation results for each models Table 6.Comparison of each parameter m, p, and q estimated by Autocorrelation model and NLS methods Table 7.Estimation results of several prediction error indicators for Autocorrelation model and NLS methods
Table 8.Annual sales by year predicted by Autocorrelation model and NLS methods compared to actual data Table 9.The Mean and SD of coefficient estimates of Bass models by major classification Table 10.p and q for each company in the LED Lamp supply chain structure of automotive Table 11.The results of the parameter and model suitability test for linear form Table 12.Parameter estimation results for nonlinear growth curve models Table 13.Comparison of measurement of model preference statistics for nonlinear growth curve models |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||