1.서 론
2019년 12월 중국 후베이성 우한시에서 발견된 새로운 코로나바이러스(SARS-CoV-2)는 사람 간의 전파를 통해 전 세계적으로 폭발적인 발생을 일으켰다(Mizumoto et al., 2020). 당시에는 폐렴 증상과 같다고 해서 우한 폐렴(Wuhan pneumonia)으로 불리었으나, 2020 년 1월 7일 원인 병원균은 새로운 코로나 바이러스로 확인되었으며 이 바이러스는 SARS 바이러스 및 MERS 바이러스와는 다르지만 밀접하게 관련되어 있다고 밝혀졌다 (Park, 2020). 이후 세계보건기구(WHO)에서는 임시로 Novel coronavirus라는 표현을 사용하였다(대한민국 정부에서는 해당 명칭을 직역한 ‘신종 코로나바이러스감염증’의 표현 사용) (Park, 2020). 이후 2020년 2월 11일에 WHO에서 이 감염증의 공식 명칭을 COVID-19로 확정함에 따라 대한민국 정부에서는 해당 명칭을 ‘코로나바이러스감염증-19’의 표현을 사용하였다(WHO, 2020). 초기에는 SARS 및 MERS보다 덜 심각 할 수 있다고 알려졌으나, 급속도로 증가하는 사람들 사이에서 발생하는 질병 및 인간 대 인간 전염의 증거가 증가함에 따라 SARS 및 MERS보다 감염성이 큰 것으로 추정되었다(Park, 2020). 실제로, 폭발적인 증가추세에 따라 세계보건기구(WHO)에서는 지난 3월 팬데믹 선언을 하였는데(WHO, 2020), 이는 1968년 홍콩 독감, 2009년의 신종플루에 이어 세 번째이며(김영만, 2020), WHO 이전의 페스트, 콜레라에 준하는 또는 그 이상의 위험성을 의미한다고 말할 수 있다.
질병의 진원지인 중국 후베이성 지역에서는 2019년 12월 발생 기하급수적인 추세로 감염자가 증가하였다. 2020년 7월 31일 현재 중국에서는 4,634명의 사망자를 포함한 84,292명의 확진자를 기록하였다. 다행히도 2020년 2월 15일 이후로 일일 확진자가 감소하기 시작하여, 3월 13일 첫 한자리 수를 기록한 뒤 현재까지도 유지 중이다. 중국에서는 감염력이 감소하여 사실상의 종식상황이 이루어진 반면, 대한민국, 이탈리아, 이란, 독일 및 프랑스를 포함한 중국 이외의 100개국 이상에서 66만명 이상의 사망자를 포함한 1,714만명의 확진자를 발생시켰다(WHO, 2020). 특히 대한민국은 중국 다음으로 코로나-19가 대유행한 나라였고, 3월 중순까지 꾸준히 증가하다가 비교적 짧은 기간 내에 급격한 감소 추세를 보여 4월 중순 이후로 일일 확진자수 한자리 대를 기록하기도 하였다. 그러나 5월부터 7월까지 일일 확진자가 30~100명대를 기록하며 소규모 감염이 계속 이루어지고 있다(MOHW, 2020). 따라서 이러한 대한민국의 사례를 꾸준히 모니터링, 실시간 분석하여 감염력을 판단하고, 다양한 공중 보건적 조치의 영향을 평가하는 것은 전 세계적인 코로나-19 방제와 예방을 위해 공중보건학적 관점에서 매우 중요하다.
대한민국의 첫 번째 코로나-19 사례는 2020년 1월 20일에 확인되었으며, 첫 번째 사례와 두 번째 사례는 모두 해외 입국자이며 공항에서 탐지되었으나, 세 번째 사례부터는 지역 감염을 야기했다(MOHW, 2020). 그러나 2020년 2월 18일까지는 하루 평균 1~2명의 환자가 발생하였으며 우한과 같은 지수증가의 형태가 보이지 않았다. 그러나 2020년 2월 19일 이후로 급격히 증가하기 시작했으며, 2020년 2월 29일 일일 확진자수 909명을 기록하기도 하였다(MOHW, 2020). 이는 2020년 2월 9일과 2020년 2월 16일에 대구광역시 남구에 소재한 신천지증거장막성전(신천지)에서 있었던 예배로부터 기인한 것으로 밝혀졌으며, 대략 대한민국에서 절반 가량의 확진자가 이와 관련 있다고 알려졌다. 이 외에도 경상북도 청도 대남 병원, 충청남도 천안 체육관, 이스라엘 성지 순례 등 다양한 군집 단위 전파가 이루어졌다(Shim et al., 2020).
코로나-19에 대응하기 위해 대한민국 정부는 2020년 2월 23일 코로나-19 경보 수준을 최고수준 ‘심각’으로(Level 4) 격상시켜 감염 통제 강화를 포함한 포괄적인 사회적 조치 이행을 촉진시켰다(MOHW, 2020). 대표적인 예로 대중교통 제한, 모임 제한, 생활 방역, 학교 폐쇄, 고강도 사회적 거리두기 캠페인 등을 시행했으며, 이에 대한 효과로 4월 19일 첫 일일 확진자 한자리 수를 기록하였고, 이는 5월 중순까지 유지되었다(MOHW, 2020). 그러나, 5월 6일 이후 약화된 사회적 거리두기 캠페인을 시행한 이후, 2020년 5월 31일 현재까지도 이태원 클럽, 쿠팡 물류센터, 인천 개척교회 등의 소군집 단위 전파가 지속되고 있다(MOHW, 2020). 더욱이 초, 중, 고등학교가 순차적으로 개학하면서 학교 내 감염 전파에 대한 위험성도 대두되고 있다. 따라서, 지금까지의 사례 분석을 통해 앞으로의 전파속도 또는 전염력을 예측하여 이에 맞는 보건 전략 제시가 필요하다. 이를 위해서는 실시간으로 얻어지는 데이터를 통해 감염력을 분석하고 예측하는 연구는 매우 중요하다고 할 수 있다.
2019년 12월 중국에서 첫 사례가 발견된 후 Lauer, Du, Nishiura 등에 의해 코로나-19의 감염역학적 특성에 대한 연구가 활발히 이루어 졌다(Jung et al., 2020; Lauer et al., 2020; Nishiura et al., 2020; Nishiura and Kobayashi, 2020). 이들은 잠복기의 분포가 중앙값 5.1일이고 97.5%의 환자들이 11.5일 이내에 증세가 나타난다고 조사하였으며(Lauer et al., 2020), serial interval의 분포가 중앙값 4.0일인 로그정규분포의 형태를 보임을 연구함으로써(Nishiura et al., 2020; Nishiura and Kobayashi, 2020) 감염력 측정에 대한 여러 가지 도구들을 제공하였다.
대한민국의 사례에서 감염력 측정을 위한 연구가 다수 진행되었는데, 대한민국의 사례에서는 Shim et al.(2020(2))이 선행된 연구이다. 이 연구는 대한민국의 2월 26일까지의 감염 데이터로 성별, 연령별, 클러스터별 분석을 통해 남성, 80대 이상의 감염력이 유의미한 수준으로 높다는 것을 밝혔고, 4개의 클러스터별 감염력을 측정하였다. 또한, 1월 12일부터 2월 26일까지 대한민국의 데이터와 일반화된 선형 출생 모델(Generalized growth mod-el)로부터 추정된 실질감염재생산수가 1.5(1.4~1.6, 95% 신뢰수준)임을 보였다. Jeong et al.(2020)은 3월 13일까지 7,755명의 확진 데이터를 이용하여 잠복기 및 확진 이후 퇴원까지의 기간 등을 조사하였다. 이 자료를 바탕으로 Kim et al.(2020)은 1월 20일부터 3월 15일까지의 데이터를 바탕으로 SEIR(susceptible-exposed-in-fected-recovered) 모델을 이용하여 실질감염재생산수를 추정하였다. 이 연구를 통해 31번 확진자로부터 신천지에서 일어난 감염 때문에 평균 감염력이 20배 증가하였으며, 2월 28 이후로 실질감염재생산수가 1 이하로 감소할 정도로 국가와 국민의 적극적인 예방 대책이 이루어 졌다는 사실을 보였다. 또한 Shim et al.(2020(1))은 5월 9일까지의 사망 데이터를 이용하여 사망 위험(case fatality risk, CFR)을 추정하였다. 이를 통해 경북지역과 대구지역의 CFR 추정치는 각각 25.9%(19.6~33.6%, 95% 신뢰수준), 20.8% (18.1~24.0%, 95% 신뢰수준)이고 이는 다른 지역의 1.7%에 비하여 월등히 높다는 사실을 보임으로써, 대구와 경북지역의 감염력이 상당히 높았음을 보였다. 또한 Jo et al.(2020)은 딥러닝 기술의 일종인 심층 신경망(Deep neural network)을 이용하여 2월 7일부터 3월 30일까지 코로나-19의 시간에 다른 감염력(transmission rate)과 감염지속기간(infected period)을 SIR(susceptible-in-fected-recovered) 모델을 이용하여 측정하였다.
위의 결과들은 질병 전파의 초기의 데이터를 이용하여 시행된 결과이며, 본 연구는 기존의 출판된 논문들에 이어 2020년 7월 31일까지 보고된 대한민국 내 코로나-19 사례를 바탕으로 수리적, 통계적 방법으로 분석하여 감염력을 판단하고, 공중보건적 조치를 평가하는 것이다. 이에 따라 대한민국에서 코로나-19 발병 사례를 변수화 한 결정론적 수학 모델(Growth model)과 확률론적 수학 모델(Yule-Furry model)을 산술평균하여 사용, 2020년 7월 31일까지 보고된 현지 사례의 확진, 사망 데이터를 이용하여 대한민국에서 코로나-19의 감염 가능성과 심각성을 조사하였다. 기초감염재생산수를 통해 대한민국에서 코로나-19의 감염력을 수치화 하였으며, 세대기간별로 실질감염재생산수를 추정함으로써 시간에 따른 국가적인 공중보건적 조치의 영향을 평가하였다.
2.감염재생산수의 정의 및 추정 방법
2.1 감염재생산수의 정의 및 특징
2.1.1 기초감염재생산수(Basic reproduction number)의 정의와 특징
기초감염재생산수(Basic reproduction number, R0) 는 감염자가 없는 인구집단에 처음으로 감염자가 발생하였을 때 첫 감염자가 평균적으로 감염시킬 수 있는 2차 감염자의 수를 나타낸 것이다(Jones, 2007). 이 지수는 감염병이 각 감염 세대별로 전파되는 수를 수치로 나타내는 지수이다. 이 지수의 개념은 George Macdonald가 말라리아와 같은 모기매개 병원균 전파에 관한 수학적 모델개발 연구를 통해 정립하였다(Macdonald, 1952).
R0가 1보다 크다면, 최소 한 사람 이상이 추가적으로 감염될 수 있다는 뜻이며, 이 경우 감염병이 인구 집단 내에서 대확산 될 가능성이 발생한다(Jones, 2007). R0는 각 감염병마다 주어진 고유한 수치가 아니다. 똑같은 감염병에 감염되더라도 감염자가 속해 있는 집단의 인구 밀도, 사람들 간의 접촉 패턴의 차이 등에 따라 수치가 달라질 수 있다 (Kahn, 2020). 이처럼 동일한 감염병이라고 해서 R0가 항상 같은 것은 아니지만 그럼에도 불구하고 다른 집단 내에서 발병한 동일한 감염병에 대해서는 대체로 유사한 범주 내의 수치를 보이는 편이다(Kahn, 2020).
이 지수는 초기 감염병 연구에서 중요한 지수이다. 실제로, 2015년 대한민국에서 발생한 메르스(MERS-CoV) 집단 감염 사태는 R0의 공중보건학적 중요성을 보여준다. 당시 대한민국 내 메르스 감염의 초기 대응에는 여러 문제점이 지적되었는데 그 중 하나로 언급되는 것이 R0에 대한 잘못된 보건정책적 판단이다. 당시 대한민국 최초 메르스 환자가 발생했을 때 보건복지부는 기존 R0가 0.6~0.8 수준이라는 자료에 근거하여 우리나라에서 감염력이 높지 않을 것이라고 발표하였으며, 이로 인하여 슈퍼관리자에 대한 관리 필요성을 간과한 것으로 평가 받기도 한다.
2.1.2 실질감염재생산수의 정의와 특징
질병의 발생 초기에는 기하급수적 증가 패턴을 보이나, 질병이 진행될수록 백신이나 면역, 방제 전략 등으로 인해 초반과 같은 증가 패턴을 보이지 않는다. 따라서 기초감염재생산수를 사용할 수 없다. 실질감염재생산수(Effective reproduction number, Rt)는 일정부분 면역이 있는 집단이나 방제가 이루어지는 상황에서 각 시간별로 감염자가 발생하였을 때, 그 감염자로 인해 평균적으로 감염되는 감염자의 수를 나타낸다(Jones, 2007). 따라서, 한 명의 환자가 평균적으로 감염시키는 환자수에 해당하며, 확산 여부를 판단하는데 실용적인 지표가 될 수 있다.
2.2 감염재생산수의 추정
본 연구에서는 결정론적, 확률론적 선형 출생 모델(stochastic linear birth process)을 이용하여 기초감염재생산수를 추정하여 비교 및 앙상블 한다. 또한, 각 시간에서 이전 세대 감염자에 의해 생성된 평균 감염자 수인 실질감염재생산수(effective reproductive number,Rt)를 결정론적 선형 모델을 이용하여 추정한다. 아래에 제시되는 방법은 Wallinga and Lipsitch(2020)에서 제시된 방법이며, 구체적인 추정 방법은 아래와 같다.
2.2.1 Lotka-Euler 방정식
개체수 모델의 일종인 Lotka-Euler 방정식을 소개한다. Lotka-Euler 방정식은 연령 분포가 있는 개체군의 성장을 표현하는 모델이다. 이 모델은 Leonnard Euler가 특수한 형태에 대한 방정식을 세웠으며, 이를 바탕으로 1911년 Afread J. Lotka가 일반화 한 모델이다 (Wallinga and Lipsitch, 2020). 먼저 Lotka-Euler 방정식의 가정은 아래와 같다.
(H1) 이 모형은 개체군의 암컷만을 다룬다.
(H2) 모든 개체는 연령 a까지 살아있다면, 일정한 출산율 n(a)를 가진다. (단, n(a)는 연령 a까지 생존하는 개체의 비율과 연령 a인 암컷에 의한 출산율의 곱으로 정의한다.)
b(t)를 시각 t에서의 출생 수라고 정의하자. 그러면 연령 a인 사람들(b(t-a))이 살아남아서 각자 출산율 n(a)로 출생하는데, 이것을 모든 연령(0 ≤ a ≤ ∞)에 대해 모두 합하면 현재 시각 t에서의 총 출생수를 계산할 수 있다.
다음으로, 인구 증가를 기하급수적 증가(지수적 증가, exponential growth)로 가정하자. 이 가정은 Malthus의 인구 모델에 근거한 가정으로, 한 모체로부터 나오는 자손의 수를 상수 r로 일정하다고 하는 가정이다. 즉,
이다. 이때 r을 증가율, 혹은 증가 속도라고 한다. 방정식 (2)의 양 변을 적분하면
를 얻는다 (단, b(0)는 시각 t=0에서의 출생 수). 이 식을 변형하면, b(t)=b(t-a)era가 주어지고, 양 변에 e-ra를 곱하면
와 같이 주어진다. 식 (3)를 식 (1)에 대입하면,
이므로, 양 변에 b(t)를 약분하면
을 얻는다. 이때, 식 (4)을 Lotka-Euler 방정식의 연속형이라고 한다.
2.2.2 기초감염재생산수의 추정식 유도
다음으로, 2.2.1절에서 유도된 Lotka-Euler 방정식을 이용하여 감염재생산수를 표현하는 방법에 대해 설명한다. 만약 b(t)를 시각 n(a)에서의 신규 감염자 수라고 하고, a를 감염기(infectious period) R(0) 시간째의 감염자가 감염시킬 수 있는 사람의 수라고 하면, n(a)의 정의에 따라 감염자가 감염기 동안 감염시킬 수 있는 총 환자의 수는 a를 모든 에 대해 다 합하면 된다. 즉,
이다. 한편 n(a)를 ∫∞0n(a)da로 나누면, 이는 확률 밀도 함수(probability density function)이 된다. 이것을 g(a)라 두면,
이므로
의 관계식을 얻는다. 감염 세대 시간(generation time)이란, 한 개인의 감염으로부터 그 개인에 의한 2차 감염까지의 시간을 의미한다 (2.2.4절 참조). 앞 절에서 유도된 Lotka-Euler 방정식에서 ‘연령 a’를 ‘감염기 시작 후 a시간’으로 본다면, g(a)는 개인의 감염기 시작 후 그 개인에 의한 2차 감염까지의 시간에 대한 확률 밀도 함수가 되므로, 이는 세대 시간 분포(generation time distribution)이 된다. 식 (6)을 식 (4)에 대입하면,
가 된다. 이때, 식 (7)의 우변은 확률 밀도 함수 g의 적률 생성 함수(moment generating function)의 형태와 같다. 확률변수 T의 확률 밀도 함수가 g일 때, 확률변수 T의 적률 생성 함수는
와 같이 정의 되므로 (단, E(X)는 확률변수 X의 평균), 식 (7)은
와 같이 변형되고, 양 변에 역수를 취하면
와 같이 표현된다. 즉 감염병의 증가 속도 r에 대한 추정값(estimate) r과 감염 세대 분포 T의 확률 밀도 함수를 알면 R0에 대한 추정량(estimator)R0는
이다. 감염 세대에 대한 확률분포 T가 각각의 분포를 따를 때, R0에 대한 추정식은 1 과 같다.
Table 1.
Estimators based on the distribution of generation time (serial interval)
2.2.3 감염병의 증가율(growth rate) r 추정
1) 결정론적 모델(deterministic model)을 이용한 감염병의 증가율(growth rate) 추정: 먼저, 결정론적 모델로써 선형 출생 모델 (Malthusian model)을 소개한다 (Chowell, 2017). 시간 t에서의 확진 수(incidence)에 대한 미분가능한 함수 i(t)에 대하여 일별 환자 발생수의 변화율 (di(t)/dt)이 각 시간에서의 환자 수에 비례한다고 하자. 즉,
이고 (단, 는 x(t)의 시간 t에서의 미분계수), 이는 비례상수 r를 이용하여
와 같이 표현할 수 있으며, 이 식은 초기시간 t=0에서의 확진자 수 i(0)=i0가 주어졌을 때
로 식 (2)와 같이 나타내어진다 (Chowell, 2017). 이때 r은 감염병의 증가 속도이다. r>0이면 시간 t에서의 확진 수의 변화율이 양수이므로 시간 t에서의 확진 수 i(t)는 증가하며, r<0인 경우는 시간 t에서의 확진 수 의 변화율이 음수이므로, 확진 수 i(t)는 감소하며, r=0인 경우는 확진 수의 변화율이 0이고 시간 t에서의 확 진 수가 변화하지 않으므로 확진 수는 유지된다
(모델 1)을 이용하여 t=0(일)에서 t=T(일)까지의 일별 확진 수 데이터 i0Data, i1Data, ···, iTData에 대하여, 최소 제곱법 (method of least squares)을 이용하여 r의 값을 추정한다. 결정론적 모델 (모델 1)로부터 추정되는 증 가속도의 추정량 r 1 ^
로 주어진다. 추정되는 모수(parameter)의 불확실성(uncertainty)를 정량화하기 위해 각 시점에서 시계열 데이터 itData을 평균으로 하는 포아송 분포(Poisson distribution)을 따른다고 가정하여 1000번의 반복 관측치를 추 출하는 부트스트랩 방법을 이용하였다 (Chowell, 2017).
2)확률론적 선형 출생 모델(Stochastic linear birth model)을 이용한 증가율 추정: 확률론적 선형 출생 모델로서 Yule-Furry process를 소개한다(Allen, 2010; Leld et al., 2019). Yule-Furry의 확률과정은 출생 모델(pure birth process)이라고도 불리며, 연속시간 마코프 체인 과정(Continuous time Markov chain, CTMC)이다. C(t)를 시간 t에서의 인구라고 하자. C(t)=n일 때, C(t+∆t)=j일 확률은
로 주어지는 확률과정을 Yule-Furry process라고 한다. 이때 r은 증가 속도이다.
이제, 시간 0에서의 초기 인구가 C0일 때, t시간 후의 인구 Ct가 n명일 확률, 즉, 시간 t까지 n-C0명의 출생이 이루어졌을 확률 ℙ (Ct=n∣C(0)=C0을
라고 정의하자. 그러면, t+∆t시간에서 인구가 n명일 확률은, t시간에서 인구가 n명이면서 생산이 이루어지지 않는 경우의 확률과, t시간 인구가 n-1명이면서 생산이 이루어진 경우의 확률의 합으로 표현할 수 있으므로, (모델2)에서
로 표현이 된다. (11)을 전개하여 양 변을 ∆t로 나누면,
가 되고 양 변에 ∆t→0의 극한을 취하면, 아래와 같은 콜모고로프의 전진방정식(Kolmogorov's forward equation)
을 얻는다 (단, pC0(0)=1, pn(0), n≠C0) (Allen, 2010). 이 식을 풀기 위해서는 확률 생성 함수 방법 (method of probability generating function)을 이용한다 (Allen, 2010). CTMC{C(t) ∣ t∈ [0,∞)}의 확률 생성 함수 P를
라고 하자. 그리고 식 (12)의 양 변에 zn를 곱하고, n=0에서부터 ∞까지의 합을 취해주면
와 같이 주어진다 (단, P(z,0)=zC0이고, ∂ P ( x , y ) ∂ x
z= exp θ의 변수변환을 통해
의 적률 생성 함수로 표현되고, 식 (13)은
로 변환된다. 이제 편미분방정식 (14)를 풀기 위해 특성함수 방법(method of characteristics)을 이용하면 (Strauss, 2007), 적률 생성 함수 M(θ,t)는
과 같이 계산되고, 앞에서 변수변환 관계식 z= exp(θ)의 양변에 로그를 취해 θ=ln z를 대입하면 확률 생성 함수 P(z,t)는
인데, 이는 음이항분포(negative binomial distribution)를 생성하는 확률 생성 함수이다 (Downton et al., 1961). 따라서,
가 된다. 여기서 i+C0=n으로 변수변환 하고,p=exp (-rt)와 q=1-exp (-rt)를 대입하면, 아래와 같이 표현된다.
따라서, 식 (15)로부터
로 표현되므로,
이다. 상수를 곱하는 것은 최대와 최소를 구하는데 아무런 영향을 끼치지 않으므로, 우도(likelihood) L은
이다 (Nishiura et al., 2009).
우도 L을 최대로 하는 r을 추정하는 것은, -ln L을 최소로 하는 r을 추정하는 것과 동치이므로 (Downton et al., 1961), 확률론적 모델 (모델 2)로부터 추정되는 증가 속도의 추정량 r 2 ^
로 추정한다. (10)과 (16)의 추정값을 구하기 위해 각각 MATLAB 내장함수 lsqnonlin과 fmincon을 이용하였 다.
2.2.4 Serial interval의 분포
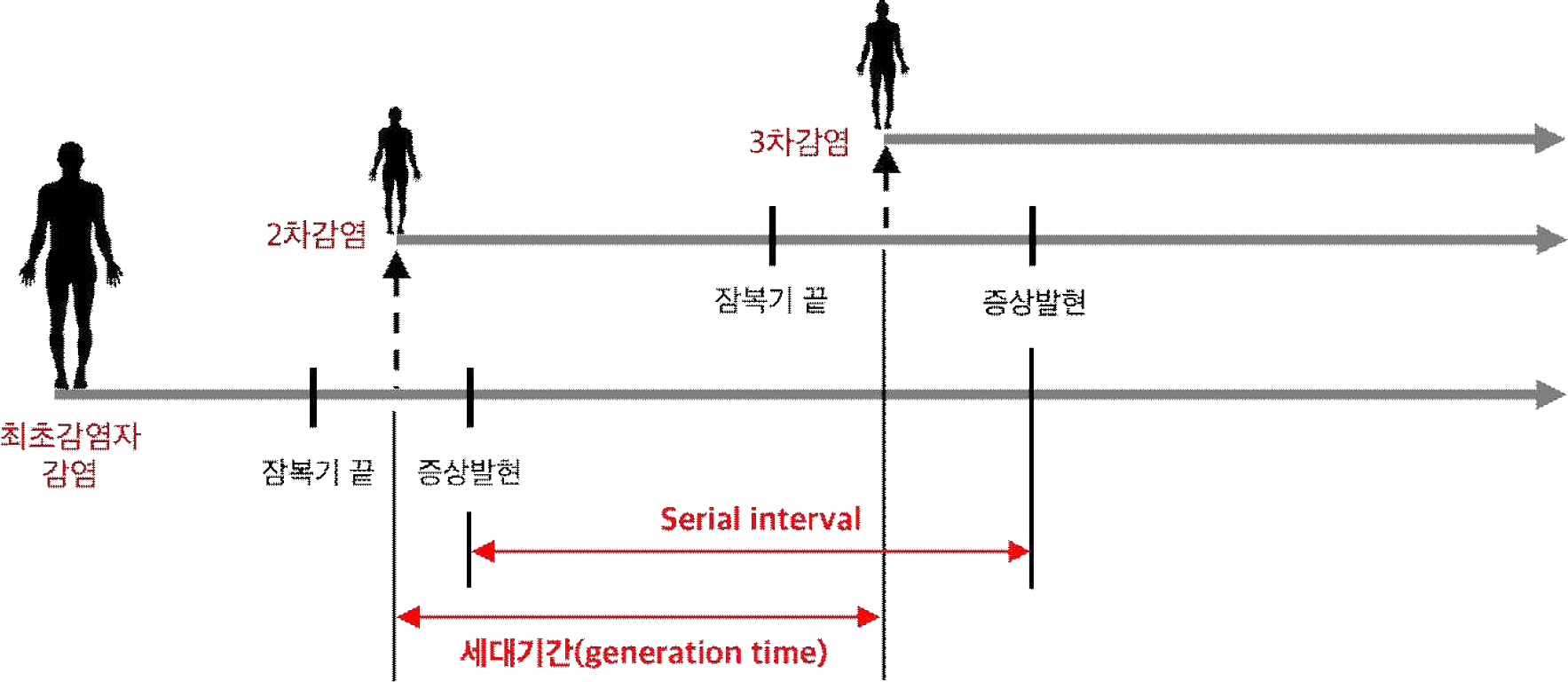
감염병 전파의 초기단계에서는 감염기간(infectious period)이나 잠복기(incubation period), 잠재기(latent peri-od)같은 자료들이 존재하지 않는다. 따라서 세대 기간(generation time)만을 이용하여R0를 산출함을 알고 있다 (Wallinga et al., 2007). 한편, 감염기간은 관찰 불가능한 시간이므로, 우리는 serial interval을 대체하여 사용한다 (Roberts and Heesterbeek, 2007). Serial interval이란, 첫 감염병 발생자의 최초 증상 발현 시점과 2차 감염자의 최초 증상 발현 시점 사이의 시간 차이를 말하며, 관찰 가능한 값이다 (Figure 1; Milwid et al., 2016; Roberts and Heesterbeek, 2007).
한편, 대한민국에서 코로나-19의 경우 serial interval에 대한 정보가 부족한 상황이다. 따라서 중국의 사례를 가지고 연구된 세 편의 논문을 바탕으로 Serial interval의 분포는 평균이 4.5일, 표준편차가 3.1일, 즉, 변동계수가 0.69인 감마분포를 따른다고 가정하였다 (Zhuang et al., 2020).
이 경우, 표 1 에 의해 (모델 1)로부터 얻어지는 R0의 추정치 R 0 1 ^
이며, (모델 2)로부터 얻어지는 R0의 추정치 R 0 2 ^
이다. 우리는 (모델 1)과 (모델 2)를 동일한 가중치의 부여한 추정치인 R 0 ^
로 정의하고 이를 바탕으로 감염재생산수를 분석하였다. 우리는 두 모델의 가중치를 동일하게 ω1=ω2=0.5로 두고 감염재생산수를 추정하였다.
2.2.5 실질감염재생산수의 추정식 유도
기초감염재생산수는 질병의 초반 기하급수적 증가를 따르는 데이터에 대해 추정되었다면, 실질감염재생산수는 각 감염 세대별로 감염재생산수를 추정한다. 세대 기간의 분포는 2.2.4절에서 사용 된 것과 동일한 분포를 사용하였다. Nishiura et al.(2010)에서 제시된 이상적인 추정 단위기간(ideal reporting interval)은 serial interval이라는 사실 을 이용하여 평균 4.5일을 반올림한 5일을 한 세대의 길이로 정의하고, 5일 간격(세대 간격)으로 Rt를 추정하였다. 각 감염 세대별 감염병의 증가속도 rk를 추정하기 위해, 각 감염 세대별 최초 확진자(initial incidence) ik를 가정하여, 질병은 기하급수적 증가를 따른다고 가정한다. 따라서, 감염 세대별 확진자 데이터를 이용하여 각 세대별 감염병의 증가속도 rk(k 세대의 감염병 증가속도, k= 1, 2, ⋯, m)를 2.2.3절에서 유도된 식 (10)을 이용하여 추정한다. 즉,
이고, 각 세대별 감염재생산수 Rk는 추정된 각 세대별 증가속도 r k ^
와 같이 추정한다. 그리고 각 세대별로 추정된 m세대에 대한 감염재생산수
들의 모임을 Rt로 정의한다.
3.국내 코로나바이러스감염증-19의 감염재생산수 추정
3.1 데이터
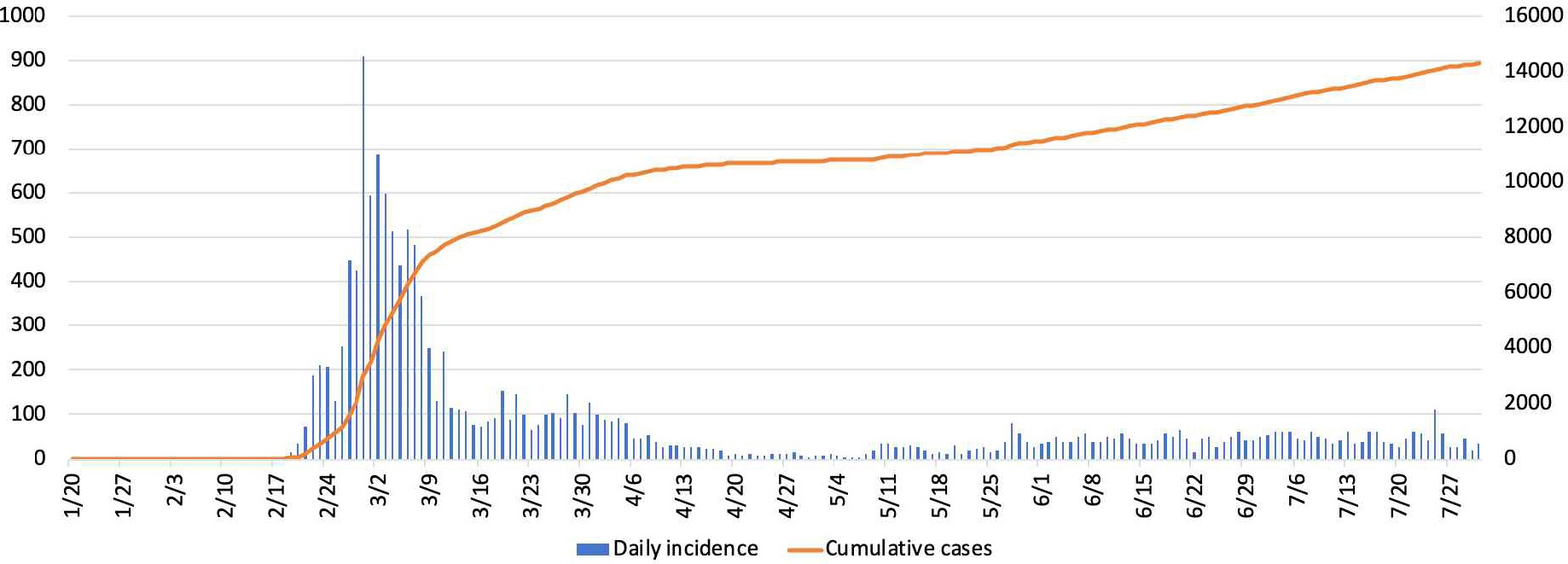
본 연구에서는 코로나-19의 감염력을 분석하기 위해 질병관리본부 홈페이지에서 제공하는 2020년 8월 1일 0시 기준의 공공데이터를 사용하였다 (MOHW, 2020). 이 자료에는 누적발생 현황, 지역별 현황, 확진자의 성별, 연령별 현황 등의 자료를 포함한다. 본 연구에서는 코로나-19의 감염력이 연구의 대상이므로 감염력의 속도를 파악하는 주요 값인 신규 확진자 수를 중심으로 연구를 수행하였다. 사용된 데이터의 해당 기간은 2020년 1월 20일부터 2020년 7월 31일이며, 2월 29일까지의 데이터는 오전 9시, 오후 16시 기준의 데이터가 제공되었기 때문에, 당일의 신규 확진자수는 익일 오전 9시 기준의 데이터로 취급하였다.
Figure 2 의 왼쪽범례는 일별 확진자 수, 오른쪽 범례는 누적 확진자 수를 나타낸다. 첫 확진 자 발생일인 1월 20일부터 2월 18일까지 최초 30일간은 일별 신규 확진자수 가 5명 이하로 안정적으로 유지되었지만, 2월 19일을 기점으로 하여 일별 신규 확진자는 기하급수적 증가의 양상을 보였다. 2월 29일에 일별 확진자가 기록 최댓값인 909명을 기록한 후 신규확진추이는 점차 감소세로 전환되었다. 2월 29일 이후 돌발적으로 확진추이가 증가하는 양상을 보이 기도 하였지만 5월 초까지 대체적으로 감소하는 추세를 보이고 있다가. 이후 일별확진자가 30-50명순에서 유지되고 있다.
3.2 기초감염재생산수의 추정
감염재생산수는 2020년 1월 20일부터 보고된 누적 확진 환자 수에 대한 시계열 데이터를 통해 추정하였다. 그러나 2020년 1월 20일부터 초반에서의 확진자수는 일정한 패턴을 보이지 않으므로, 질병이 국내에서 유행한 것이 1월 20일이 아니라고 가정하였다. 1월 말에서 2월 초에 청도 대남병원에 다녀온 신천지 환자들이 특별히 집단 감염을 일으킨 31번 환자의 신천지 예배일이 2월 9일이다. 따라서 우리는 1월 말에서 2월 초에서 평균 잠복기인 4-5일이 지났으며, 신천지 예배가 있었던 2월 9일 이전인 2월 4일에서 6일 사이를 질병 전파의 시작일이라고 가정하였고, 아래의 세 가지 시나리오
에 대해 감염재생산수를 추정하였으며, 기하급수적 증가를 보이는 2020년 2월 29일까지의 데이터로 추정하였다. 2 는 (모델1)에서부터 유도된 (1)과 (모델2)에서부터 유도된 (7)를 최소화하는 추정된 증가율 r과 (10)로부 터 추정된 를 나타낸다. 세 가지 시나리오를 가정하여 두 모델을 산술평균하여 추정한@@@는 약 3.1 (3-3.2)의 값을 가진다. 이는 기존의 연구의 1.5(Shim et al., 2020(2)), 1.77(Kim et al., 2020)보다 확연하게 다른 결과인데, 질병의 최초 발생을 1월 중순으로 보지 않고, 31번 확진자의 확진일 근방인 2월 초로 설정하였기 때문이다.
Table 2.
Estimated growth rate and basic reproduction number using each model against three scenarios
Figures 3–5 는 각각 Scenario 1, 2, 3에서 (모델1)과 (모델2)의 모수 추정 결과로부터 구현된 시계열 모델 표현이다. (모델1)의 결과는 연속시간 마코프체인(Continuous time Markov Chain) 시뮬레이션 방법의 일종인 Gillespie의 시뮬레이션 방법으로 구현된 결과이며 (Higham, 2008), (모델2)의 결과는 각 시점의 데이터에 대해 포아송 에러를 가정한 부트스트랩 방법을 이용하여 1000번의 독립적 시뮬레이션을 바탕으로 얻은 결과이다 (Chowell, 2017). 파란색 실선은 평균, 빨간색 점선은 95% 신뢰구간, 동그라미는 실제 데이터를 나타낸다. 이를 통해 두 모델이 시계열 데이터를 잘 표현하는 모델이라는 것을 알 수 있다. 추정된 는 시나리오에 따라 편차를 가지는데 결정론적 방법으로 추정된 방법에서는 0.23의 편차를 가지며, 확률론적 방법으로 확률론적 방법으로 추정된 방법에서는 0.02의 편차를 가진다. 지금까지 알려진 감염병 중 비말을 매개로 하는 사스바이러스의가 2~5, 인플루엔자 바이러스의 가 2~3인 점과 비교해보면 (WHO, 2020), 코로나-19의 전파속도는 위협적이라 할 수 있다.
Figure 3.
Fitted trajectories of cumulative cases with Model 1(left panel) and Model 2(right panel) versus time of Scenario 1, respectively. Circled dots represent real data. Blue line represents median and 95% credible interval ranges are shown as dashed red line. Whole results are shown in grey line.

Figure 4.
Fitted trajectories of cumulative cases with Model 1(left panel) and Model 2(right panel) versus time of Scenario 2, respectively. Circled dots represent real data. Blue line represents median and 95% credible interval ranges are shown as dashed red line. Whole results are shown in grey line.
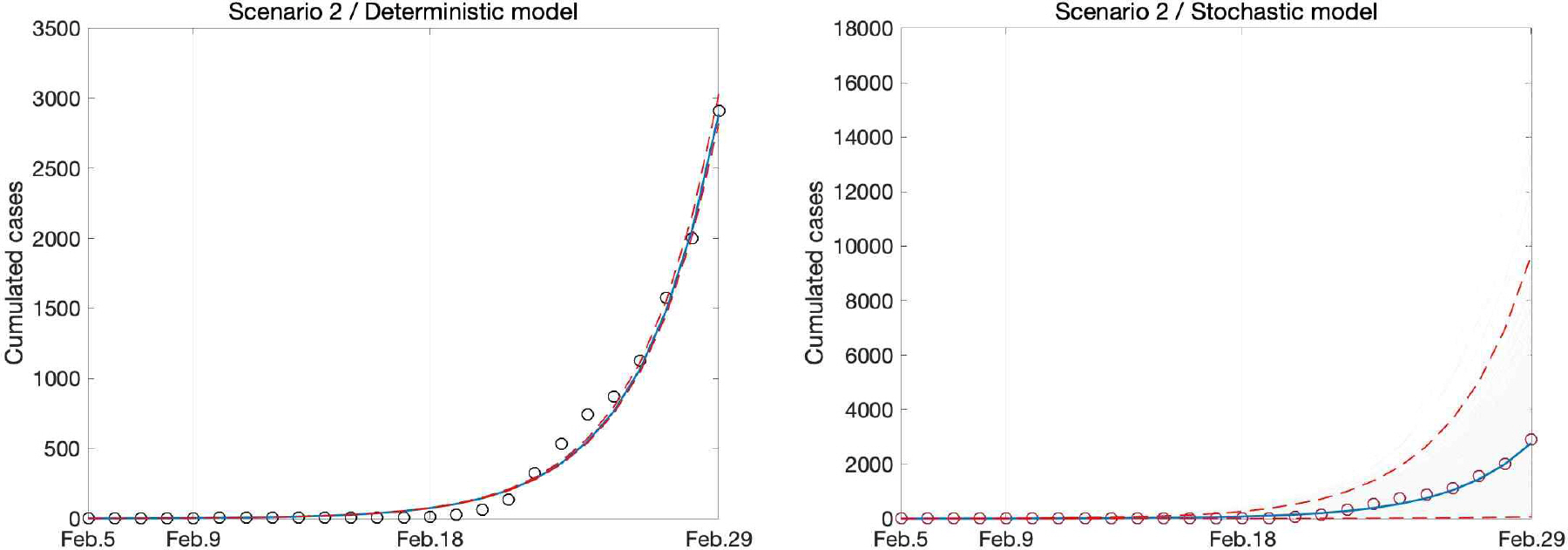
3.3 실질감염재생산수의 추정
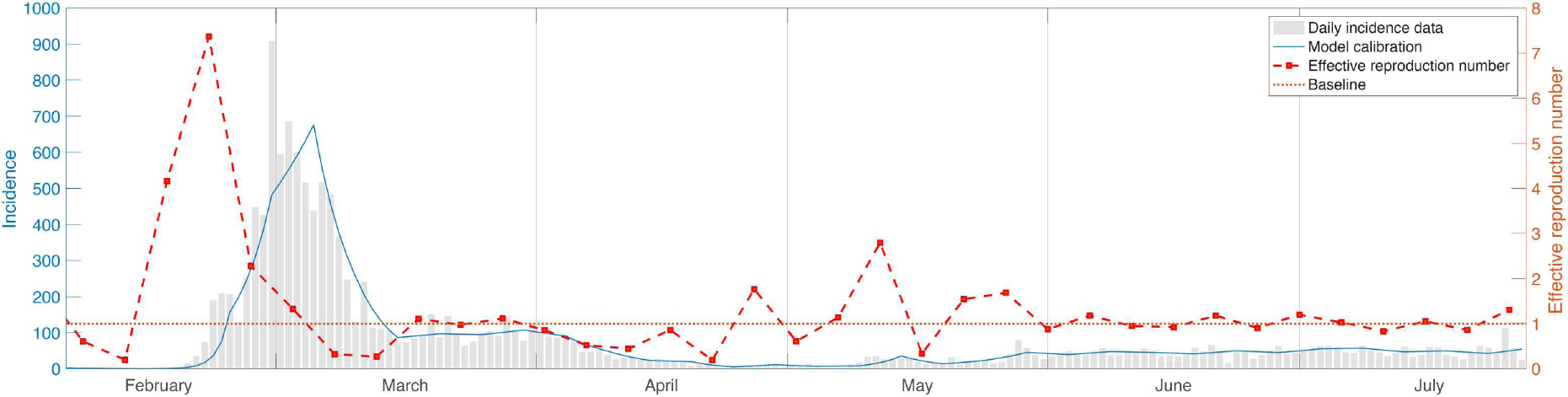
실질감염재생산수는 2020년 1월 20일부터 2020년 7월 31일까지의 대한민국에서의 보고된 누적 확진환자수에 대한 시계열 데이터를 통해 추정하였다. Figure 6 은 5일 간격으로 Rt를 추정한 결과를 나타낸다. 2월 15일에 추정된 R t ^
3.4 정부의 대응
실질감염재생산수는 후행지표로써 이를 이용하여 정부의 대응을 평가하는데 도움을 줄 수 있다. 3 은 시기별로 시행된 보건당국의 코로나-19 주요 대응 정책을 나타낸다. 이를 실질감염재생산수를 나타내는 Figure 6 을 살펴보면, 2월 하순 급격한 증가 추세 이후 감염병이 안정적으로 관리되고 @@@가 1 미만의 값으로 유지 되는 데에는 2020년 2월 12일부터 시행된 마스크 사용 권고 조치, 입국제한조치 및 중앙재난안전대책본부 설치 등의 범정부적 대응강화, 개학연기와 같은 정부의 보건정책의 효과가 발휘된 것으로 추정된다. 그러나 5월부터 2020년 5월 14일 현재까지는@@@가 1을 초과하는 다시 증가하는 모습을 보였다. 이는 이태원 클럽의 집단감염에 기인하는데, 이는 완화된 사회적 거리두기의 시행으로 인한 감염병에 대한 사회적 경각심 감소, 2020년 4월 30일부터 2020년 5월 5일까지의 어린이날을 포함하는 이른바 ‘황금연휴’ 기간의 여행 등의 이동수요 증가로 사회적 거리두기 조치의 유효성 감소가 원인인 것으로 추정된다. 이후 6월부터는 @@@가 다소 증가하여 1 근방에서 유지되고 있음을 볼 수 있다. 이를 통해 완화적 사회적 거리두기 정책이 감염병의 폭발적인 확산방지에는 효과적으로 기여하고 있으나, 질병의 종식의 목표달성에는 다소 아쉬운 정책으로 보인다.
Table 3.
Government responses for COVID-19 control.
4.결 론
본 논문에서 대한민국 내 코로나-19의 감염력 분석을 위한 확진자 데이터 분석 및 감염재생산수의 추정에 대한 연구를 수행하였다. 제2절에서는 연구 수행을 위한 구체적 연구방법으로써 기초감염재생산수, 실질감염재생산수의 개요와 구체적 추정방법에 대해 기술하였다. 본 연구에서는 감염재생산수의 추정을 위해 구체적인 모델로써 인구 증 가를 설명하는 모델인 선형출생모델을 사용하여 결정론적 방법과 확률론적 방법으로 감염재생산수를 추정하였다.
본 연구에서 추정한 기초감염재생산수는 약 3.1(3-3.2) 수준이다. 코로나-19가 폭발적으로 유행시킨 슈퍼확진자로 평가되는 31번 환자의 감염일을 평균 잠복기를 고려하여 질병 전파 시작일을 세 가지 시나리오로 구분하였고, 구분된 시나리오를 바탕으로 결정론적 방법과 확률론적 방법으로 선형출생모델을 활용한 기초감염재생산수를 추정하였다. 추정된 기초감염재생산수는 선행연구에서 추정된 값과 대체적으로 유사하였다. 추정된 기초감염재생산수 3(2.99~3.22)는 지금까지 알려진 비말을 매개로 하는 감염병인 사스와 인플루엔자와 비슷하거나 다소 높은 수치임을 고려할 때, 코로나-19의 감염력 및 위험도가 대단히 높은 질병임을 나타낸다.
또한 실질감염재생산수의 시계열 추정으로 3월 이후의 보건당국의 보건정책은 대단히 효과적이었음을 확인하였다. 다만, 선제적인 보건정책의 부재로 2020년 2월 18일 이후 폭발적인 증가태세를 막지 못한 것에 대한 아쉬움이 있다. 또한 5월 이후 현재까지 감소세에 있던 신규확진자수는 산발적 소규모 집단감염의 발생으로 증가추세에 있는데, 2020년 3월 22일부터 2020년 4월 19일까지 시행된 고강도 사회적 거리두기 정책이 국가경제 등에 부담이 된다는 이유로 완화된 사회적 거리두기(2020년 4월 20일), 생활 속 거리두기(2020년 5월 6일)로 다소 이른 시점에 전환된 점 또한 대단히 아쉽다. 추후 보건당국의 정책결정에 있어 전염력 분석 등을 활용한 선제적이고 효과적인 보건정책의 시행이 필요해 보이며, 또한 이를 위해 감염병 관련 정책결정에서 정치논리에 의한 의사결정보다는 전문성을 가진 질병관리본부의 질병 정책 컨트롤타워로써의 권한확대가 필요해 보인다. 이러한 관점에서 현재 논의되고 있는 질병관리본부의 질병관리청 승격은 반가운 소식이다.