서울시 초미세먼지(PM2.5) 지역별 극단치 분석
Abstract
Purpose
This paper aims to investigate the concentration of fine particulate matter (PM2.5) in the Seoul area by predicting unhealthy days due to PM2.5 and comparing the regional differences.
Methods
The extreme value theory is adopted to model and compare the PM2.5 concentration in each region, and each best model is selected through the goodness of fitness test. The maximum likelihood estimation technique is applied to estimate the parameters of each distribution, and the fitness of each model is measured by the mean absolute deviation. The selected model is used to estimate the number of unhealthy days (above 75μg/m3 PM2.5 concentrations) in each region, with which the actual number of unhealthy days are compared. In addition, the level of PM2.5 concentration in each region is analyzed by calculating the return levels for periods of 6 months, 1 year, 3 years, and 5 years.
Results
The Mapo (MP) area revealed the most unhealthy days, followed by Gwanak (GW) and Yangcheon (YC). On the contrary, the number of unhealthy days was low in Seodaemun (SDM), Songpa (SP) and Gangbuk (GB) areas. The return level of PM2.5 was high in Gangnam (GN), Dongjak (DJ) and YC. It will be necessary to prepare for PM2.5 than other regions. On the contrary, Gangbuk (GB), Nowon (NW) and Seodaemun (SDM) showed relatively low return levels for PM2.5. However, in most of the regions of Seoul, PM25 is generated at a very poor level (75μg/m3) every 6months period, and more than 100μg/m3 PM2.5 occur every 3 years period. Most areas in Seoul require more systematic management of PM2.5.
Conclusion
In this paper, accurate prediction and analysis of high concentration of PM2.5 were attempted. The results of this research could provide the basis for the Seoul Metropolitan Government to establish policies for reducing PM2.5 and measuring its effects.
Key words: Air Quality, Fine Particulate Matter (PM2.5), Extreme Value Theory (EVT), Generalized Extreme Value (GEV) Distribution, Generalized Pareto Distribution (GPD), Return Period, Return Level
1. 서 론
산업 전반에 걸쳐 대기오염이 전 세계적으로 큰 영향을 끼치고 있다. 세계 도시인구의 80% 이상이 기준치를 넘는 대기오염에 노출된 것으로 평가되고 있으며, 대기오염물질 중 미세먼지(PM10, PM2.5)는 매년 3백만 명 이상의 조기사망을 일으키는 원인으로 지목되고 있다( WHO 2016). 특히 한국은 초미세먼지로 인해 연간 18,200명이 사망하는 등 대기오염이 심각한 수준이며, 대책을 마련하지 않는다면 2060년 OECD 회원국 중 조기사망률 및 경제적 피해가 가장 클 것이라 전망되었다( OECD, 2016). 또한, 중국에서 발생한 대기오염이 한국으로 장거리이동을 하면서, 2012년 기준으로 매년 우리나라의 11,523명이 조기사망하고 있는 등 국민건강에 큰 위협을 끼치고 있다( Zhang et al. 2017). 이처럼 대기품질 문제는 단순한 작은 피해수준이 아니라 국내·외에서 재해수준으로 부상하고 있다. 이러한 상황으로 인해 최근 우리나라 대기오염의 원인을 파악하고 대기품질을 향상시키기 위한 다양한 연구가 진행되고 있다. 특히, 중국의 황사 및 스모그가 우리나라에 대기질에 큰 영향을 미친다는 연구가 보고되고 있으며( Kim et al. 2016), 최근에는 중국에서 생성된 초미세먼지(PM2.5)로 인해 우리나라와 일본의 조기 사망자가 3만 여명에 달한다는 연구도 발표되었다( Zhang et al. 2017). 또한, 환경부는 중국뿐만 아니라 국내의 공장, 자동차 등 배기가스, 도로, 건설현장, 산불 등의 영향도 크며, 2012년 기준으로 PM10은 119,980톤, PM2.5는 76,287톤가량이 배출되었다고 발표하였다( 국립환경과학원, 2012). 또한, 최근에 서울시는 2015년 8월~2016년 4월까지 수도권의 PM10과 PM2.5의 국내 배출 영향이 45%, 외부지역(중국, 북한, 그 외) 배출 영향이 55%를 차지한다고 발표(서울특별시 2016)하는 등 국내의 요인도 상당수 차지한다는 연구가 진행되었다. 이처럼 우리나라는 국내 및 국외로부터 발생한 대기오염물질의 영향으로 건강과 경제적으로 심각한 위기에 처해 있다. 이러한 초미세먼지 피해에 대해 리스크를 측정하고 대책을 마련하기 위해, 해외에서는 극단치 이론(Extreme Value Theory; EVT)을 적용한 미세먼지 리스크 분석 및 모델링이 연구되고 있다. Gavin 등(2017)은 전 세계의 미세먼지 분석을 수행하기에는 자료를 모니터링하는데 한계가 있다는 것을 설명하며, 위성, 지역 모니터링, 기타 등에서 미세먼지 데이터를 구하고 이를 통합하여 분석하는 기법을 개발하였다. 통합된 데이터로 미세먼지 현황을 보여주었는데, 동아시아 지역이 특히 농도가 높고 극단치를 보여주는 지역으로 나타났다. Amin et al(2013)은 미세먼지 농도에 경향이 보이는 말레이시안 지역에 베이지안 기반의 비정상성 (non-stationary) 극단분포를 이용하여 모델링하는 것을 보여주었다. Battista et al(2016)은 로마지역의 미세먼지 등의 대기오염 수준의 평가를 위해 극단치분포를 사용하였다. 또한, Ahmat et al(2015)은 말레이시아 지역의 고농도 미세먼지 발생에 대한 정확한 추정을 위해 극단치분포를 사용하였다. 국내에서도 EVT를 사용하여 미세먼지 영향을 분석한 연구를 살펴볼 수 있다. Park et al(2017)은 일반화극단치분포(Generalized Extreme Value; GEV)를 사용하여 서울시 미세먼지(PM10) 자료의 시간 및 공간 구조를 분석하였고, 12개월 주기의 재현수준(return level)을 구하였다. 하지만 국내에서 아직까지 초미세먼지 농도에 대해 극단치이론을 적용하여 모델링하고 리스크를 분석하는 연구는 부족한 실정이다. 따라서 본 연구에서는 EVT를 활용하여 우리나라 서울의 행정구역(구별) 단위로 초미세먼지(PM2.5)의 위험일수 추정 및 리스크를 분석하고, 지역별 대책 마련에 근거가 되고자 한다. 2장에서는 분석방법 및 초미세먼지 리스크 분석을 위한 EVT에 대해 살펴보고, 3장에서는 지역별로 극단치분포를 적용하고 최적의 모형을 선정하였으며, 선정된 모형을 통해 위험일수를 추정하고 리스크 분석을 진행하였다. 4장 결론에서는 분석 결과에 대한 요약 및 추후 연구방향을 정리하였다.
2. 연구방법
2.1 데이터 및 분석 도구
본 논문의 서울시 지역별 PM2.5 데이터는 에어코리아에서 제공하는 국립환경과학원의 최종확정자료를 활용하였다. 분석 기간은 PM2.5의 농도가 공개된 시점으로부터 발표된 최종확정자료인 2014년 1월 1일~2018년 6월 30일까지이며, 초미세먼지가 관측되지 않은 결측치(missing value)에 대해서는 제거하고 분석을 진행하였다. 또한 EVT에서는 일반적으로 최대치(maxima)를 활용하나, 본 논문에서는 일시적인 최대치보다는 PM2.5의 지속시간을 고려하기 위해 일일 평균(daily-mean) 데이터로 분석을 진행하였다. 분석 도구로는 주로 R을 활용하였으며, 데이터 전처리에서 excel도 함께 사용하였다. EVT를 적용하기 위해 사용한 R 패키지는 evd이며 데이터 전처리, 그래프 등의 처리를 위해 dplyr, ggplot2패키지를 사용하였다. 사전에 지역(행정자치구)별로 분석한 기본 통계량은 Table 2와 같다.
2.2 확률분포 추정 및 최적 모형 선정
서울시 각 지역구의 PM2.5 농도에 대한 개략적인 현황을 살펴보고자 상자 그림을 도식하여 나타내었다. 국내 일평균 기준(35μg/m3)으로 살펴보면, 서울시의 모든 지역에서 PM2.5 농도의 평균 및 3분위수까지는 기준치 이하로 나타나고 있다. 하지만 국내 기준치를 초과하는 다수의 극단치가 나타나고 있어 서울시의 각 지역은 고농도의 PM2.5에 빈번하게 노출되고 있음을 유추할 수 있다. 따라서 서울시의 PM2.5를 제대로 진단하고 모델링하기 위해서는 극단치를 반영할 수 있는 분포가 필요하다. 참고로 각 지역의 PM2.5는 평균적으로 WHO 일평균 기준(25μg/m3)과 유사하게 발생하고 있어 추후 WHO 권고기준을 준수하기 위해서는 전반적인 PM2.5의 저감이 필요하다.
2.2.1 극단치이론(Extreme Value Theory)
극단치이론(EVT)은 어떤 사건이 희박하게 발생하지만 영향이 매우 크거나 아주 작은 사건의 리스크를 분석하여 주요한 의사결정을 지원하는데 유용한 이론이다. 통계적으로 리스크를 제대로 측정하기 위해서는 확률분포에서 꼬리 영역에 관심을 두어야하고, 이는 극단치의 움직임에 초점을 맞추는 것이 필요하다( D. K. Dey and J. Yan. 2016). 본 논문에서는 Weibull, GEV, GPD 등의 분포를 사용하여 서울의 지역별 초미세먼지 농도를 모델링하고 최적의 모형을 선별한다. 특히, Figure 1과 같이 빈번하게 발생하는 극단치를 반영할 수 있는 분포로써 GEV, GPD 분포를 고려하였다. 해당 분포들의 PDF와 CDF를 Table 3에 정리하였다. 극단 사건의 분석에 있어서, 언제 그 사건이 발생하는지(재현주기; return period)와 그 사건이 얼마나 크게 나타나는지(재현수준; return level)가 매우 중요하다. 재현수준은 데이터의 주기(1/ p)에 따라 식 (1)의 p를 변화시켜가면서 계산할 수 있다.
2.2.2 최적 모형 선정
각 모형의 적합도를 비교하고 최적 모형을 선별하기 위해 다음의 식 (2)와 같이 MAD(Mean Absolute Deviation)을 활용하였다. MAD는 실제로 관측된 값의 선험적(Empirical) CDF와 모수적 모형으로 추정된 CDF 값의 절대 편차(absolute deviation)를 적분하고 표본크기 n으로 나누어 구할 수 있다.
F*(x): 선험적 CDF, F^(x): 모수적 (극단치) 모형으로 추정된 CDF
위에서 설명한 PM2.5 데이터와 분석 기법을 활용하여, 최적의 분포를 선정하고 정확한 위험일수를 추정하기 위한 절차를 Figure 2와 같이 요약할 수 있다.
3. 서울시 초미세먼지(PM2.5) 농도 데이터 분석
3.1 지역별 초미세먼지(PM2.5) 농도 모형 추정
지역별 PM2.5 모형을 비교하기 위해 MLE 기법으로 각 분포의 모수를 추정하고, 진단그림(diagnostic plot)을 통해 모형의 적합도를 살펴보았다. 진단 그림에서는 ‘P-P plot’, ‘Q-Q plot’, ‘Density Plot’, ‘Return Level Plot’ 등 네 가지를 살펴볼 수 있으며, 예시로 동작구 지역의 GEV, GPD 진단그림을 Figure 3에 나타내었다. 동작구 지역의 예시에서는 각 ‘Q-Q Plot’과 ‘Return Level Plot’에서 시각적인 차이를 발견할 수 있는데, 각 Plot의 끝부분을 살펴보면 GEV모형이 GPD모형보다 더 적합한 분포임을 유추해볼 수 있다. 동작구의 예시처럼 다른 24개 지역도 마찬가지로 각 분포의 모수를 추정하고 진단 그림을 통해 모형의 적합함을 일차적으로 확인하였다.
3.2 적합도 검정
서울 지역구별 최적의 모형을 선별하기 위해서 각 지역의 GEV, GPD, Weilbull 모형별 MAD를 계산하고 적합도(goodness of fit)를 비교하였다. 동작구 지역을 예시로 MAD를 계산하면 Figure 4와 같다. Weibull 모형이 0.00266으로 가장 실제의 관측값과 차이가 많이 나고, GEV가 0.00035로 가장 작은 차이로 나타나 GEV를 가장 적합한 모형으로 선정할 수 있다. 동작구 지역의 예시처럼 각 지역의 MAD를 계산하고 최적 모형을 선정하여 모수와 함께 Table 4에 정리하였다. 17개 지역은 GEV 모형이 적합하게 나타났으며, 나머지 8개 지역은 GPD 모형이 더 적합하게 나타났다.
3.3 지역별 위험일수 추정 및 재현수준
3.3.1 지역별 위험일수 추정
각 지역의 위험일수를 추정하기 위해 지역별 최적 모형의 CDF를 통해 국내 PM2.5의 매우 나쁨 기준인 75 μg/m3을 초과하는 확률을 계산하였다. 예를 들면, 도봉구(DB) 지역에서 PM2.5의 농도가 매우 나쁨 수준인 75 μg/m3를 실제로 초과한 일수는 10일이다. 도봉구 지역은 GEV가 최적의 모형이므로 GEV의 CDF로부터 F( x)≤75=0.9949를 얻을 수 있으며, 75 μg/m3를 초과할 확률은 1- F(75) =˙0.0051이다. 따라서 도봉구 지역의 추정 위험일수는 0.0051×909 days=8 days를 계산할 수 있다. 동작구의 실제 위험일수와 추정일수의 차이는 2일로써 상당히 근접하게 추정되었음을 확인가능하다.
실제 위험일수가 가장 높은 지역인 마포 지역의 실제 위험일수는 20일(추정일수 17일)로 나타나 서울지역에서 가장 PM2.5에 취약한 지역으로 나타났다. 관악 지역은 실제 17일(추정 16일)로써 두 번째로 취약한 지역이다. 기준 초과일수가 10일 미만인 지역은 성북(실제 9일, 추정 9일), 강북(실제 8일, 추정 8일), 강서(실제 8일, 추정 9일), 중구(실제 8일, 추정 8일), 서대문(실제 6일, 추정 7일), 송파 지역(실제 6일, 추정 5일)이다.
3.3.2 지역별 초미세먼지 농도 재현수준
지역별로 고농도의 PM2.5의 발생 주기 및 농도 수준을 파악하고자 각 지역의 PM2.5 재현수준을 분석하였다. 6개월, 1년, 3년, 5년 주기로 발생할 수 있는 PM2.5의 지역별 재현수준과 신뢰구간을 Table 6에 나타냈으며, 지역별로 차이를 쉽게 확인할 수 있도록 재현수준 지도를 Figure 5에 도식하였다. 서울 대부분의 지역에서 6개월 주기마다 평균 78.32 μg/m3의 매우 나쁨 수준의 PM2.5가 발생하고 있다. 1년 주기로는 평균 87.88 μg/m3이며, 3년 주기는 평균 102.12 μg/m3의 PM2.5가 발생할 수 있다. 대체적으로 PM2.5의 재현수준이 낮은 지역은 강북(GB), 노원(NW), 서대문(SDM), 송파(SP) 구이며, 재현수준이 높은 지역은 강남(GN), 동작(DJ), 양천(YC) 구로 나타난다.
4. 결론 및 시사점
본 연구는 서울시의 일평균 매우 나쁨 수준(75μg/m3) 이상의 고농도 PM2.5 발생에 대한 정확한 추정을 위해 GEV, GPD, Weibull 분포를 비교하고 최적의 모형을 선정하였다. 모수 추정 기법으로는 MLE를 활용하였으며 지역구별 최적 모형을 선정하기 위한 적합도 판단의 기준은 MAD를 적용하였다.
도봉(DB), 동작(DJ), 은평(EP), 구로(GR), 관악(GW), 성북(SB), 성동(SD), 용산(YS), 영등포(EDP), 강동(GD), 강남(GN), 강서(GS), 중구(JG), 중랑(JR), 서초(SC), 양천(YC) 지역은 GEV 모형이 적합하게 나타났으며, 나머지 광진(GJ), 종로(JN), 마포(MP), 송파(SP), 동대문(DDM), 강북(GB), 노원(NW), 서대문(SDM) 지역은 GPD 모형이 최적의 모형으로 선정되었다. 각 지역구별 선정된 분포를 통해 매우 나쁨 수준인 75μg/m3를 초과하는 위험일수를 추정하고 실제 위험일수와 비교한 결과 상당히 정확하게 나타났음을 확인하였다. 위험일수가 가장 높은 지역은 마포 지역이며, 관악, 양천구 순으로 위험일수가 높게 나타났다. 반대로 서대문과 송파, 강북 지역은 낮은 위험일수를 보였다.
또한, 고농도의 PM2.5의 발생 주기를 파악하기 위해 6개월, 1년, 3년, 5년 주기의 재현수준 및 신뢰구간을 분석하였고, 지역별로 PM2.5 농도의 수준을 쉽게 확인할 수 있도록 재현수준에 따른 지도를 도식하였다. 실제 위험일수가 높은 지역과 마찬가지로 강남(GN), 동작(DJ), 양천(YC) 지역이 PM2.5에 취약한 지역으로 나타났으며, 다른 지역보다도 PM2.5에 대한 대비가 필요할 것이다. 반대로 강북(GB), 노원(NW), 서대문(SDM)은 상대적으로 재현수준이 낮은 지역으로 나타났다. 하지만 6개월 주기마다 서울 대부분의 지역이 매우 나쁨 수준(75μg/m3) 이상의 PM2.5가 발생하고 있으며, 3년 주기로는 100μg/m3을 초과하는 PM2.5가 발생할 수 있어 서울 대부분의 지역이 PM2.5에 대한 관리가 요구된다.
본 연구에서 분석된 서울시 PM2.5의 농도 차이는 지리적 요인으로 원인을 찾아볼 수 있다. 위험일수와 재현수준을 통해 가장 양호한 결과를 나타낸 강북(GB) 지역의 경우, 서북면에 북한산이 위치하여 대기정화 역할을 담당하기 때문인 것으로 해석할 수 있다. 그 인근의 노원(NW)과 도봉(DB) 지역 또한 나쁘지 않은 결과를 나타낸 것을 보더라도 북한산의 효과는 유의한 것으로 판단된다. PM2.5 기준으로 대기품질이 열악한 것으로 나타난 마포(MP)-용산(YS)-강남(GN)으로 이어지는 지역과 양천(YC)-영등포(EDP)-동작(DJ)-관악(GW)으로 이어지는 지역은 공통적으로 북서방면에서 내려오는 라인을 보이고 있다. 즉, 미세먼지를 가장 많이 실어오는 북서풍을 정화시켜 주는 기능이 취약함을 알 수 있다. 서울시를 둘러싸고 있는 그린벨트 가운데 마포(MP)구의 서북 면과 양천(YC)구의 서북 면은 공통적으로 녹지가 부족한 상태이다. 특히, 양천(YC)구는 인근 도시와 바로 연결되어 있어 고농도 재현수준이 높게 나타난 것으로 해석된다.
대기품질은 사람들의 삶의 질을 결정하는 매우 중요한 요소이다. 서울시에서는 대기품질을 개선하고자 미세먼지 농도를 저감하기 위한 다양한 정책을 10여 년 동안 지속적으로 시행하여 왔으나 아직까지 뚜렷한 성과를 거두지 못하고 있다. 이토록 개선하기 어려운 미세먼지 문제는 국민의 건강뿐만 아니라 경제활동 등에도 영향을 끼쳐 사회 전반으로 불이익을 초래하고 있다. 이를 해결하기 위해 지역별 데이터 분석을 통해 자연 공기정화 기능을 극대화 할 수 있는 방안들을 체계적으로 마련해야 할 것이다. 본 논문에서 시도한 PM2.5 농도에 대한 정확한 현 수준의 분석과 예측은 서울시가 정책을 마련하고 그 효과를 측정할 수 있는 기반자료가 될 것으로 기대된다. 추후 연구로서 지리적 요인 뿐 아니라, 계절적, 시간적 요인과 산업적, 환경적 요인 등 다양한 요인을 분석하여 보다 효과적인 대응방안을 제시할 수 있는 연구가 지속되어야 할 것이다.
REFERENCES
Ahmat, H, Yahaya, AS, and Ramli, NA 2015. The Malaysia PM10 analysis using extreme value. Journal of Engineering Science and Technology 10(12):1560-1574.
Battista, G, Pagliaroli, T, Mauri, L, Basilicata, C, and De Lieto Vollaro, R 2016. Assessment of the Air Pollution Level in the City of Rome (Italy). Sustainability; 8(9):838.  Dey, DK, and Yan, J 2016. Extreme Value Modeling and Risk Analysis: Methods and Applications. A Chapman and Hall Book.
Kim, HS, Chung, YS, and Yoon, MB 2016. An Analysis on the Impact of Large-scale Transports of Dust Pollution on Air Quality in East Asia as Observed in Central Korea in 2014,”. Air Quality, Atmos. & Health 9: 83-93.   Mohd Amin, NA, Adam, MB, Ibrahim, NA, and Aris, AZ 2013. Bayesian Extreme Modeling for Non-stationary Air Quality Data. AIP Conference Proceedings 1557(1).  National Institute of Environmental Research 2012. A Study on the Health Impact and Management Policy of PM2.5 in Korea I..
OECD 2016. The Economic Consequences of Outdoor Air Pollution.
Park, S, and Oh, HS 2017. Spatio-temporal Analysis of ParticulAte Matter Extremes in Seoul: Use of Multiscale Approach. Stochastic Environmental Research and Risk Assessment 1-14.   Seoul Metropolitan Government 2016. A Study on Construction of PM2.5 Inventory and detailed monitoring.
Shaddick, G, Thomas, ML, Green, A, Brauer, M, Donkelaar, A, and Burnett, R 2017. Data Integration Model for Air Quality: A Hierarchical Approach to the Global Estimation of Exposures to Ambient Air Pollution. Journal of the Royal Statistical Society: Series C 66: 1-5.  WHO 2016. WHO Global Urban Ambient Air Pollution.
Wickham, H 2011. ggplot2. Wiley Interdisciplinary Reviews: Computational Statistics 3(2):180-185.  Zhang, Q, Jiang, X, Tong, D, Davis, SJ, Zhao, H, Geng, G, and Ni, R 2017. Transboundary Health Impacts of Transported Global Air Pollution and International Trade,”. Nature 543: 705-718.  
Figure 1.
Boxplots of PM2.5 concentration for the districts in Seoul 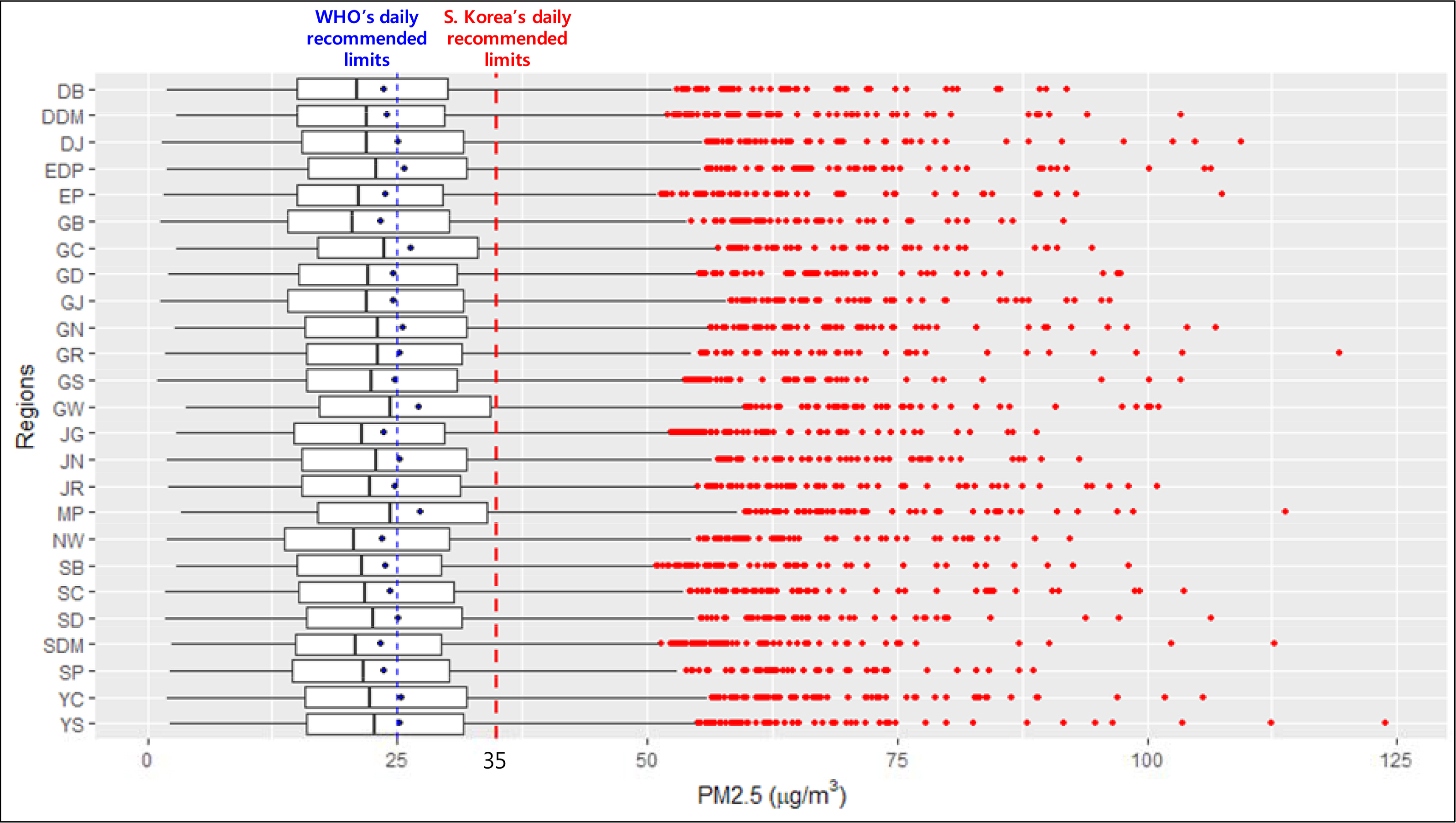
Figure 2.
Analysis procedure of this research 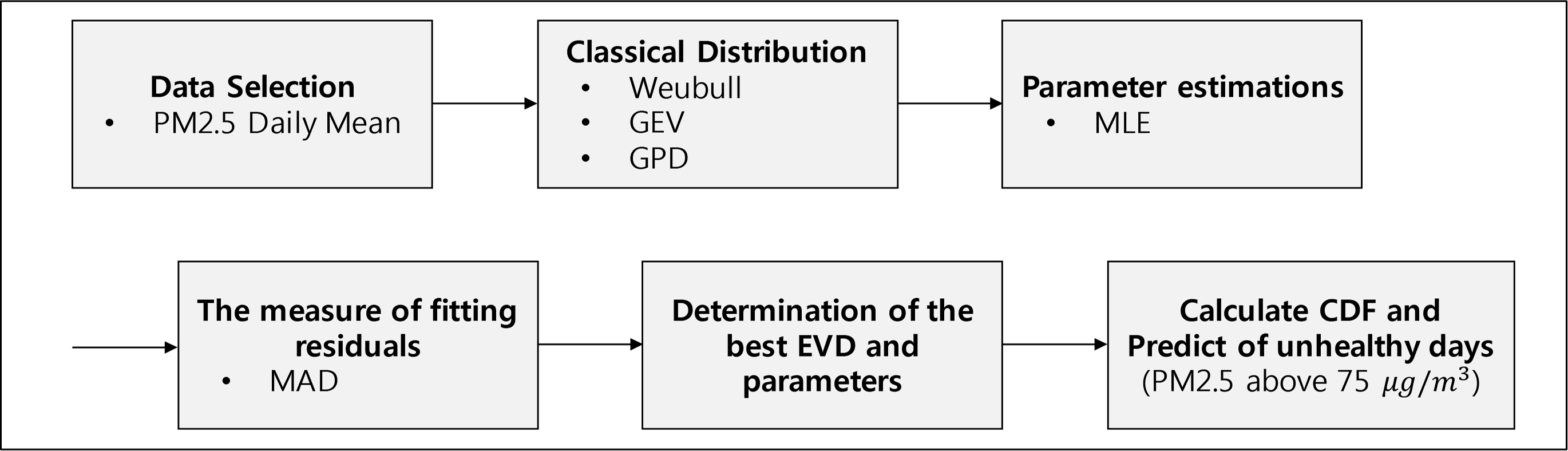
Figure 3.
Diagnostic plots of GEV and GPD fitting for Dong-Jak(DJ) district 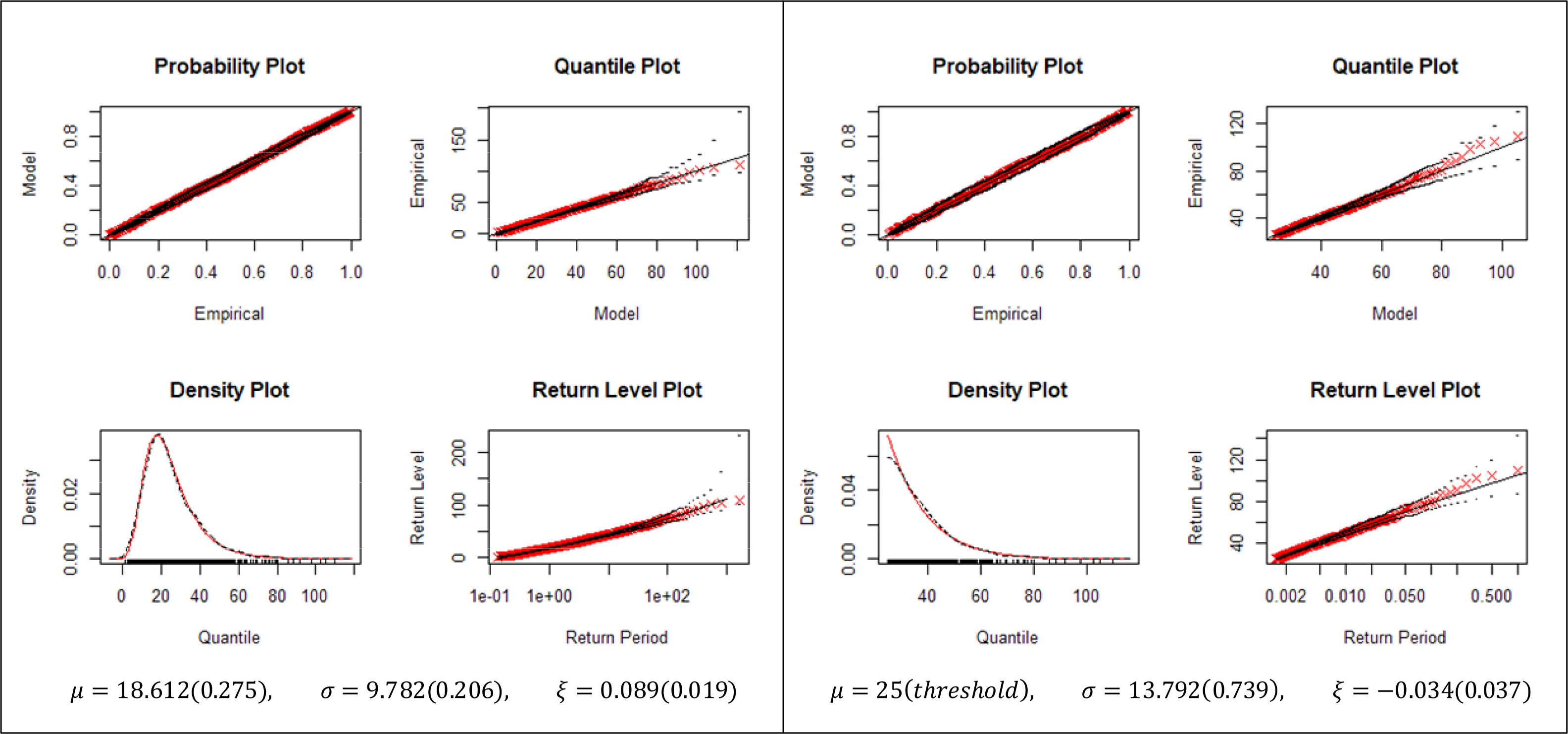
Figure 4.
The residuals and MAD of fitted distributions for Dong-Jak(DJ) district 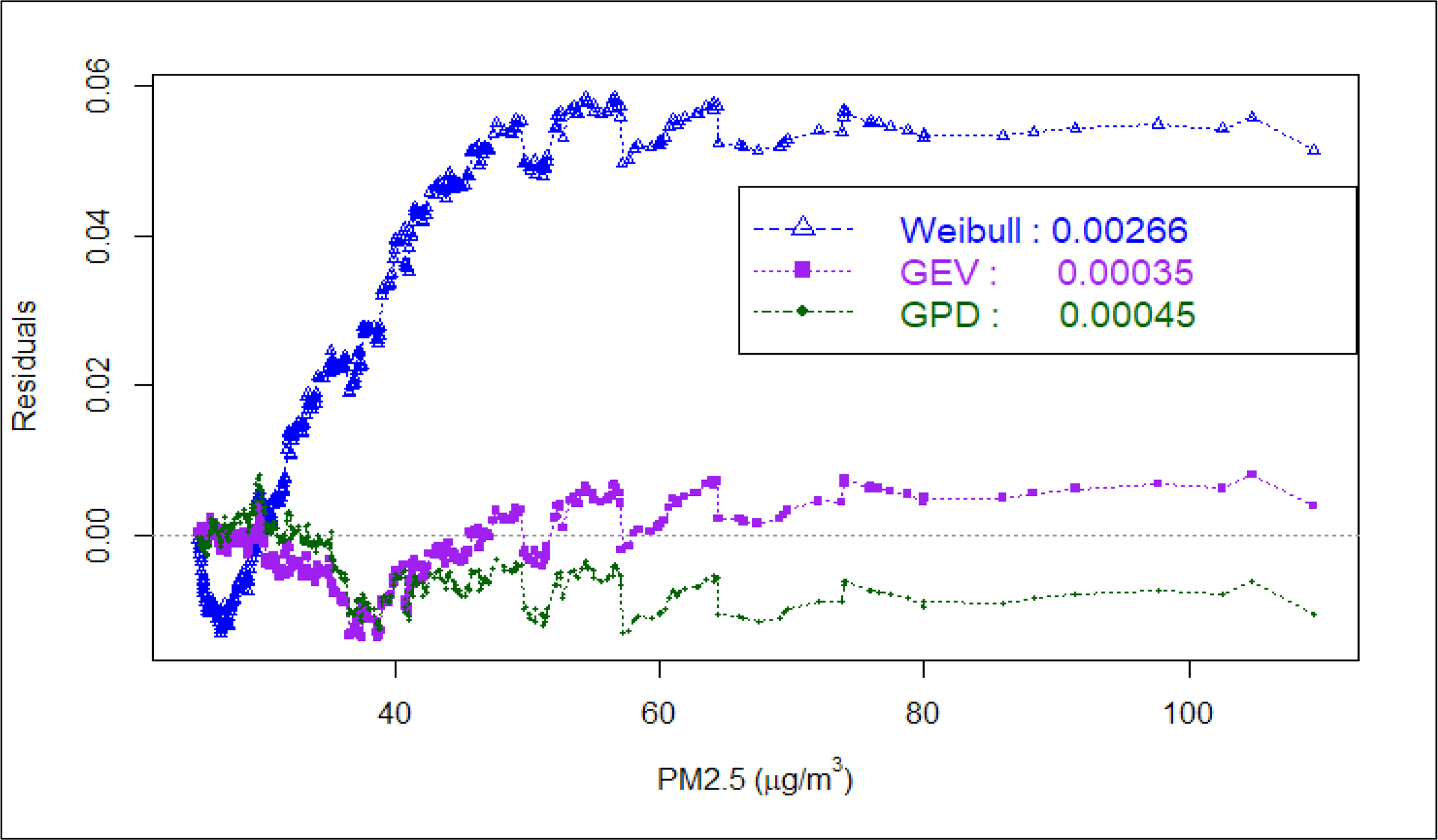
Figure 5.
Return level maps of the PM2.5 concentration classified by districts 
Table 1.
|
Parameters |
n: number of observed data |
σ: scale parameter |
|
μ: location parameter |
λ: shape parameter |
|
|
Acronyms |
CDF: Cumulative Distribution Function |
|
|
EVD: Extreme Value Distribution |
MLE: Maximum Likelihood Estimation |
|
EVT: Extreme Value Theory |
MAD: Mean AbsoluteDeviation |
|
GEV: Generalized Extreme Value |
PDF: Probability Density Function |
|
GPD: Generalized Pareto Distribution |
PM2.5: Particulate matter of diameter less than 2.5 μm
|
|
|
Acronyms for Districts in Seoul |
GN: Gangnam |
GJ: Gwangjin |
DDM:Dongdeamun |
SD: Seongdong |
YS: Yongsan |
|
GD: Gangdong |
GR: Guro |
DJ: Dongjak |
SB: Seongbuk |
EP: Eunpyoeng |
|
GB: Gangbuk |
GC: Geumcheon |
MP:Mapo |
SP: Songpa |
JN: Jongno |
|
GS: Gangseo |
NW: Nowon |
SDM:Seodaemun |
YC: Yangcheon |
JG: Junggu |
|
GW: Gwanak |
DB: Dobong |
SC:Seocho |
EDP: Yeongdeungpo |
JR: Jungnang |
Table 2.
Basic statistics of PM2.5 concentration for each district in Seoul (2014.01∼2018.06)
|
District |
DB |
DDM |
DJ |
EDP |
EP |
GB |
GC |
GD |
GJ |
GN |
GR |
GS |
GW |
|
n |
974 |
910 |
909 |
938 |
996 |
876 |
871 |
968 |
948 |
942 |
936 |
959 |
913 |
|
min |
2 |
3 |
2 |
2 |
2 |
1 |
3 |
2 |
1 |
3 |
2 |
1 |
4 |
|
max |
92 |
103 |
110 |
106 |
108 |
92 |
95 |
97 |
96 |
107 |
119 |
103 |
101 |
|
mean |
24 |
24 |
25 |
26 |
24 |
23 |
26 |
25 |
25 |
26 |
25 |
25 |
27 |
|
sd |
13 |
13 |
14 |
14 |
13 |
14 |
14 |
14 |
15 |
14 |
14 |
13 |
14 |
|
District |
JG |
JN |
JR |
MP |
NW |
SB |
SC |
SD |
SDM |
SP |
YC |
YS |
- |
|
n |
862 |
919 |
991 |
913 |
861 |
925 |
913 |
1005 |
964 |
927 |
887 |
865 |
- |
|
min |
3 |
2 |
2 |
3 |
2 |
3 |
2 |
2 |
3 |
2 |
2 |
2 |
|
max |
89 |
93 |
101 |
114 |
92 |
98 |
104 |
106 |
113 |
89 |
106 |
124 |
|
mean |
24 |
25 |
25 |
27 |
23 |
24 |
24 |
25 |
23 |
24 |
25 |
25 |
|
sd |
13 |
14 |
14 |
15 |
14 |
13 |
14 |
14 |
13 |
13 |
14 |
14 |
Table 3.
The PDF and CDF of fitted distributions
|
Distribution |
Probability Density Function (PDF) |
Cumulative Distribution Function (CDF) |
|
Weibull |
f(x)=(μσ)(xσ)μ−1exp[−(μσ)μ]
|
F(x)=1−exp[−(xσ)μ]
|
|
GEV |
f(x)={exp(−(1+ξx−μσ)−1/ξ), ξ≠0exp(−x−μσ)exp(−exp(−x−μσ)),ξ=0
|
F(x)={(1+ξx−μσ)(−1/ξ)−1exp(−(1+ξx−μσ)−1/ξ),ξ≠0exp[−exp(x−μσ)],ξ=0
|
|
GPD |
f(x)=1σ(1+ξ(x−μ)σ)(−1/ξ−1)
|
F(x)={1−(1+ξ(x−μ)σ)−1/ξ,ξ≠01−exp(−x−μσ),ξ=0
|
|
Parameters |
Location: μ, Scale:σ, Shape: ξ |
Table 4.
Selection of the best model and the MLE for each district
|
District |
Model MAD |
Location (SE) |
Scale (SE) |
Shape (SE) |
District |
Model MAD |
Location (SE) |
Scale (SE) |
Shape (SE) |
|
DB |
GEV 0.00039 |
17.647 (0.265) |
9.489 (0.196) |
0.057 (0.019) |
DDM |
GPD 0.00037 |
25 (NA) |
11.912 (0.691) |
0.01 (0.042) |
|
DJ |
GEV 0.00035 |
18.612 (0.274) |
9.782 (0.206) |
0.089 (0.019) |
EDP |
GEV 0.00044 |
19.246 (0.271) |
9.709 (0.203) |
0.086 (0.019) |
|
EP |
GEV 0.0005 |
17.901 (0.257) |
9.231 (0.191) |
0.071 (0.018) |
GB |
GPD 0.00042 |
30 (NA) |
13.147 (0.899) |
−0.093 (0.047) |
|
GC |
GEV 0.00034 |
20.01 (0.286) |
10.155 (0.211) |
0.047 (0.019) |
GD |
GEV 0.00028 |
18.354 (0.277) |
9.91 (0.207) |
0.057 (0.019) |
|
GJ |
GPD 0.00032 |
30 (NA) |
15.108 (0.974) |
−0.1 (0.045) |
GN |
GEV 0.00021 |
18.927 (0.284) |
10.147 (0.213) |
0.076 (0.019) |
|
GR |
GEV 0.00035 |
19.039 (0.273) |
9.78 (0.202) |
0.055 (0.018) |
GS |
GEV 0.00038 |
18.762 (0.274) |
9.796 (0.202) |
0.04 (0.018) |
|
GW |
GEV 0.00042 |
20.549 (0.285) |
10.187 (0.212) |
0.065 (0.019) |
JG |
GEV 0.00031 |
17.621 (0.264) |
9.34 (0.197) |
0.061 (0.02) |
|
JN |
GPD 0.00036 |
25 (NA) |
13.823 (0.768) |
−0.061 (0.04) |
JR |
GEV 0.00036 |
18.375 (0.277) |
9.917 (0.207) |
0.074 (0.019) |
|
MP |
GPD 0.0003 |
25 (NA) |
14.38 (0.74) |
−0.037 (0.037) |
NW |
GPD 0.00048 |
30 (NA) |
13.189 (0.912) |
−0.066 (0.049) |
|
SB |
GEV 0.00028 |
17.786 (0.254) |
8.994 (0.192) |
0.083 (0.02) |
SC |
GEV 0.00044 |
18.137 (0.268) |
9.632 (0.199) |
0.063 (0.018) |
|
SD |
GEV 0.00026 |
18.767 (0.275) |
9.858 (0.204) |
0.057 (0.019) |
SDM |
GPD 0.00047 |
30 (NA) |
12.038 (0.815) |
−0.031 (0.044) |
|
SP |
GPD 0.00028 |
30 (NA) |
10.513 (0.773) |
0.017 (0.055) |
YC |
GEV 0.00047 |
18.801 (0.28) |
9.907 (0.211) |
0.092 (0.019) |
|
YS |
GEV 0.00029 |
18.972 (0.269) |
9.603 (0.201) |
0.08 (0.019) |
|
- |
Table 5.
Predicted number of unhealthy days (above 75μg/m3 PM2.5) for each district
|
District |
DB |
DDM |
DJ |
EDP |
EP |
GB |
GC |
GD |
GJ |
GN |
GR |
GS |
GW |
|
Actual no. of unhealthy days |
10 |
10 |
15 |
13 |
10 |
8 |
14 |
12 |
14 |
15 |
12 |
8 |
17 |
|
Predicted no. of unhealthy days |
8 |
9 |
15 |
15 |
7 |
6 |
12 |
11 |
12 |
14 |
11 |
9 |
16 |
|
District |
JG |
JN |
JR |
MP |
NW |
SB |
SC |
SD |
SDM |
SP |
YC |
YS |
|
|
Actual no. of unhealthy days |
8 |
14 |
17 |
20 |
12 |
9 |
14 |
13 |
6 |
6 |
16 |
11 |
- |
|
Predicted no. of unhealthy days |
8 |
10 |
13 |
17 |
8 |
9 |
11 |
10 |
7 |
5 |
16 |
11 |
Table 6.
Return levels of the PM2.5 concentration for each district
|
District |
RL (6months) |
RL (1year) |
RL (3years) |
RL (5years) |
District |
RL (6months) |
RL (1year) |
RL (3years) |
RL (5years) |
|
GN |
84(78,91)
|
95(87,104)
|
113(101,128)
|
113(108,140)
|
SDM |
73(68,79)
|
80(74,89)
|
91(83,106)
|
97(87,114) |
|
GD |
78(73,85) |
88(81,97) |
103(94,117) |
103(99,127) |
SC |
77(72,84) |
86(80,96) |
103(93,116) |
103(99,126) |
|
GB |
72(68,78)
|
78(73,87)
|
88(80,100)
|
91(83,107)
|
SD |
78(73,85) |
88(81,97) |
104(94,116) |
104(100,126) |
|
GS |
75(78,92) |
84(78,92) |
97(89,110) |
97(94,118) |
SB |
76(71,83) |
86(79,96) |
103(92,118) |
103(99,129) |
|
GW |
83(78,91) |
94(86,103) |
111(100,125) |
111(107,136) |
SP |
72(67,79)
|
79(73,90)
|
92(81,111)
|
98(85,122) |
|
GJ |
79(75,85) |
86(80,95) |
96(88,109) |
100(91,116) |
YC |
85(79,93)
|
97(88,107)
|
116(104,132)
|
116(111,145)
|
|
GR |
78(73,84) |
87(81,96) |
103(93,115) |
103(99,125) |
EDP |
83(77,90) |
94(86,103) |
110(101,127) |
110(108,139) |
|
GC |
80(75,86) |
89(82,98) |
104(94,117) |
104(100,126) |
YS |
81(75,88) |
102(93,115)
|
108(98,123) |
108(105,135) |
|
NW |
75(70,81) |
81(76,91) |
92(84,106)
|
96(87,114)
|
EP |
76(71,82) |
86(79,94) |
101(92,114) |
101(98,124) |
|
DB |
75(70,81) |
84(78,93) |
97(90,112) |
97(96,121) |
JN |
78(73,85) |
85(79,94) |
96(87,110) |
101(90,118) |
|
DDM |
77(71,84) |
85(78,96) |
99(88,117) |
105(93,128) |
JG |
75(70,82) |
84(77,93) |
97(89,113) |
97(95,122) |
|
DJ |
83(77,91) |
95(87,105)
|
114(102,129)
|
114(109,142)
|
JR |
81(76,89) |
92(84,101) |
110(99,124) |
110(105,135) |
|
MP |
84(79,92) |
92(86,103) |
105(95,122) |
111(99,130) |
Mean |
78.32 |
87.88 |
102.12 |
103.72 |
|
|