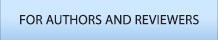본 연구의 대상인 국내 모 발전본부 발전설비 예측진단 시스템은 3가지 부분으로 구성되어 있다. 하나는 운전 정보 시스템으로 발전설비에서 실시간으로 발생하는 운전 정보를 축적하여 데이터베이스화하는 시스템이다. 즉 이는 보다 효율적인 분석을 위하여 그 근간이 되는 데이터를 체계적으로 구축하는 시스템이라고 볼 수 있다. 다음 시스템은 조기 경보 시스템으로, 기 구축된 실시간 데이터를 통하여 학습 과정 등을 통한 머신러닝 기술을 기반으로 하여 설비 고장을 사전에 인지하고, 이에 따른 안정성을 지속 유지하도록 관리를 해주는 시스템이다. 즉 설비 고장에 대한 관리 수행에 직접 연관되어있는 시스템이라 할 수 있다. 마지막으로 성능감시 시스템은 설비의 최적 상태 유지를 위하여 감시, 감독 등의 역할을 담당하는 시스템이다.

따라서 제안되고 발전되어 온 관련 이론을 적용하고, 그 효용성을 검증하며, 설비의 안정성을 확대하고, 고품질의 설비를 유지할 수 있는 부분이 조기 경보 시스템 분야라고 할 수 있다. 본 연구에서 검토하고자 하는 대상도 조기 경보 시스템이며, 현재 이 시스템에서 안전 진단을 위하여 설비에 장착되어있는 감시 센서가 약 4,300여 개에 이른다. 이는 관리 프로세스가 인력에 의존할 수 없음과 더불어 관리 시스템의 자동화 및 효율화가 필수 불가결함을 의미한다.

설비에 장치되어있는 감시 센서에서는 감시 대상의 중요도 및 필요도 수준과 기준에 따라 매초 단위, 매분 단위 또는 매시간 단위의 감시가 진행되며, 감시가 진행되는 과정에서 센서에서 발생한 데이터들은 데이터베이스에 축적되고 학습 과정을 통하여 다시 안전 진단 모형에 활용되는 구조를 지니고 있다. 이러한 감시 센서에서 관리하는 실제 사례 화면은 다음 그림과 같다.

해당 관리 시스템의 적용 방식은 그림에서도 확인할 수 있듯이 목표치에 대한 관리로만 의존이 되고 있다. 한편 목표치 이외에 목표치의 편차를 관리하는 방안 중 하나인 Constrained Bayes 추정량에 대한 적용 방식이 제조업뿐만 아니라 금융권에 적용하는 방안이 제시되기도 하였다(Kim and Kim 2014; Kim and Kim 2015). 하지만 설비장비에서 목표치의 편차를 고려하여 해당 분포에 근사시키고자 하는 이론은 설비 장비의 안전 관리 시스템에서는 유효한 접근 방식이라고 하기에는 부적절할 수도 있다. 이는 관리의 목적이 목표치에 근사하는지가 주된 목적이기 때문이며, 따라서 이러한 추정방식 이외의 접근 방식을 모색할 필요가 있다.

그동안의 대부분 연구를 보면, 목표치를 잘 예측하고 오차를 최소화하는 분석 방식들이 다양하게 제안되고 적용되어 발전해 오고 있지만, 관심의 대상은 오로지 목표치에만 치중되어왔다. 본 연구의 대상인 해당 조기 경보 시스템도 기존에 활용되어오던 통계적 모형 방식에서 머신러닝 기법을 적용하여 대량으로 생산되는 데이터의 활용을 극대화하는 방향의 시도가 이루어지기는 하였지만, 이 또한 적용 기법의 고도화가 이루어진 것일 뿐, 목표치의 대상에만 관심을 가지는 패러다임에서의 변화는 없다고 할 수 있겠다.

따라서 본 연구의 다음 장에서는, 목표치 이외에 목표치 추정을 통하여 발생하는 오차항을 이용하여 관심의 대상을 확장하고, 이에 대한 통제를 통하여 보다 효율적인 안정성을 확보하고자 하는 방안을 소개하고자 한다. 다음 절에서는 러닝 기법 중 연구 대상이 되는 시스템에 적합하게 적용할 수 있는 머신러닝 기법 중 하나인 Support Vector machine 방식과 딥러닝 기법 중 하나인 Multi Layer Perception 방식을 소개한다.

본 연구에서 예측 모형으로 적용하는 방식은 머신러닝 기법 증 연속형 변수의 예측에 가장 많이 활용되는 방식인 SVM(Support Vector Machine)과 딥러닝 기법의 중 신경망의 개념을 이용하는 MLP(Multi Layer Perception) 방식이다. 본 연구에서는 어떠한 러닝 기법이 우수한지를 검증하거나 그에 대한 효용성을 검증하는 것이 아니므로, 이에 대한 자세한 설명은 생략하고, 개괄적인 적용 방식의 개념만을 소개하기로 한다.

SVM은 분류 및 회귀에 주로 사용되는 기계 학습 방법으로, 고차원 또는 무한 차원의 공간에서 초평면을 찾아 이를 이용하는 비모수적 지도학습기법이다. SVM은 1992년 Vapnik에 의해 최초로 정립되었고, 1997년 Vapnik, Steven Golowich 그리고 Alex Smola가 회귀를 위한 SVM 버전으로 SVR(support Vector Regression)을 제안했다. SVR은 SVM의 가장 일반적인 응용 프로그램의 형태로, 회귀 및 함수의 추정을 위한 서포트 벡터의 기본 아이디어는 Smola and Schölkopf(1998)에 제시되었다. 연속형 자료로 측정하는 발전설비의 예측진단을 위한 모니터링에 사용할 수 있는 ε-SVR(epsilon-support vector regression)은 Basak(2007)이 다음과 같이 정리하였다.

모형 구축을 위한 훈련 자료는 예측변수 x_i와 목표변수 y_i를 포함하며, ℵ를 R^d와 같은 입력 패턴의 공간이라고 가정하면, 훈련 자료는 {(x₁, y₁),...,(x_l,y_l)}⊂ℵ×R로 가정할 수 있다. ε-SVR은 모든 훈련 자료에 대하여 ε보다 크지 않은 값만큼 y_i에서 벗어나며, 동시에 최대로 평탄한 함수 f(x)를 구하는 것이 목적이다. 선형 함수 f는 다음과 같다.

여기서 <.,.>은 스칼라곱(scalar product)이며, 이 함수가 평탄하도록 최소 놈 값 ∥w∥²을 갖는 f(x)를 구하는 것은 다음을 최소화하는 컨벡스 최적화(convex optimization) 문제로 볼 수 있다.

여기에는 모든 찬자가 ε보다 작은 값을 갖는다는 조건이 적용되며, 이를 수식으로 나타내면 다음과 같다.

따라서 본 연구에서는 SVM 방식은 최적의 구간(kernel)과 설정된 구간에서 적정 함수를 적용하여 모형 적합과정에서 발생하는 오차를 최소화하는 일련의 과정을 반복 수행하였으며, 자세한 내용은 연구 분석 결과에 별도로 설명하였다. 이러한 모형의 적용방식은 의료 분야에서 암에 대한 예측진단을 하는 도구로 제안하는 연구 결과가 제시되었으며(Kourou et al 2015; Cruz and Wisher 2006), 금융 분야에서 온라인 가격 결정을 하는 모형으로 활용하는 방안에 대한 연구에도 활용되었다.(Oliver 1996). 즉 이는 예측진단에 있어 본 연구에서 활용하고자 하는 모형에 적합함을 확인할 수 있다. 머신러닝 기법이 가지는 과다추정(over-fitting)의 문제는 이론적인 통계적 이슈에 대한 논의를 별개로 함을 밝혀 둔다.

신경망 또는 인공신경망(artificial neural network) 기법은 인간의 뇌신경계를 모방하여 수학적 모델링 기법으로 인공적인 지능을 만드는 것이다(Hagan et al., 1996). 최초의 모델은 McCulloch and Pitts(1994)에 의해 제시되었으며, 이후 단층신경망의 XOR 문제를 극복한 역전파(back propagation) 알고리즘이 적용된 다층신경망 방식에 관한 연구 결과가 제시되었다(Hinton 1986; Picton 1994)

인공신경망 구조는 한 개의 입력층(input layer), 한 개 이상의 은닉층(hidden layer) 그리고 한 개의 출력층(output layer)으로 구성된 다층신경망(multi-layer perceptron neural network)으로 형성되어 있으며, 각각의 층(layer)은 노드들로 이루어지며, 각 노드들은 연결 가중치(weight)가 부여된 선으로 연결되어 있다. 개별 노드는 이전 단계의 출력값을 다시 입력값으로 받아 활성함수를 통해 출력값을 산출하며, 인공신경망은 출력값과 오차를 줄이는 방법으로 오차 역전파를 사용, 연결가중치를 조정하는 방법이다. 반복적으로 오차가 작아지도록 노드들의 연결가중치를 조절하는 과정을 수식으로 나타내면 다음과 같다.

여기서 e는 오차를 의미한다. MLP(multi-layer perceptron) 신경망의 경우 입력층의 각 노드에는 설명변수가 입력되며, 은닉층에 위치한 노드들의 출력 벡터는 다음과 같은 함수로 계산된다.

출력층의 경우 노드의 출력값은 다음과 같다.

여기서 z=w^'O_h+w₀이며 w는 가중치 벡터를 의미한다. 결과적으로 출력층의 값 O_n은 은닉층 노드의 출력 벡터 O_h의 가중치 값의 결합으로 구성되기 때문에 다층퍼셉트론 인공신경망은 여러 개의 로지스틱 함수를 선형(linear) 결합한 비선형(non-linear) 판별함수를 가지게 된다. 이러한 인공신경망 기법은 복잡한 비선형적 관계를 병렬적으로 분석할 수 있으며, 데이터 학습(machine learning)을 통한 예측 및 일반화의 능력이 뛰어나다는 연구 결과가 제시되었다(Basheer and Hajmeer, 2000). 따라서 본 연구의 대상이 되는 예측 진단의 비선형적 관계를 규명하는 것에 적합한 방법이라 할 수 있겠다.

예측진단 시스템에서 관리 센서에서 실시간으로 생성되는 포인트는 4,000여 개에 이른다. 이 중에서 관리 목표치의 단위가 상이한 2가지의 대표적인 센서를 선택하여 분석 대상으로 선정하였다. 대상을 선정한 이유는 2개의 관리 시스템에서 생성되는 데이터의 운전 범위와 예측오차, 관리 범위가 구체적으로 제시되어 있기 때문이다.

선정된 첫 번째 설비는 급수 가열기에서 설치된 센서에서 생성되는 데이터로 운전 범위는 240~245mm, 예측오차는 +/- 2mm이며, 관리 범위는 양의 방향으로는 10mm, 음의 방향으로는 20mm로 관리되는 설비이다. 데이터 생성주기는 매시간 단위로 매일 24개의 데이터가 생성되어 관리되는 과정이다.

다른 설비는 급수의 압력을 관리하는 설비에 설치되어있는 센서로 운전 범위는 24~27kg/cm2, 예측오차는 +/- 0.3kg/cm2 이며, 관리 범위는 양의 방향으로는 1kg/cm2, 음의 방향으로는 2kg/cm2이다. 이는 첫 번째 대상에 비하여 상대적인 단위가 작으며 예측오차와 관리 범위도 이에 비례하여 낮은 수준에서 관리되는 설비이며, 이 설비도 하루에 24번 매시간별로 생성되는 데이터를 기준으로 관리되고 있다.

연구에 활용된 데이터는 분석 기간 중 결측치가 발생하지 않도록 설정하여 2019년 2월 5일 23시부터 4월 24일 16시까지 생성된 데이터를 기준으로 진행되었으며, 1일, 24개, 약 3개월 기간 동안 생성된 데이터로 분석 대상에 활용된 데이터의 수는 장비별로 1,866개이며, 이중 4월 9일 23시까지 생성된 1,513개의 데이터는 훈련용 데이터로 활용되며, 이후 발생된 353개의 데이터는 검증용 데이터로 활용하였다. 이를 그림으로 표현하면 다음과 같다.

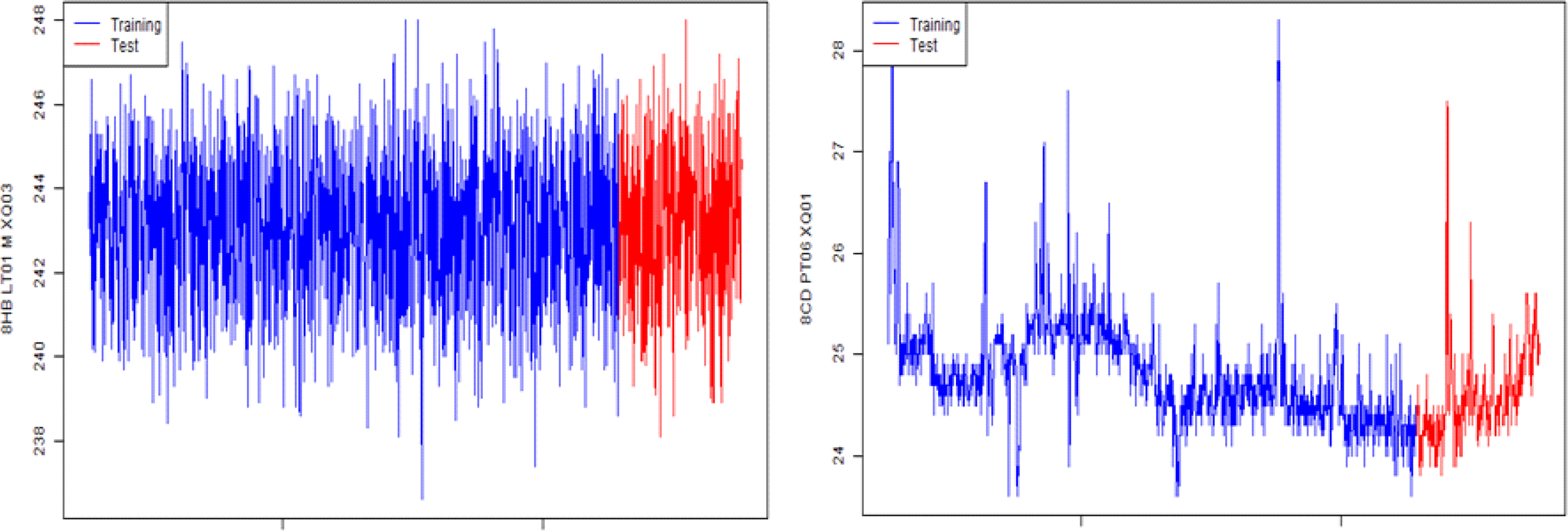
이렇게 관리 목표치의 단위와 관리 수준이 상이한 2개의 센서를 연구 대상으로 선정한 후, 이와 연관성이 높은 센서를 탐색하게 된다. 이렇게 연관성이 높게 나타난 센서는 공동의 관리 대상군으로 판단할 수 있기 때문에, 이렇게 선정된 변수를 이용하여 시간의 흐름별 모형의 설명변수로 활용하게 된다. 러닝 기법을 적용하기 위하여서는 훈련 데이터와 검증 데이터를 분류하여 적용하여야 하므로 연관성을 판단할 때에도 모형에 적용되는 훈련 데이터를 기준으로 검토되었다. 아래의 그림은 각각의 설비별로 연관성이 높은 변수를 발굴하여 그 정도를 확인한 결과를 도식화한 내용으로 양의 연관성을 가지기도 하며, 음의 연관성을 가지기도 하므로, 절대값 기준으로 상관계수가 0.8을 상회하는 변수를 선정하였다.

이와 같이, 선정된 목표 설비와 관련 설비를 토대로 2가지 모형이 본 연구에서 진행되게 된다. 머신러닝과 딥러닝 기법 중 본 연구에 적용하기 타당한 2가지 방식이 적용되며, 훈련 데이터를 통하여 모형이 수립되고, 검증 데이터를 통하여 예측값을 산출한다, 이후 예측값과 실제 값의 차이로 나타나는 오차항에 대하여 특수한 상황을 가정한 시뮬레이션을 적용하고 이에 대한 진단 효과를 확인하게 된다. 검증 방안에 대한 자세한 설명은 다음 절에서 다룬다.

지속적이면서도 안정적인 시스템 운영을 위한 개선 방안으로의 연구는 2가지를 통하여 진행한다. 한 가지는 분석모형에 있어서 보다 고도화된 기술을 적용하는 방식으로의 접근이고, 다른 한 가지는 분석 대상을 기존의 목표치에만 의존하는 것에서 벗어나 예측값과 실제 값의 차이로 나타나는 오차항을 관리 대상에 포함 시켜 보다 민감하게 위험 진단을 파악하는 방안을 제시하는 것이다. 분석 모형의 고도화에 적용하는 방식은 앞 장에서 이론적 근거를 제시하였기에, 이 장에서는 두 번째 제안 방식인 오차항을 관리 대상으로 적용하는 방안에 대하여 자세히 설명하기로 한다.

분석 대상의 데이터는 모두 안전 관리 상태를 유지하고 있는 상태이기 때문에, 매우 사소한 특정 패턴이 발생하는 상황을 가정하여 시뮬레이션을 진행하고, 이를 현 안전 시스템에서 감지하는지의 여부와 본 연구에서 제안하는 방식이 어떻게 민감하게 반응하며 이상 상황을 조기에 감지하는지를 비교함으로써 그 유효성을 입증하고자 한다.

이를 위하여 발생된 오차항에 특정 분포를 가정한 매우 작은 수준의 사건이 지속 발생함을 가정한다. 본 연구에서는 각각의 관리 시점별로 정규 분포에서 평균 0.005 수준과 분산 0.005 수준을 가정한 오차를 지속적으로 발생하여 매 시점에서 실제 발생한 오차에 추가적으로 발생한 수정 오차항으로의 상황을 가정한다. 추가적으로 발생한다고 가정한 잡음(noise)은 모델 검증이 이루어지는 기간의 중간 시점에서 발생하는 것으로 가정하였다. 이를 수식으로 표현하면 다음과 같이 나타낼 수 있다.

분산이 매우 작은 수준이기에 대부분 0.005를 중심으로 사소한 수준의 양의 오차가 지속적으로 발생한다는 상황을 가정한 것으로 이해할 수 있다. 즉 특정 사건으로 오차가 한 방향의 패턴이 사소한 수준으로 발생한다는 상황을 가정한 것이며, 이러한 상황에서 현재의 안전 진단 시스템과 본 연구에서 제안하는 안전 진단 시스템에서의 위험 진단 수준 및 민감도를 검증하여 주요한 설비의 안전 진단 시스템의 보다 효율적인 방안을 제시하고자 한다.

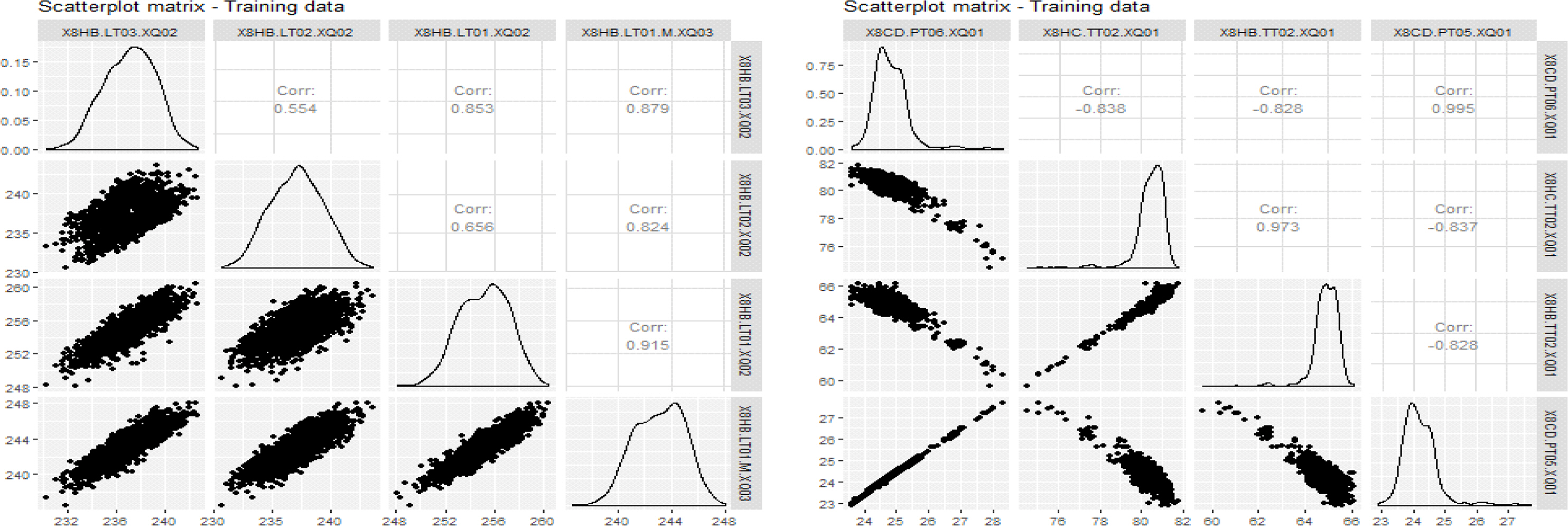
분석 진행은 1차적으로 2개의 설비에서 생산된 데이터를 기준으로 2개의 모형을 적용하며, 적용되는 모형은 SVM(Support Vector Machine)과 MLP(Multi Layer Perception)이다. 모형의 적용은 특정 시점을 기준 이전의 데이터는 훈련용 데이터로 모형을 적합화 하는데 사용하며, 특정 시점 이후 데이터는 모델의 검증 데이터로 활용하게 된다. 첫 번째 설비와 두 번째 설비에 SVM 모형과 MLP 모형을 검증용 데이터에 적용한 분석 결과는 다음 그림과 같으며, 실제 값과 유사한 수준으로 예측되는 것을 확인할 수 있었다. 첫 번째 설비에서 SVM 모형의 RMSE(Root Mean Square Error;평균 제곱근 오차)수준은 0.3551로 MLP 모형의 RMSE는 0.3578로 SVM 모형의 적합도가 다소 양호하게 나타났으며, 두 번째 설비에서는 SVM 모형의 RMSE수준이 0.0606으로, MLP 모형의 RMSE이 0.0570으로, MLP 모형의 적합도가 다소 양호하게 나타났으나, 두 설비 모두 머신 러닝 방식과 딥러닝 방식의 적합도는 대동소이한 것으로 파악되었다.

이 후 검증 데이터의 중간 시점에 일정 수준으로 발생하는 오차의 패턴을 추가하여 시뮬레이션을 진행하게 된다. 이는 장비에 일정 패턴으로 발생 가능한 이상 징후를 가정한 것이며, 이렇게 설정된 특정 오차가 지속 발생한다는 가정하에서 각각의 설비가 현재 위험을 진단하는 방식에서 반응하는 수준과 오차를 관리 대상으로 적용하는 경우에 위험을 진단하는 방식의 반응 수준을 비교하는 분석을 진행하게 된다.

본 연구에서 분석은 R(3.6.1)로 진행하였으며, SVM은 {e1071} 패키지 버전 1.7-1, MLP는 {RSNNS} 패키지 버전 0.4-12를 사용하였다. 두 모형에 대한 매개 변수의 조율은 훈련 자료에서 10-중첩 교차타탕법(10-fold cross validation)을 적용한 RMSE가 가장 낮은 모형을 최적 모형으로 결정하였다. SVM의 타입은 “eps-regression”으로 가우시안 RBF 커널을 사용하고, 매개 변수는 조율을 통하여 ε=0.1, C=100, γ=0.01을 최적 모형으로 결정하였다. MLP는 2개의 은닉층을 가지는 구조로 고정하고 활성화 함수는 시그모이드(sigmoid) 함수를 사용하였다. 각 은닉층 노드의 수는 조율을 통하여 10-10을 최적 모형으로 결정하였다.

특정 시점 이후로 일정 패턴으로 발생하는 오차를 반영하여 현재 운영 중인 예측진단 시스템에서의 위험 진단 여부를 확인하고, 오차항을 별도로 관리 대상으로 선정하여 위험 진단 여부를 비교 분석하였다. 위험 진단 판단의 기준은 현재 운영 중인 시스템의 경우는 기존에 제시된 관리 범위를 그 기준으로 설정하였으며, 오차항에 대한 위험 진단은 새롭게 적용되는 방식으로 그 기준이 존재하지 않는 바, 품질 관리 분야에서 가장 많이 사용되는 Cusum, EWMA와 Run Rules 방식 3가지를 적용하여 판단 기준으로 설정하였다.

아주 사소한 수준이지만, 일정 패턴을 가지는 이상 징후가 계속 발생한다는 가정하에서, 현재 운영 중인 시스템에서는 목표치와의 차이만을 고려하는 방식이기에 검증 기간 내에 어떠한 위험 감지를 하지 못하였다. 이는 위험 관리에 있어 목표 수준만을 관리하는 방안이 내포하는 문제점으로 인식될 수 있으며, 안전성이 최우선으로 간주되는 특정 설비에 있어 추가적인 관리 대안이 필요함을 의미한다.

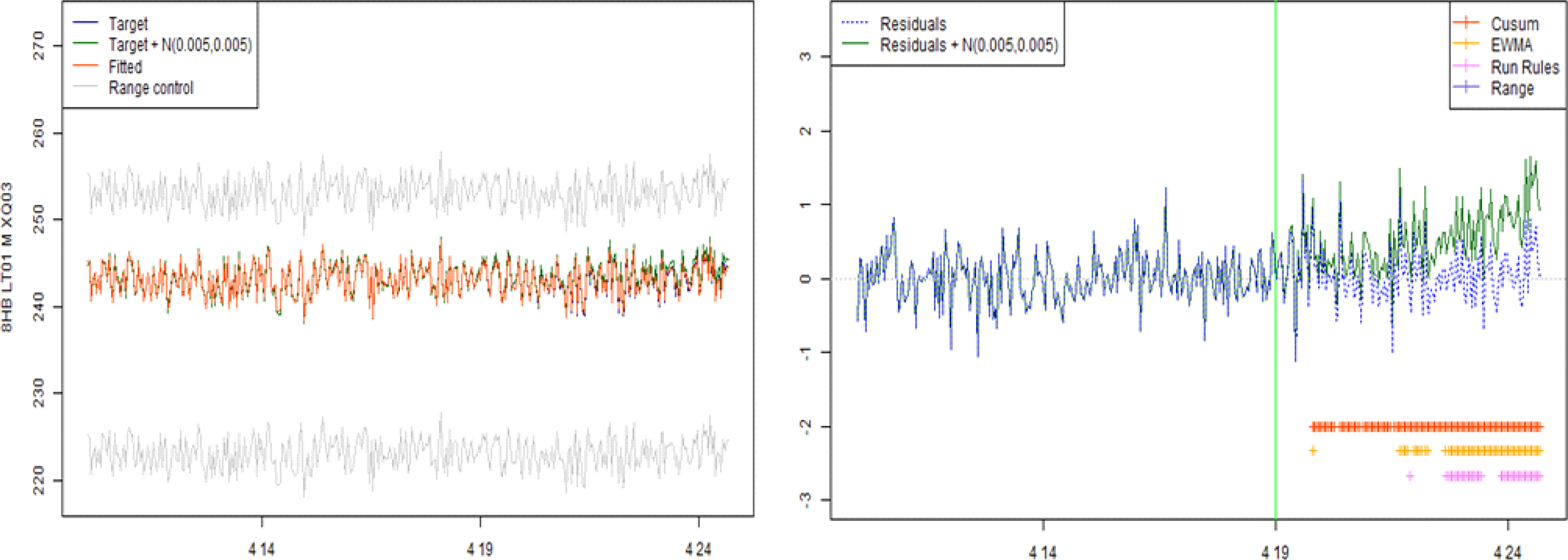
오차항을 관리 대상으로 진행한 이상 징후 분석 결과에서는, 판단 방식에 있어 위험을 진단하는 시점과 위험 수준이라고 판단하는 경우의 수에 다소 차이가 있기는 하나, 일정 패턴의 오차항을 추가한 시점에서 크게 떨어지지 않는 시점에 위험을 조기에 진단하는 분석 결과와 다수의 시점에서 위험 수준이라고 판단하는 분석 결과를 나타냈다. 다음 그림은 첫 번째 설비에서 현재 방식과 제안방식의 위험 진단 여부를 비교한 그림이다.

위의 그림에서 확인할 수 있듯이 기존의 방식에서는 위험 진단이 없는 관리 수준으로 지속 예측하고 있으나, 오차항을 관리하는 제안방식에서는 이상 징후를 조기에 감지하고 있음을 확인할 수 있다. 오른쪽 그림 아래에 판단 방식별로 위험을 인지한다는 것으로 참고로 표현하였다. 위의 진단 결과를 설비별, 모형별, 판단 방식별로 정리한 결과를 다음의 표로 요약하였다.

처음 위험을 감지하는 시점은 판단 방식에서 차이가 있기는 하나, 하루 24개의 포인트를 감지하는 현 설비 기준으로 2일(일별 24개 감지)에서 4일 이후 시점에서 이상 징후를 판단하는 것으로 나타났으며, 6일간의 관리 기간에 발생하는 144개 시점의 대부분에서 이상 징후가 있음을 판단하였다. 이는 본 연구에서 제시하는 오차항 관리 방식이 가지는 민감성을 증명하는 것이며, 보다 적극적이고 보수적인 관리가 필요한 설비에 고려할 수 있는 방식임을 의미한다고 할 수 있다.